2. Биномиальное распределение дсв
ДСВ описывается
биномиальным распределением, если
существует событие А,
для которого известны вероятности его
появления и не появления соответственно
,
(далее
и
),
и для этого события проводится
независимых испытаний, то вероятность
того, что из них
раз произойдет событие А
равна
.
Здесь
-
число сочетаний из
по
,
и рассчитывается по формуле
.
Операция
называется факториал, и представляет
произведение всех целых чисел от 1 до
.
Например,
.
Замечание.
Примем без доказательства, что
=1.
Математическое ожидание для биномиального распределения вычисляется по формуле
.
Дисперсия:
.
Среднеквадратичное отклонение:
.
Пример 2.
Вероятность попадания для стрелка постоянна, и равна 0,6. С какой вероятностью при 5 выстрелах он поразит мишень не менее 3-х раз; какое среднее количество попаданий?
Решение.
Запишем данные:
;
;
;
.
Условие поразить мишень не менее 3-х раз представляет собой сложное событие, при котором количество попаданий может быть 3, 4 или 5. Значит, вероятность такого события равна
Или в терминах биномиального распределения:
.
Среднее число попаданий есть
.
3. Гипергеометрическое распределение дсв
Для применения
этого распределения нужно наличие
объектов, из которых
принадлежит
к 1-му типу, а остальные
- ко 2-му. Далее из
объектов извлекаются наугад и безвозвратно
объектов (
).
Требуется определить вероятность того,
что из этих
объектов,
-
принадлежит к объектам типа
(
).
Тогда такая вероятность определяется
по формуле
.
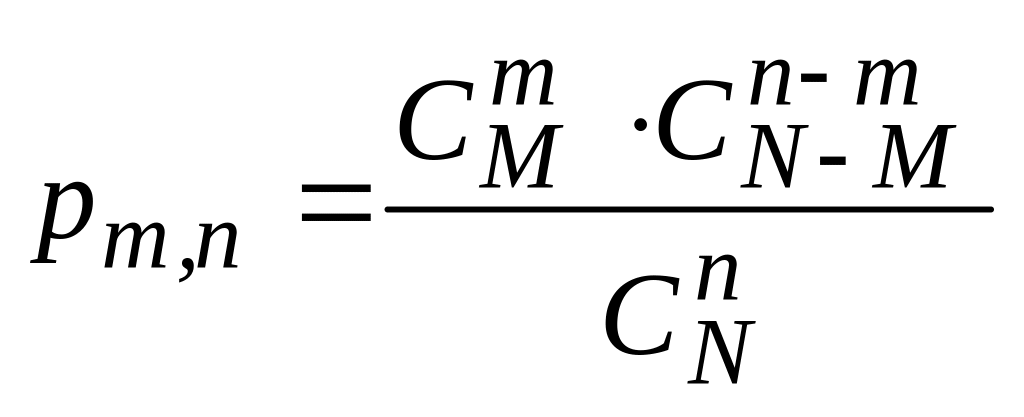Величины , и вычисляются по общим формулам раздела III.1.
Пример 3.
Среди 15 деталей имеется 6 бракованных. Какова вероятность, что при случайном безвозвратном извлечении 3-х деталей, из них будет не менее 2-х годных? Найти среднее количество годных деталей в такой выборке.
Решение.
Запишем данные:
;
;
;
.
Действительно, условие «не менее 2-х» есть сложное событие:
.
Или в терминах гипергеометрического распределения:
.
.
.
Итак,
.
Для нахождения нужно найти все остальные вероятности:
;
.
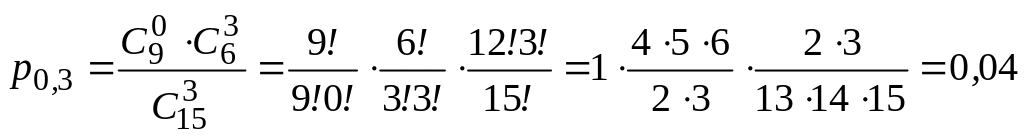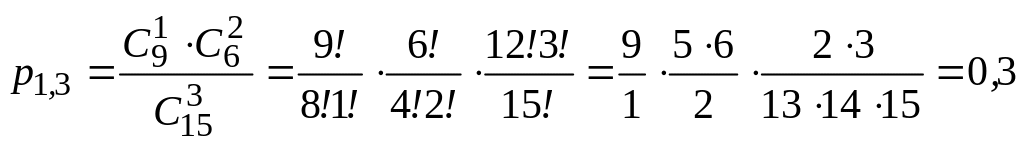Произведем проверку:
.
Найдем
.
Задачи к п. III
Характеристики и параметры ДСВ
Вероятность бракованной детали равна 0,4. Найти функцию распределения
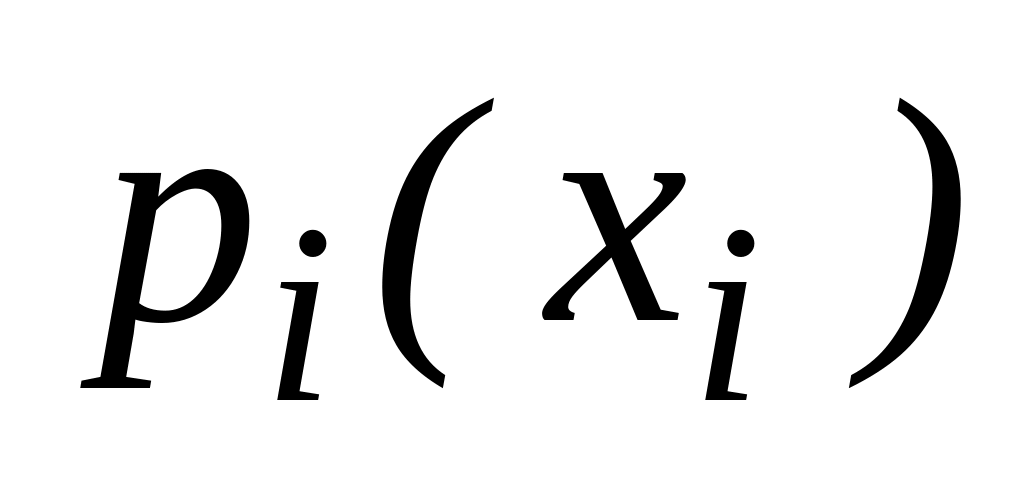при случайной выборке из 3-х деталей.
Найти среднее ожидаемое значение и
среднеквадратичное отклонение.Вероятность попадания стрелка равна 0,6. Какова вероятность того, что при 4 выстрелах он поразит мишень не менее 2-х раз?
Вероятности попаданий трех стрелков соответственно равны 0,4, 0,5 и 0,7. Какова вероятность не менее 2-х попаданий при одном залпе?
Какова вероятность, что при 3-х подбрасываниях кубика хотя бы 2 раза выпадет «2» или «3»?
Вероятность попадания стрелка равна 0,45. Сколько выстрелов он должен сделать, чтобы поразить мишень с вероятностью 0,9 хотя бы один раз?
Известно, что 15 % деталей – бракованных. Какова вероятность, что при извлечении 6 деталей среди них окажется не более 2-х бракованных?
Вероятность поражения мишени для первого стрелка равна 0,8, а для второго неизвестна. Известно, что вероятность при двух залпах поразить мишень по одному разу равна 0,36. Найти вероятность попадания второго стрелка.
Вероятности попаданий двух стрелков относятся как 2:3. Определить величины вероятностей, если известно, что вероятность 1 попадания при залпе равна 0,5.
В урне находятся 10 белых и 7 черных шаров, при этом наугад извлекаются 3 шара. Рассчитать вероятности для всевозможного количества белых шаров среди вытащенных.
В папке имеется 15 файлов размером порядка 0,1 Мб и 6 файлов размером порядка 2 Мб. Какова вероятность того, что 3 наугад взятых файла будут иметь объем не более 3,5 Мб; не менее 1 Мб?
Какова вероятность, что при извлечении 4-х бочонков при игре в лото не менее 3-х будут принадлежать к одному десятку?
Каков риск выше: при вытаскивании двух тузов из пяти карт, или трех тузов из десяти карт?
В урне находится 8 белых шаров и 6 черных. Из нее наугад извлекают 3 шара, а затем из этих шаров – еще один. Какова вероятность, что этот шар окажется белым?
В одной урне 10 белых и 8 черных шаров, в другой – 4 белых и 6 черных. Из каждой урны вытаскивают по 2 шара и кладут в другую урну. Какова вероятность, что при этом в урнах изменятся соотношения белых и черных шаров?
Имеется 12 годных и 10 бракованных деталей. Из них сначала выбирают 3 детали, затем из этих 3-х выбирают одну. Какова вероятность, что это будет годная деталь?
В урне находится 15 белых шаров и 5 черных. Найти кривую распределения для вероятности количества белых, если производится безвозвратная выборка из трех шаров. Найти среднее ожидаемое значение и среднеквадратичное отклонение.
В урне находится 10 шаров с номером «1» и 15 шаров с номером «3». Найти кривую распределения для суммы цифр, если производится бесповторная выборка 3 шаров. Найти среднее ожидаемое значение, и закон распределения.
Найти кривую распределения для количества гербов при подбрасывании 6-ти монеток. Рассчитать закон распределения.
Известно, что вероятность в интервале от 2 до 6 пропорциональна случайной величине
.
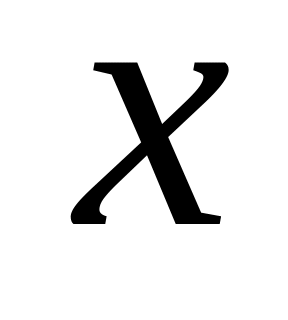Найти кривую распределения, закон
распределения, величины
и
.Вероятности попаданий стрелков равны 0,8; 0,4; 0,65. Найти кривую распределения для количества попаданий, а также среднее ожидаемое значение попаданий при одном залпе.
Вероятность в интервале от -4 до 6 пропорциональна квадрату случайной величины. Найти кривую распределения, закон распределения, величины и .А
3
3,5
В
2,2
4,8
Рi
0,3
0,7
Рi
0,4
0,6
Точки А и В, расположенные на оси Ox, имеют заданные кривые распределения вероятностей (см. таблицу). Найти среднюю длину отрезка АВ.
В партии имеется 25% бракованных деталей. Сколько раз нужно выбирать деталь, чтобы с вероятностью 0,95 достать хотя бы одну годную деталь?
Функция распределения имеет вид:
Найти плотность распределения, математическое ожидание и дисперсию. Найти вероятность, что случайная величина будет лежать в интервале (2,5;5).
Задана плотность распределения непрерывной случайной величины:
Найти функцию распределения, математическое ожидание и дисперсию.
Случайная величина X задана плотностью распределения в интервале
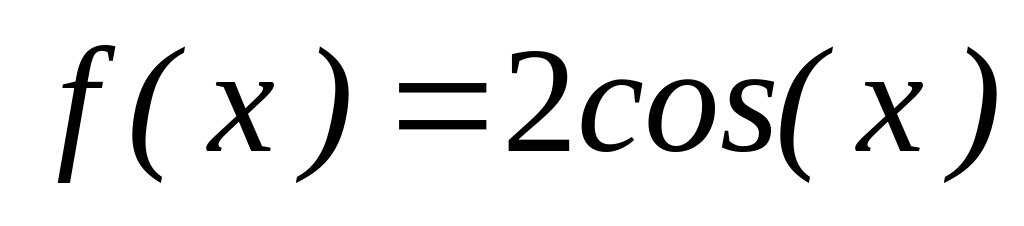на
,
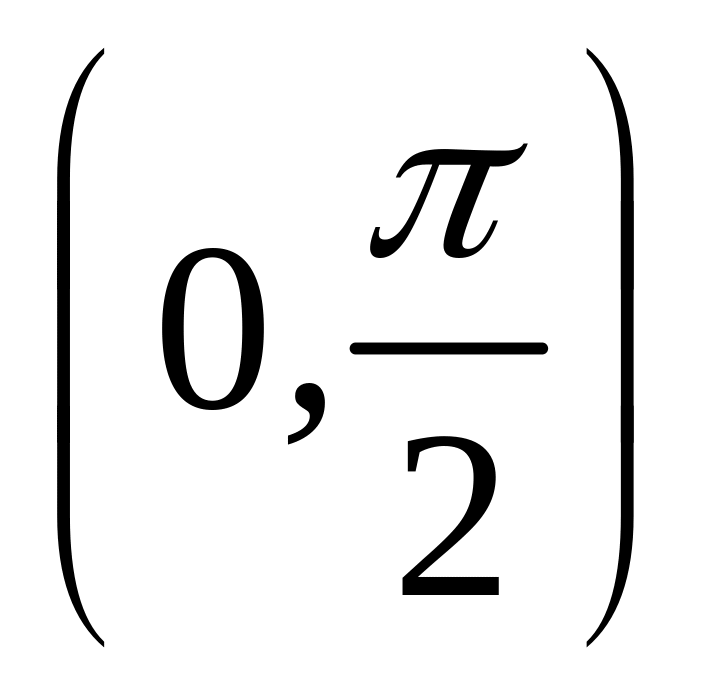вне этого интервала плотность равна
нулю.
Найти функцию распределения, математическое ожидание и дисперсию.