VII. Регрессионный анализ

1. Понятие регрессии, основные виды уравнений регрессии

Понятие регрессии (см. п.VI.5) и корреляции связаны между собой, но имеется и важное отличие. Коэффициент корреляции дает оценку силе связи между двумя статистическими величинами, а в регрессионном анализе исследуется форма связи.

Пусть имеются две статистические величины и . Если для них удается найти функциональную взаимосвязь

,

то такая функциональная зависимость называется уравнением регрессии.

В общем случае может быть несколько статистических величин , и тогда уравнение можно записать так

.

Очевидно, что если известна функция от одной из величин, например , то всегда можно найти функцию от любой другой величины.

Пусть задана функция

.

Выразим ее как функцию и :

; .

По этой причине (только лишь для упрощения выкладок), будем выражать через ту случайную величину, относительно которой будем искать зависимость.

Если уравнение регрессии удалось получить, то это существенно упрощает анализ многомерных статистических объектов, а также прогнозирование его поведения в заданных условиях.

Построение уравнения регрессии предполагает решение трех основных задач:

1) Выбор независимых переменных, оказывающих существенное влияние на зависимую величину.

2) Определение вида уравнения регрессии.

3) Построение уравнения регрессии, то есть определение параметров (коэффициентов) уравнения.

Наиболее распространенными видами уравнений регрессии являются:

- линейное однофакторное;

- линейное многофакторное;

- полиномиальное;

- гиперболическое;

- степенное.

Следует отметить, что степенное уравнение регрессии может быть легко сведено к линейному уравнению с помощью операции логарифмирования:

.

Теперь переобозначив переменные, получим уравнение регрессии

,

которое является линейным. Определив для новых статистических величин искомые коэффициенты, вернемся к исходному коэффициенту .

2. Метод наименьших квадратов для вычисления уравнений регрессии

Метод наименьших квадратов (МНК) является универсальным способом отыскания коэффициентов уравнений регрессии.

Исследуя метод МНК, ограничимся только однофакторными уравнениями, то есть рассмотрим его для случая двух статистических величин и . Далее, рассмотрим его на примере линейного уравнения вида

,

или для элементов этих величин

.

Тогда исходное условие МНК выглядит так:

.

Действительно, если выборки случайных величин и заданы, то уравнение регрессии становится функцией только лишь неизвестных коэффициентов .

Функция представляет собой квадрат расстояния между действительными значениями случайной величины и соответствующими им значениями будущего уравнения регрессии. Это расстояние возведено в квадрат, чтобы уйти от знака этой разности. Главным требованием, согласно записанному выражению, является сведение этого расстояния к минимуму. Если это требование будет достигнуто, то полученные коэффициенты будут адекватно отображать функциональную зависимость между величинами и .

Далее, согласно методам математическому анализа, условие минимума может быть достигнуто, если все частные производные по неизвестным коэффициентам, будут равны 0

Найдем частные производные по правилам математического анализа:

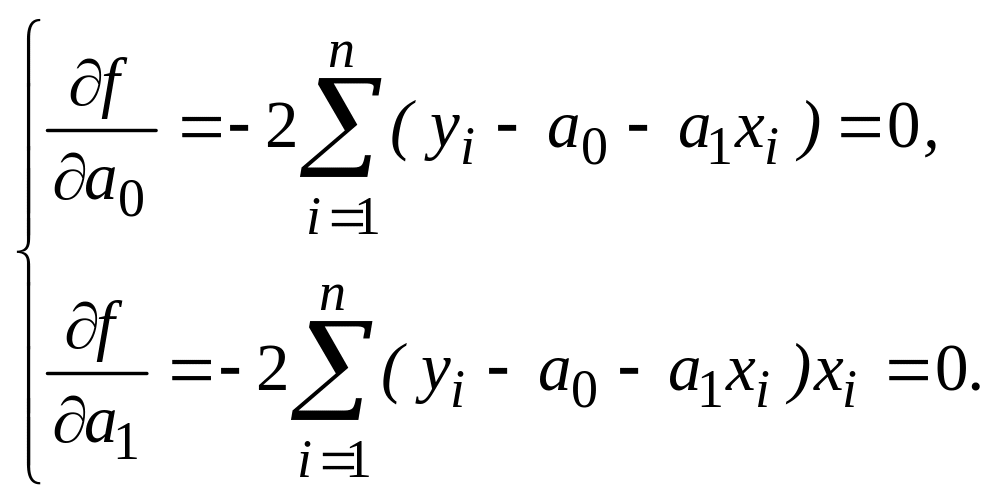
Так как , то

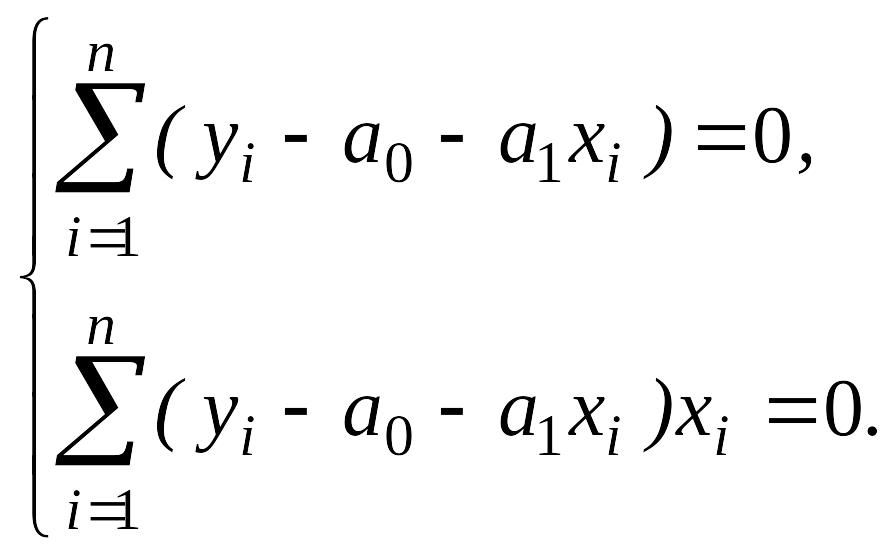
Раскроем сумму

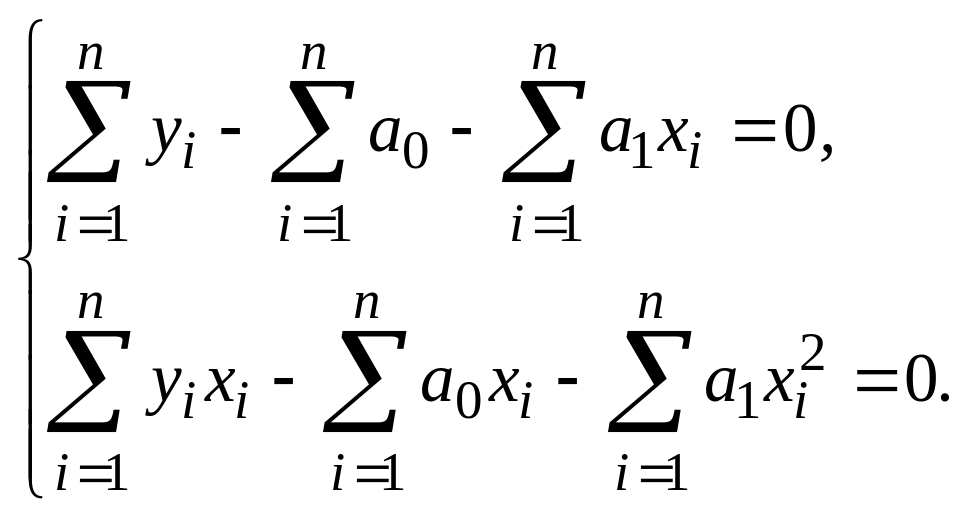
Учтем, что

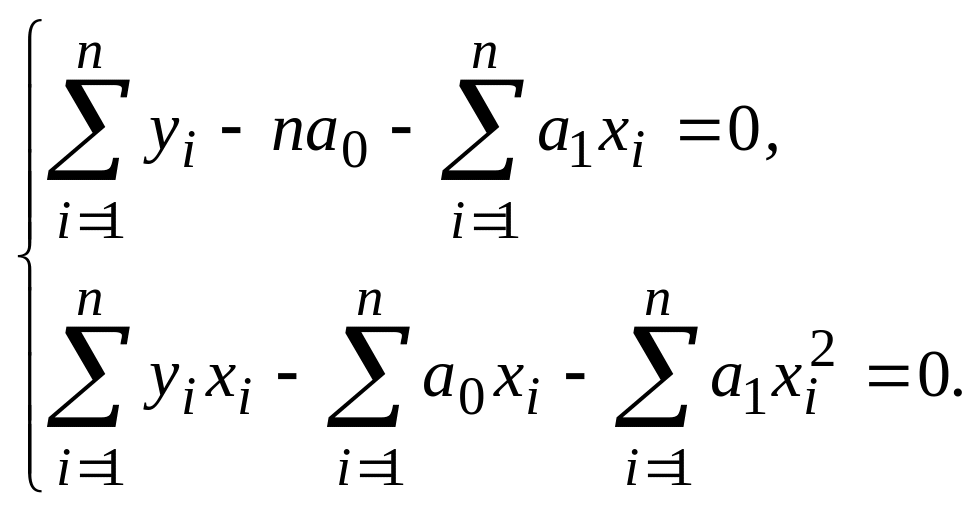
Перенесем неизвестные в левую часть, а известные – в правую.

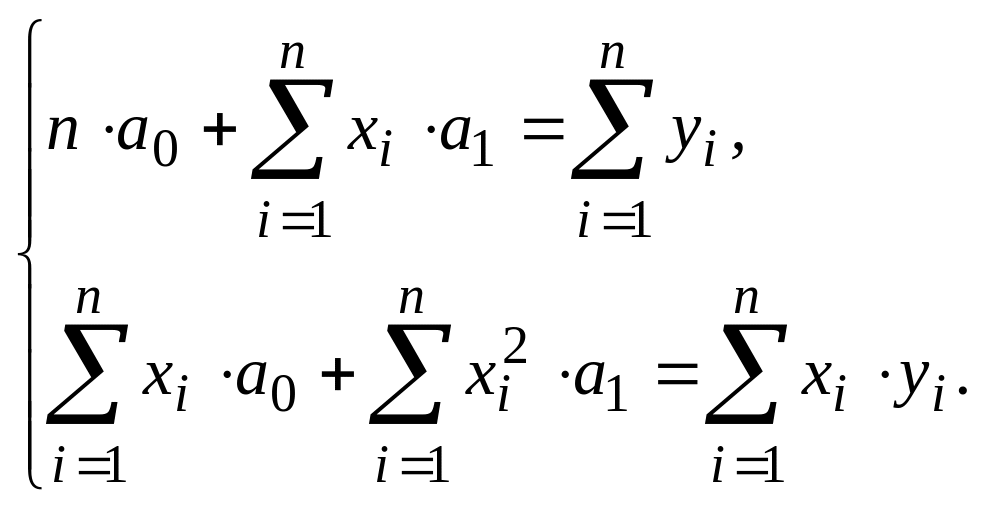
Это СЛАУ, она может быть решена методом Крамера:

,

.

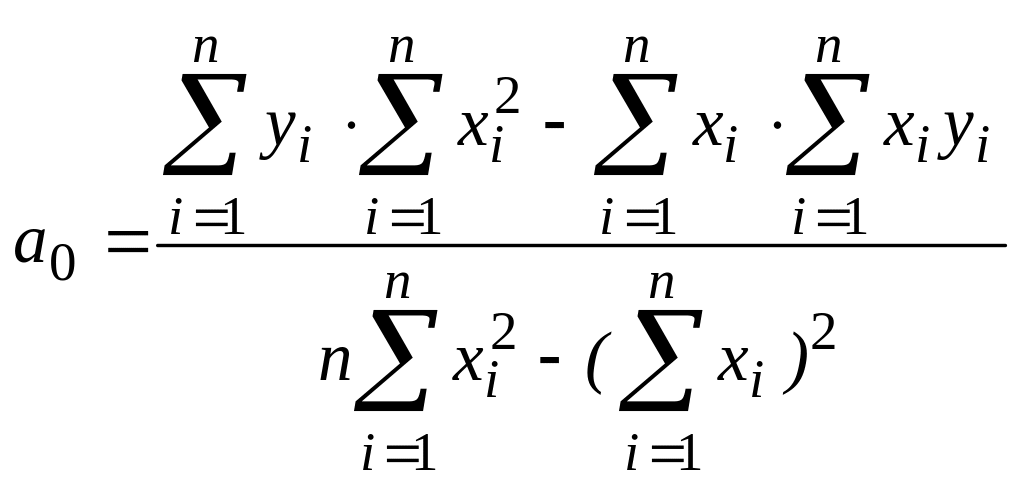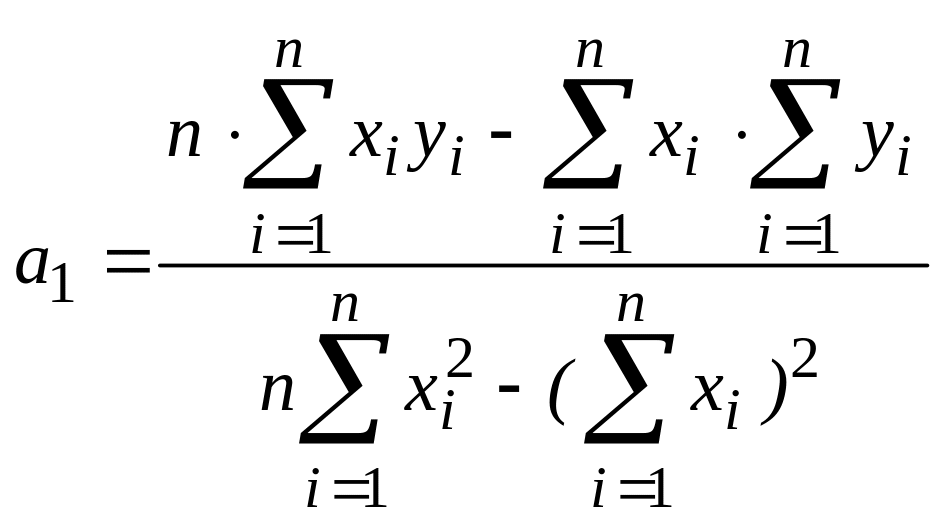Как видно, в проведенных рассуждениях нигде не нарушалась общность, значит, их можно провести и для более сложного уравнения регрессии.

Применим МНК для расчета линейного многофакторного уравнения регрессии. Возьмем простейший случай 2-х переменных

.

Проводя рассуждения аналогичны рассмотренным выше, получим

.

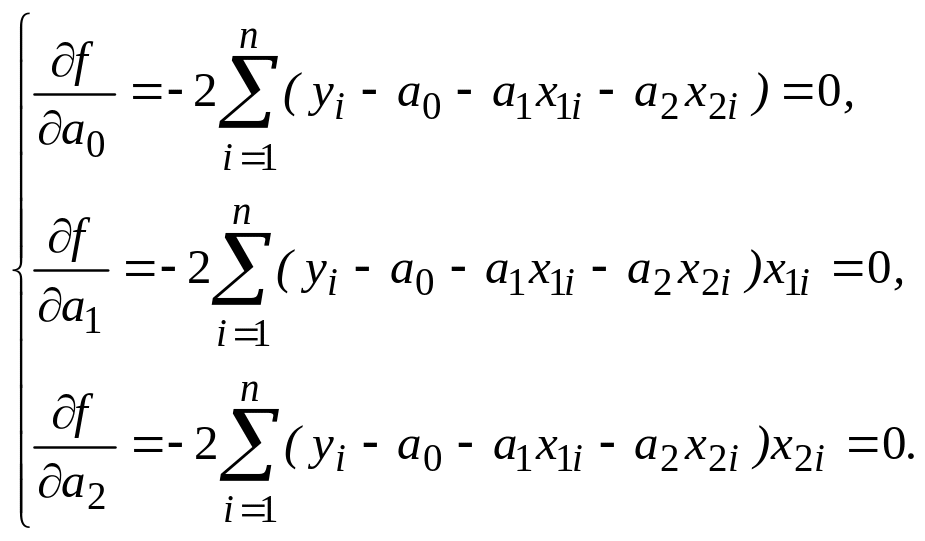
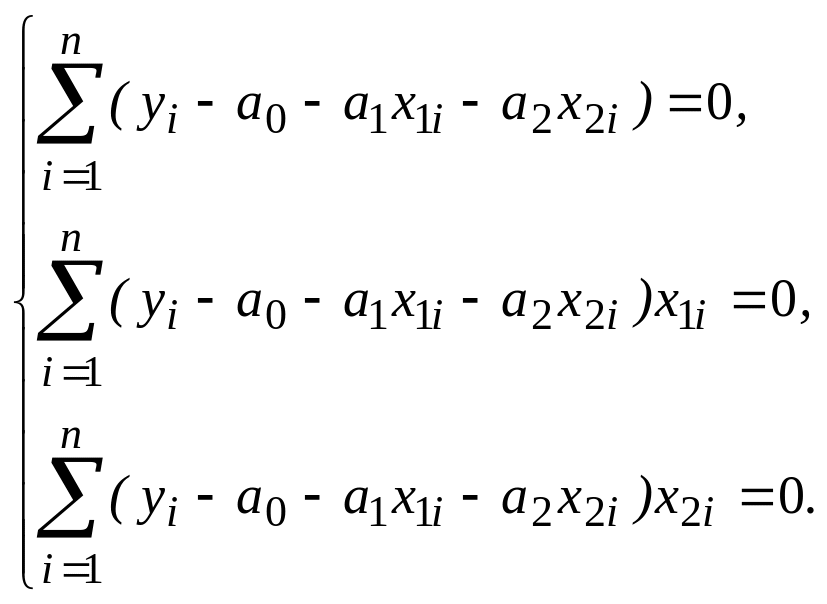
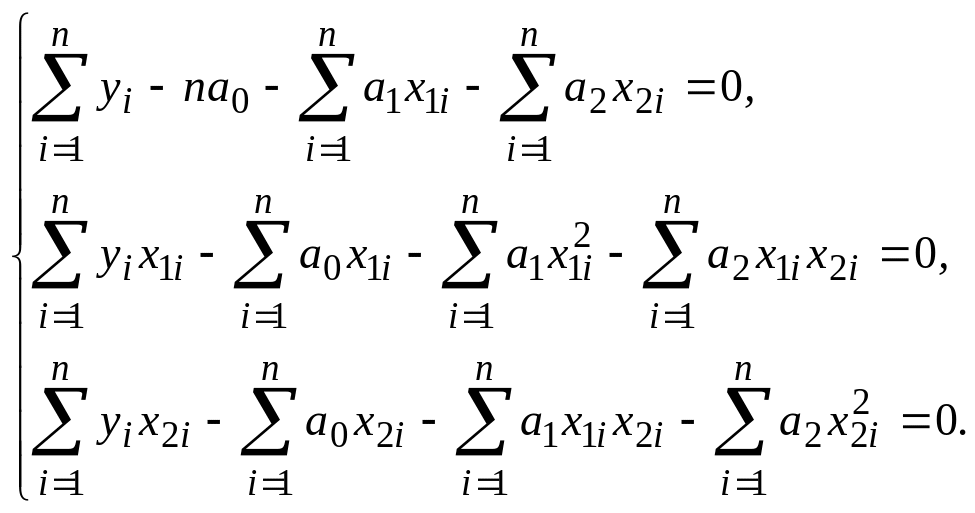
Получим СЛАУ

.

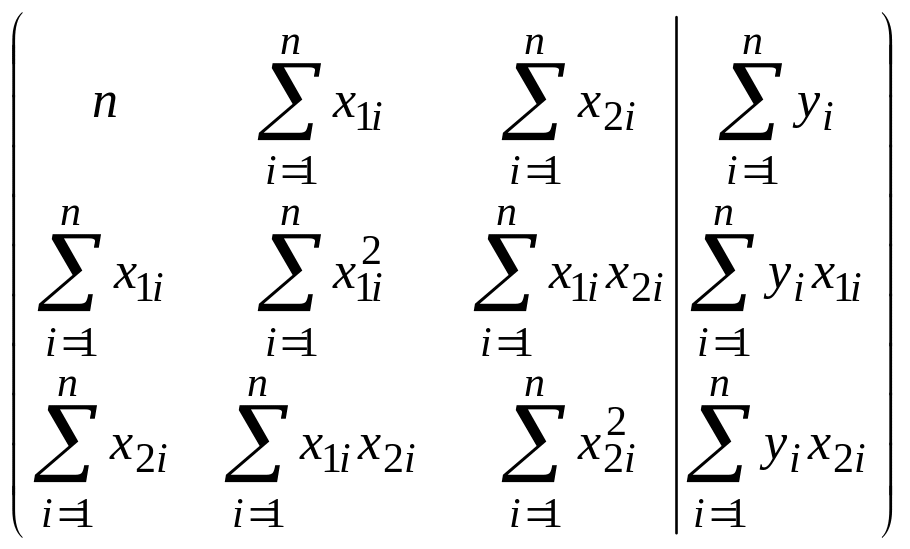Пример 1.

Составить линейное однофакторное уравнение регрессии для статистических величин и , приведенных в таблице 1.1

Таблица 1.1
	1	2	3	4	5	6	7	8	9	10
xi	3,6	4,3	4,3	6,8	7,5	7,3	9	9,9	11,7	16,5
yi	133	124	121	119	113	101	97	94	92	92

Решение.

Произведем расчет всех коэффициентов СЛАУ:

;

;

.

Мы получили СЛАУ

.

Решим методом Крамера

;

;

.

Найдем искомые коэффициенты

.

Значит, искомое уравнение имеет вид:

.

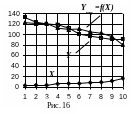
На рис. 16 показаны выборки и , а также линейная зависимость , дающая неплохое совпадение с выборкой .

Пример 2.

Составить линейное многофакторное уравнение регрессии для статистических величин , и , приведенных в таблице 2.1

Таблица 2.1
	1	2	3	4	5	6	7	8	9	10
x1i	2	6	8	10	12	10	8	6	7	8
x2i	15	18	17	15	18	22	18	14	16	20
yi	65	98	123	139	163	150	123	100	114	118