VI. Проверка статистических гипотез

1. Понятие статистической гипотезы

Статистической гипотезой называют некоторое предположение о свойстве генеральной совокупности, которое может быть проверено по данным выборки. Гипотеза обозначается буквой .

Гипотезы о параметрах генеральной совокупности называются параметрическими, о распределениях – непараметрическими.

Гипотеза о том, что две совокупности неразличимы по одному или нескольким признакам, называется нулевой. Например, - гипотеза о равенстве средних значений двух совокупностей.

Нулевая гипотеза отвергается, когда по выборке (выборкам) получается результат, маловероятный при истинности этой гипотезы.

Границей невозможного (или маловероятного) считают величину уровень значимости (обычно . Чем больше величина , тем легче принять гипотезу.

Статистическим критерием называют характерную для каждой гипотезы переменную, величина которой при соответствующих условиях по заданному правилу указывает, следует принять или отвергнуть проверяемую нулевую гипотезу.

Процедура проверки статистической гипотезы содержит следующие этапы.

1. Формулируется задача в виде статистической гипотезы.

2. Выбирается статистический критерий для ее проверки.

3. Формируются статистические данные для расчета критерия.

4. Вычисляется опытное значение критерия.

5. Принимается решение о принятии выдвинутой гипотезы.

При проверке гипотезы возможны два ошибочных решения:

1. гипотеза верна, но она отвергается: ошибка 1-го рода;

2. гипотеза не верна, но она принимается: ошибка 2-го рода.

Обе эти ошибки возможны, если для проверки критерия были взяты нерепрезентативные выборки.

2. Гипотеза о законе распределения

При проверке этой гипотезы устанавливается соответствие между экспериментальным и каким-либо теоретическим распределением. Если такое удается сделать, то анализ данной выборки существенно упрощается, поскольку для всех известных теоретических распределений существуют справочные данные, которыми можно будет легко воспользоваться.

В качестве критерия согласованности применяется критерий Пирсона или

,

где - число интервалов, и - частоты j-го интервала опытного и теоретического распределения соответственно. Значения задаются исходной статистической таблицей, а - таблицей того теоретического распределения, которое нуждается в проверке. Иногда в формуле вместо абсолютных частот, используют относительные и .

Проверяемая гипотеза не отвергается, если .

Значения берутся из специальной таблицы (Приложение 2), и они зависят от уровня значимости (будем брать и числа степеней свободы f– количества независимых переменных, определяющих данное распределение.

Для нормального распределения , где = 3 – число условий, налагаемых на частоты.

После проверки гипотезы принято строить оба распределения на одной системе координат, в одном масштабе.

Пример 1.

Таблица 1.1.
№	1	2	3	4	5	6	7	8	9	10
nj on	2	4	9	15	19	19	15	9	4	2
nj теор	3	6	9	16	21	16	12	8	3	3

По данным таблицы 1.1. проверить гипотезу о соответствии статистических данных нормальному закону распределения вероятностей. Построить полигоны обоих распределений.

Найдем значение , результаты вычислений занесем в таблицу 1.2.

Таблица 1.2.
№	1	2	3	4	5	6	7	8	9	10
nj on	2	4	9	15	19	19	15	9	4	2
nj теор	3	6	9	16	21	16	12	8	3	3
∆ nj	-1	-2	0	-1	-2	3	3	1	1	-1
(∆ nj)2	1	4	0	1	2	9	9	1	1	1
(∆ nj)2/ nj теор	0,5	1	0	0,067	0,21	0,47	0,6	0,11	0,25	0,5

Для каждого j найдем величину ∆ n_j = n_{j on} - n_{j теор}:

;

; и

………………;

.

Для каждого j найдем величину (∆ n_j)²:

;

;

………………;

.

Просуммировав значения последней строки, определим

.

В приложении 2 находим величину , задавшись значениями и

.

Поскольку , гипотеза не отвергается.

Построим полигоны обоих распределений (рис. 12).

3. Гипотеза о равенстве средних значений

При проверке статистической гипотезы о равенстве средних значений формулируется гипотеза . В качестве критерия используется критерий Стьюдента, рассчитываемый по формуле:

,

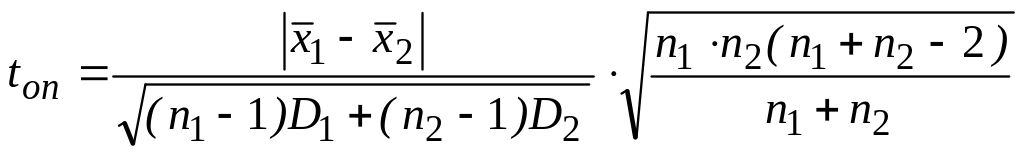где и - средние значения для первой и второй выборки соответственно; и - дисперсии этих выборок; и - объемы этих выборок.

При отыскании величины задаются критерием значимости , и числом степеней свободы .

Проверяемая гипотеза не отвергается, если .

Пример 1.

Таблица 1.1.
№	1	2	3	4	5	6	7	8	9	10
x1j	40	31	27	64	25	38	22	75	63	80
x2j	16	38	63	45	78	64	43	43	55	50

По двум выборкам ДСВ , приведенным в таблице 1.1, проверить статистическую гипотезу о равенстве средних значений.

Решение.

Найдем величины и по известным формулам:

; (см. пример 2, пV.3).

; .

Найдем величины и по формулам:

; .

Результаты вычислений сведем в таблицу 1.2.

Таблица 1.2.
№	1	2	3	4	5	6	7	8	9	10
n1j	40	31	27	64	25	38	22	75	63	80
n2j	16	38	63	45	78	64	43	43	55	50
x1j-	-6,5	-15,5	-19,5	17,5	-21,5	-8,5	-24,5	28,5	16,5	33,5
x2j-	-33,5	-11,5	13,5	-4,5	28,5	14,5	-6,5	-6,5	5,5	0,5
(x1j- )2	42,3	240,3	380,3	306,3	462,3	72,3	600,3	812,3	272,3	1122
(x2j- )2	1122	132,3	182,3	20,3	812,3	210,3	42,3	42,3	30,3	0,3