Геометрическое программирование
Под задачами геометрического программирования понимают задачи наиболее плотного расположения некоторых объектов в заданной двумерной или трехмерной области. Такие задачи встречаются в задачах раскроя материала для производства каких-то изделий и т.п. Это - еще недостаточно разработанная область математического программирования и имеющиеся здесь алгоритмы в основном ориентированы на сокращение перебора вариантов с поиском локальных минимумов.
Дискретное программирование
Многие задачи исследования операций такие как распределение ресурсов, сетевого планирования, календарного планирования описываются математическими моделями дискретного программирования.:
Найти
при
условиях:
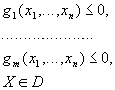
-множество
. Если множество
является
конечным или счетным, то условие
—
условие дискретности и данная задача
является задачей дискретного
программирования.
Чаще
всего условие дискретности разделено
по
отдельным переменным следующим образом:
,
где
конечное
или счетное множество.
Если
вводим ограничения
—
целые числа, то приходим к задачам
целочисленного программирования,
которые являются частным случаем
дискретного программирования. В задачах
дискретного программирования область
допустимых решений является невыпуклой
и несвязной, поэтому отыскание решения
в таких задачах сопряжено со значительными
трудностями. В частности невозможно
применение стандартных приемов,
используемых при замене дискретной
задачи ее непрерывным аналогом, состоящих
в дальнейшем округлении найденного
решения до ближайшего целочисленного.
Дискретное программирование - это раздел математического программирования, в котором изучаются методы решения оптимизационных задач с несвязной областью допустимых решений: в общем случае эта область распадается на ряд отдельных не связанных друг о другом подмножеств, а в частном случае - состоит из отдельных точек.
Многочисленные проблемы, возникающие при решении задач дискретного программирования, определили то обстоятельство, что наибольшее число разработанных эффективных методов решения ориентировано на задачи с линейными целевыми функциями и ограничениями.
Основная
производственная задача для дискретного
производства.
Необходимо выбрать план производства
дискретной продукции таким образом,
чтобы при ограничениях на используемые
сырьевые ресурсы обеспечить наибольшую
прибыль от ее реализации. Формальная
запись задачи в матричной форме имеет
вид
где
х - n-мерный вектор-столбец целочисленных
оптимизационных переменных, определяющий
количество производства n видов дискретной
продукции; С - n-мерный вектор-cтрока
коэффициентов целевой функции,
определяющий прибыль от реализации
единицы продукции каждого вида;
-
n-мерное множество целых неотрицательных
чисел; А - (m x n)-мерная матрица, определяющая
затраты сырьевых ресурсов на производство
единицы продукции каждого вида; b -
n-мерный вектор-столбец, определяющий
наличное количество сырьевых ресурсов
(m - количество видов ресурсов).
Задача
о ранце.
Турист готовится к длительному переходу.
Он может нести груз весом b , который
может включать n типов предметов. Каждый
отдельный предмет типа j весит a[j] (j
=1,n), а полезность его использования в
переходе оценивается числом c[j]. Необходимо
определить, сколько предметов каждого
типа турист должен положить в рюкзак,
чтобы суммарная ценность снаряжения
была максимальной. Формальная запись
задачи имеет следующий вид:
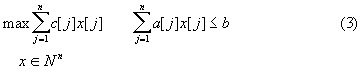К
такого рода задаче в первом приближении
может быть сведена задача комплектации
оборудованием многоцелевого летательного
аппарата.