Целочисленное линейное программирование

В целом ряде решаемых задач линейного программирования на переменные накладывается дополнительное условие их целочисленности. Действительно, ведь нельзя изготовить, скажем, 1/2 стола или сшить 1/3 костюма. Когда наложено дополнительное условие целочисленности переменных , соответствующая задача носит название задачи целочисленного линейного программирования.

Простое округление до целых чисел здесь не помогает - план может получиться не оптимальным. Поэтому приходится разрабатывать специальные алгоритмы решения таких задач, к наиболее известным из которых относятся так называемые алгоритмы Гомори, основанные на так называемой идее отсечения.

        Задача тематического планирования. Предприятие имеет на плановый период портфель заказов, включающий р разработок. Каждая j -я разработка характеризуется количественной оценкой эффекта e[j], получаемого от ее выполнения, и объемом работ d[ij] который должен быть выполнен i -м подразделением предприятия (i =1,m). Общий объем работ, который может быть выполнен каждым подразделением, - b[i]. Существует возможность передачи работ из одних подразделений в другие, родственные им по специализации. Эта возможность отражается параметрами a[ij] ( a[ij] = 1, если i-е подразделение может выполнять работы j -то подразделения, и a[ij] = 0 - в противном случае). Введем в рассмотрение оптимизационные переменные если j-я разработка включается в план предприятия, w[j] = 0 - в противном случае) и - объем работ i -го подразделения предприятия, выполняемый j -м подразделением. Необходимо так составить тематический план предприятия, чтобы при ограничениях на объемы работ, проводимых каждым подразделением с учётом их взаимозаменяемости, обеспечить максимальный эффект от выполнения разработок. Формализованная запись задачи будет иметь следующий вид:         (8)

Булевское программирование

К частному случаю задачи целочисленного линейного программирования относятся задачи, где переменные могут принимать всего лишь два значения - 0 и 1. Соответствующие задачи часто называют задачами булевского программирования. Наиболее известные из этих задач - это задача о назначениях (какого работника на какую работу поставить), задача выбора маршрута (задача коммивояжера, задача почтальона), задача о максимальном паросочетании и т.д.

Для решения задач этого типа разрабатываются очень специфические алгоритмы, основанные на комбинаторике, графах и т.д.

        Задача о назначениях. Существует целый ряд разновидностей постановок задач о назначениях (ЗН). Рассмотрим наиболее простую из них. Имеется n машин и n работ. Каждая машина может быть назначена на выполнение одной из n работ. Для выполнения каждой работы необходима лишь одна из имеющихся - n машин. Выполнение j-й работы i-й машиной характеризуется затратами С[i,j]. Необходимо определить такую перестановку n машин по n работам, чтобы суммарные затраты были минимальными. К такого рода задаче, например, может быть сведена задача целераспределения активных средств противовоздушной обороны по нелетающим объектам. Формальная запись задачи имеет следующий вид: 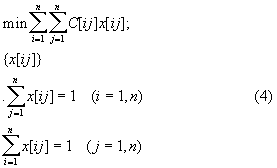где x[ij] - оптимизационная переменная, принимающая значения: 1, если i -я машина назначена на выполнение j -и работы, и 0 - в противном случае; ограничения первого типа определяют, что каждая i -я машина может выполнять лишь одну работу; ограничения второго типа определяют, что для выполнения j -и работы необходима лишь одна машина.         Таким образом, ограничения обоих типов соответствуют условиям реализации перестановки n машин по n работам.         Задача коммивояжера. Имеется n городов. Задана матрица расстояний между городами (в общем случае необязательно симметричная), каждый элемент которой c[ij] определяет расстояние, между i -м и j -м городом ( ). Коммивояжеру необходимо составить план обхода всех городов, осуществляя заход в каждый город лишь один раз таким образом, чтобы минимизировать общий пройденный путь. К такого рода задаче может быть сведена задача инспектирования нескольких космических объектов за один полет космического корабля многоразового использования. Формальная запись задачи имеет следующей вид: