МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЧОРНОМОРСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ

імені Петра Могили

ПРОЕКТУВАННЯ ТА АНАЛІЗ

АКТИВНОГО ЕЛЕКТРИЧНОГО ФІЛЬТРА

Методичні вказівки до виконання

розрахунково-графічного завдання

з дисципліни «Методи і засоби реєстрації та відновлення інформації»

для студентів спеціальності

6.090900 "Медичні прилади і системи"

Миколаїв - 2009

ВСТУП

Передача і обробка цифрових сигналів електрозв'язку, сигналів радіо і телебачення і так далі вимагають створення електронних ланцюгів, які в певній смузі частот володіли б наперед заданими властивостями амплітудно-частотних і фазо-частотних характеристик (АЧХ і ФЧХ). Методи проектування і аналізу таких пристроїв відносяться до традиційних методів теорії ланцюгів.

Розрахунково-графічне завдання присвячене поглибленому вивченню цих методів на прикладі проектування активного електричного фільтру.

Електричним фільтром називається електричний ланцюг, призначений для виділення коливань в певному діапазоні частот. Діапазон частот, що пропускається фільтром називається смугою прозорості (пропускання) або СП. Область частот, в якій всі частоти пригнічуються із заданим ослабінням, називається смугою затримання або СЗ.

Відповідно до діапазону частот, що пропускаються фільтром, вони діляться на наступні типи (fзр - частота зрізу АЧХ):

ФНЧ - фільтри нижніх частот - ПП від 0 до fзр;

ФВЧ - фільтри верхніх частот - ПП від fзр до Г;

СФ - смугові фільтри - СП від fзр1 до fзр2;

ЗФ - фільтр, що загороджує, - СЗ від fзр1 до fзр2;

ФФ - фазові фільтри - СП від 0 до Г і заданої корекції фази.

Залежно від вхідних в них компонентів фільтри підрозділяють на:

реактивні або LC-фільтри;

резистивно-ємкісні або RC-фільтри;

активні або ARC-фільтри.

У роботі студент повинен спроектувати ARC-фільтр на основі ідеального операційного підсилювача (ОП). Тип фільтру визначається розташуванням нулів і полюсів, по ним же обчислюються параметри елементів.

Проектована схема і вигляд вхідного сигналу задаються відповідно до номеру варіанту. Теоретичні передумови і методи синтезу і аналізу вибіркових ланцюгів на основі ОП наводяться в [1, 2, 3, 4].

1. Проектування arc-фільтра

Розглянемо загальні принципи реалізації передавальної функції другого порядку

(1)

за допомогою ОП, охопленого зворотним зв'язком (ЗЗ). Пасивна частина схеми є багатополюсником, що складається з резистивних і ємкісних елементів (рис.1)

Р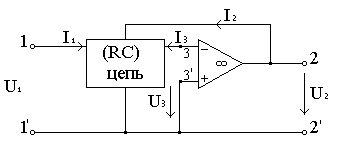 ис.1 Электронна схема на основі ОП з ЗЗ

Складемо рівняння пасивного триполюсника у Y-формі.

(2)

За умови ідеального ОП його вхідний ланцюг (затиски 3-3’) не споживає струму, тобто I₃ = 0. Враховуючи, що U₂ = - K₀U₃, з третього рівняння системи (2) отримаємо

. (3)

При K   передавальна функція ланцюга визначається лише параметрами RC-кола:

. (4)

Передбачимо, що RC-багатополюсник має структуру, що показана на рис.2 б і складається з п'яти пасивних компонентів (R- і C-елементів)

Скористаємося властивостями ідеального ОУ: різниця потенціалів між його вхідними затисками дорівнює нулю, тобто U₃ = 0 (см.рис.2). Це означає, що потенціал затиску 3 дорівнює нулю. Складемо рівняння вузлів 4 і 3:

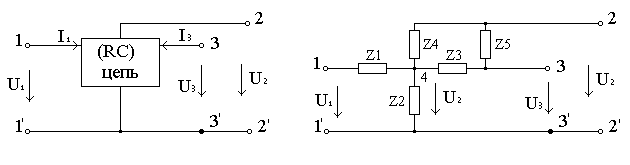а) б)

Рис.2. Пасивний триполюсник (а) і його 5-елементна конфігурація (б)

Вирішуючи друге рівняння цієї системи відносно вихідної напруги U₂, тобто , і, підставляючи результат в перше рівняння, після не складних перетворень отримаємо вираження для коефіцієнта передачі по напрузі:

(5)

де

Задаючи як провідність Y_i провідність ємності pC_i або провідність опору 1/R_i, можна скласти необхідний вигляд передавальної функції K_U(p).

1. НЧ-фільтр другого порядку. Його передавальна функція має вигляд:

(6)

Аби права частина рівняння (5) відповідала дробу (6), слід вибрати як ємкості елементи Y2 і Y5, останні представити опорами. Тоді передавальна функція може бути виражена через параметри елементів (RC) -схеми (рис.3):

(7)

Таким чином, із зіставлення функцій (6) і (7) виводиться система з трьох рівнянь для визначення параметрів елементів пасивного триполюсника:

(8)

Оскільки невідомих параметрів п'ять, то два з них можуть задаватися довільно. Зазвичай вибирається якась ємкість, наприклад C₂ = C₀ з нормального ряду параметрів і постійна часу ₀ = R₁C₂, т.е. R₁ = ₀ / C₀. Параметри останніх елементів знаходяться підстановкою C₂ та R₁ у систему (8) з подальшим її рішенням:

(9)

Рис. 3. Активний НЧ-фільтр другого порядку

1.2. СФ другого порядку. Передавальна функція смугового фільтру

(10)

Також може бути реалізована за допомогою пасивного трехполюсника в конфігурації, зрисованої на рис.2,б. Якщо вибрати провідність Y_1­ и Y₅ ємнісними, тобто Y₁ = pC₁, Y₅ = pC₅, а останні елементи резистивними, то передавальна функція може бути представлена через параметри елементів (рис.4):

(11)

Як і в попередньому пункті, задаючись C₁ = C₀,  = С₁ /С₅, С₅ = С₁ / , вирішуємо систему трьох рівнянь для визначення параметрів інших елементів:

(12)

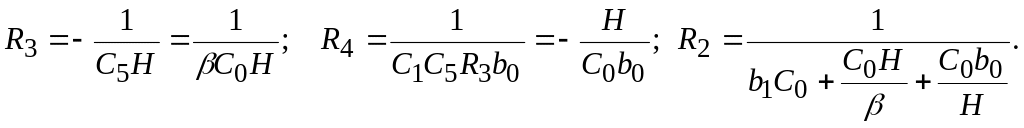(13)

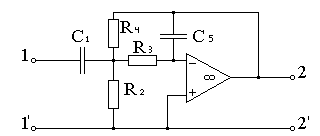
Рис. 4. Активний СФ другого порядку

1.3. ВЧ-фільтр другого порядку має передавальну функцію

(14)

яка так само може бути реалізована на ОП з триполюсником у вигляді однорідних R і C-елементів. Чисельник дробу (14), рівний результату множення Y₁Y₃, задає ємнісний характер елементів Y₁ = pC₁ и Y₃ = pC₃. Для здобуття в знаменнику дробу доданку з другою мірою від p (див. вираз (5)) необхідно задати ще один ємнісний елемент, а саме Y₄ = pC₄. Останні елементи мають бути резистивними (рис.5.): Y₂ = 1/R₂ , Y₅ = 1/R₅ .

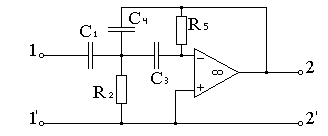
Рис. 5. Активний ФВЧ другого порядку

Коефіцієнт передачі по напрузі, виражений через параметри елементів, має вигляд:

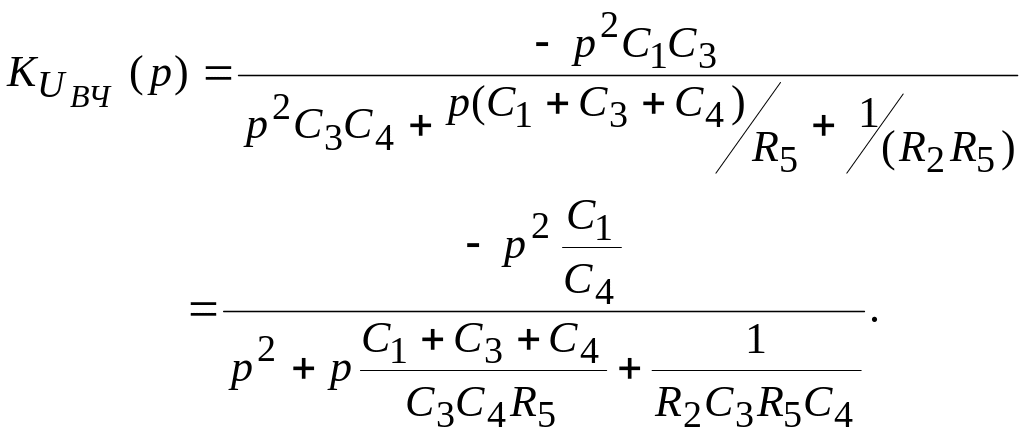(15)

Зіставивши вирази (14) і (15), можна отримати систему, за допомогою якої визначаються параметри елементів схеми ФВЧ:

(16)

Задаючись додатковими умовами С₁ = С₀ и  = C₄R₅ до системи (16) отримаємо наступний обчислювальний алгоритм:

(17)