Теорема отсчетов (Теорема отсчётов Уиттакера — Найквиста — Котельникова — Шеннона)

Представим себе, что нам нужно оцифровать аналоговый сигнал, амплитуда которого задана непрерывной функцией времени u(t) (рис.1а).

Категория непрерывности в математике имеет определенный смысл ( , и т.д.) - но и представления на уровне здравого смысла будет достаточно. Как мы помним, "упрощение реальности" идет и по оси t (выборка есть счетное множество), и по оси u (ограничения, накладываемые разрядностью чисел, используемых для записи результатов) (рис.1б). Переход от непрерывного сигнала к множеству выборок его значений в определенные моменты времени (t0, t1, t2 ,...) называется дискретизацией (или семплированием), а представление амплитуды в соответствии с заданной разрядностью - квантованием. Дискретизацию можно сравнить с киносъемкой, где непрерывное движение фиксируется конечным числом кадров в единицу времени.

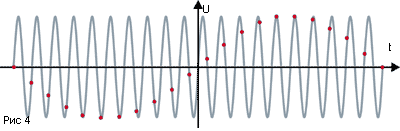
Забудем на время о квантовании (будем считать, что выборки соответствуют точным значениям u(tn)) и попробуем решить, насколько часто нужно делать выборки, то есть, какова должна быть частота дискретизации, если мы хотим впоследствии по отсчетам восстановить исходный сигнал. На рисунках 3 и 4 показаны попытки дискретизации синусоидального сигнала, красные точки соответствуют дискретным значениям - отсчетам (семплам).

Частота исходного сигнала на рис. 3 составляет 0,09 от частоты дискретизации. Результат можно считать приемлемым, так как, соединив соседние точки, получим кривую, близкую к форме исходного сигнала. А вот про случай на рис.4 этого не скажешь. Здесь частота сигнала близка к частоте дискретизации (0,95), и в результате отсчеты выстраиваются в синусоиду, только совсем другую, с частотой раз в двадцать меньше. Нечто подобное можно иногда наблюдать в кино, когда колеса у кареты вдруг начинают крутиться в обратную сторону.

Феномен изменения частоты синусоиды в результате дискретизации называется aliasing (alias по-английски - псевдоним). О восстановлении исходного сигнала говорить уже не приходится.

Интуитивно понятно, что чем чаще делаются выборки, тем точнее мы отобразим характер изменения функции, однако увеличивать частоту дискретизации до бесконечности мы не можем, и нам нужен критерий, где остановиться. Критерий определяется знаменитой теоремы отсчетов, имеющей и другие названия: теорема Котельникова, теорема Найквиста (Nyquist), теорема Шеннона (Shannon).

Теорема отсчётов Уиттакера — Найквиста — Котельникова — Шеннона гласит, что, если аналоговый сигнал x(t) имеет спектр, ограниченный частотой F_max, то он может быть однозначно и без потерь восстановлен по своим дискретным отсчётам, взятым с частотой:

f_дискр

где F_max — верхняя частота в спектре, или, по-другому, по отсчётам, взятым с периодом:

T_дискр

Крайне важен принцип восстановления исходного сигнала. Ведь через набор точек на плоскости, соответствующих отсчетам, можно провести бесчисленное множество кривых! (рис.5) Или имеется в виду “лестница" (рис. 9)? Теорема отсчетов говорит о том, что непрерывный сигнал можно представить в виде следующего ряда:

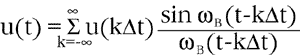
Здесь k - номер отсчета; произведение k t - момент времени, соответствующий k-му отсчету; u(k t) - само значение k отсчета, и ω_В максимальная (верхняя) частота спектра, выраженная в радианах. Часто величину t называют шагом (интервалом) дискретизации, а ω_В - частотой Найквиста.

Под интегральной суммой написана формула отсчётов фунцкии x(t). Мгновенные значения этой функции есть значения дискретизированного сигнала в каждый из моментов времени.

Так же имеет место и следующее утверждение: Если максимальная частота в сигнале превышает половину частоты прерывания, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.

Теорема отсчетов Котельникова дуальна теореме Найквиста: в первой идет речь о передаче непрерывного сигнала с помощью его отчетов (по каналу с дискретным временем), а во второй – о передаче дискретного сигнала (последовательности отсчетов) по непрерывному каналу. В первой теореме , а во второй - . В первом выражении W – полоса сигнала, во втором – полоса канала. На практике равенство не достижимо.

Замечание. Из определения спектра сигнала следует, что конечный по длительности сигнал имеет бесконечно широкий спектр. Поэтому при дискретизации конечного по длительности сигнала (например, песни на аудиодиск) невозможно восстановление из отсчетов без потери качества.

Таким образом, достаточно располагать частой выборкой значений u(k t), и исходная функция (сигнал) восстанавливается полностью, ибо равенство в формуле не приближенное, а строгое. Однако если быть абсолютно точными, равенство справедливо в случае, если мы, скажем, оцифровываем музыкальное произведение, длящееся сбесконечно, и которое никогда не кончится. Если же рассматривать ограниченный отрезок времени, то бесконечной сумма может стать, если t будет бесконечно малой величиной ( t 0). Раз уж мы подступаемся к бесконечности (непрерывности) с ограниченными выборками, придется забыть о строгих равенствах.

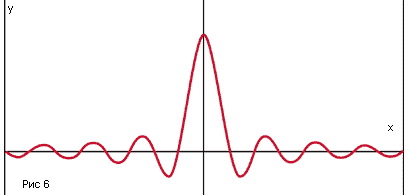
И, тем не менее, переходя к практике, можно убедиться, что и теорема, и формула действительно работают. Попробуем разобраться, как это происходит. Во-первых, выражение на которое умножается значение отсчета в формуле (1), является функцией вида sin x/x, сжатой вдоль горизонтальной оси в B раз (рис. 6).

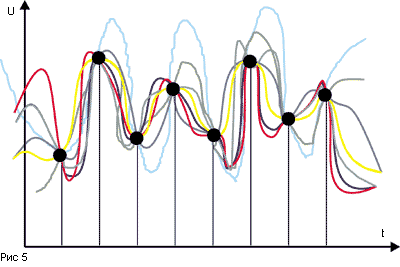
Это так называемая функция Котельникова (базисная функция, функция отсчетов). То, что x здесь равно не B*t, а B*(t- k t), приводит к тому, что график сдвигается влево на k t. В итоге получается "частокол" из функций с вершинами в точках, соответствующих значению отсчетов u(k t), так как максимум любого сомножителя (2) есть единица. Этот частокол и надо просуммировать. Вот результаты небольшой лабораторной работы на эту тему (рис.7).

В качестве шага дискретизации было выбрано число 1 (следовательно, B = ), и всего три отсчета: u(0) = 1,2 (коричневая кривая на рисунке), u(1) = 1,4 (зеленая) и u(2) = 1,6 (синяя). Таким образом, слагаемых было не бесконечное число, а всего три, и, тем не менее, результат получился довольно убедительный: суммирующая кривая красного цвета проходит через все три точки, плавно соединяя их, и быстро сходит на нет справа и слева (рис.7 и 8).

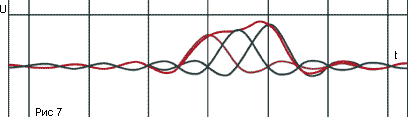
Общее же свойство таково: при любом произвольном количестве слагаемых результирующая кривая точно проходит через выбранные точки отсчетов, а в промежутках между ними сколь угодно близко приближется к исходному сигналу (по мере роста числа слагаемых). Все вышесказанное не означает, разумеется, что цифро-аналоговые преобразователи обязательно восстанавливают исходный сигнал по значениям отсчетов именно таким образом. Но важно то, что "правильное" восстановление в принципе существует.

Квантование

Следующим ключевым моментом является цифровое представление значений отсчетов ("прореживание" вертикальной оси u) - квантование. Реальные значения должны быть представлены в виде N-разрядного двоичного числа. Такое число может принимать 2N различных значений. Например, для 16-битных чисел N=16, а 2N = 65536. Вот на столько долей надо разбить вертикальную ось, а после решать, в какой отрезок попадает то или иное значение отсчета. Совершенно очевидно, что чем больше разрядов в числе, тем более точной и полной будет кодируемая информация.

Мы сравнивали дискретизацию сигнала с киносъемкой, когда непрерывное движение представляется в виде череды кадров, и частота дискретизации аналогична частоте смены кадров. Если продолжить эту аналогию, то разрядность числа при квантовании можно соотнести с размером кадра. Ширина киноленты может варьироваться от 8 до 70 мм. Ясно, что кадр большего размера способен нести больше информации. Проблему измерений и представления результатов мы уже затрагивали в начале статьи. Можно для иллюстрации привести еще такой пример. Представим, что нам нужно измерить высоту дерева, а мы располагаем лишь шестом с метровыми отметками. Тогда придется считать, что высота дерева равна, скажем, 3 или 4 метрам, а то, что в действительности его длина составляет 3м 75 см, знать нам будет не дано.

Добавляя двоичному числу новый разряд, мы увеличиваем диапазон принимаемых им значений вдвое. Для амплитуды звукового сигнала, каковой и является наша функция u(t), это равносильно расширению динамического диапазона на 6 дБ. Таким образом, динамический диапазон цифрового звука прямо пропорционален разрядности числового (двоичного) представления отсчетов. Для 16-битных систем это будет величиной порядка 96 дБ, а для 24-битных - 144 дБ.

Рассмотренное здесь квантование относится к линейному типу, то есть весь диапазон изменения амплитуды сигнала делится на равные промежутки величиной 1/2N (шаг квантования на рис. 9).

Известны также примеры других, нелинейных моделей, когда разрядность переменна и зависит от амплитуды.

Проблемы и их решения

В силу вышесказанного оцифрованный сигнал будет иметь вид лесенки (рис. 9а). Математически это будет означать, что мы имеем дело с суммой двух сигналов - исходного и некоего дополнительного зигзагообразного (рис. 9б). Последний называется шумом квантования, и служит источником искажений.

Борьба с этим явлением происходит по принципу "лечить подобное подобным". Во входной сигнал подмешивается белый шум. Таким образом, нарушается неприятная для нас регулярность шума квантования. Этот феномен можно проиллюстрировать так. Если перед нами находится неподвижное велосипедное колесо, то объект, находящийся за ним, не удается рассмотреть как следует: мешают спицы. При быстром вращении спицы сливаются в серый, практически прозрачный круг. Сами спицы при этом никуда не деваются, но перестают быть помехой для наблюдателя.

Добавочный белый шум называется по-английски dither (дрожь). Сам процесс называется dithering. Из рисунка видно, что амплитуда шума квантования по абсолютной величине не превосходит . Величина = 1/2N соответствует младшему разряду N-битного числа, поэтому нужно обеспечить появление в этом разряде случайной величины, которая разрушит устойчивую форму шума квантования. Это и достигают, применяя dithering.

Dithering считается "неизбежным злом" в цифровой технике. Увеличивая общий уровень шума, он, тем не менее, обязательно присутствует практически в любом современном АЦП, независимо от того, заявлено это в документации или нет. (Там, где он отсутствует, это заметно по неудовлетворительному качеству звучания). Кроме АЦП, dithering зачастую применяется в других цифровых процессорах - эквалайзерах, компрессорах и пр.

Другой серьезной проблемой является aliasing, о котором уже упоминалось выше. Это явление возникает при попытке оцифровать сигнал, частота которого превышает частоту Найквиста. Специалисты из Apogee Electronics Corporation Хулио Альварес (Julio Alvarez) и Ричард Элин (Richard Elen), которые и предложили аналогию с киносъемкой, так объясняют этот феномен. Допустим, мы снимаем на ленту периодически вспыхивающую лампу, постепенно увеличивая частоту вспышек. В какой-то момент частота вспышек будет равна половине частоты смены кадров. В этот период на ленте будут чередоваться кадры со светом и темнотой, что нормально. Если же частота вспышек сравняется с частотой кадров, то на ленте везде будет свет, или везде - темнота, взависимости от того, в какую фазу мы попадем. Съемка, таким образом, становится бессмысленной.

Если мы выбираем частоту дискретизации равной, скажем, 44,1 кГц, то считаем, что она должна нам обеспечить предел слышимых частот, равный 20 кГц, а что дальше - не имеет значения. А вот и имеет! Если в сигнале, который мы, в соответствии с теоремой отсчетов, оцифровываем с частотой 2FB, обнаруживается составляющая, имеющая частоту FH > FB, то после оцифровки она будет иметь другую частоту: FHD = 2FB - FH, попадая в область слышимых частот (рис.10)

Ясно, что запись будет непоправимо испорчена. На графике амплитудно-частотной характеристики вертикальная линия, соответствующая FB , выполняет роль зеркала, отражая при оцифровке высокочастотные составляющие в левую по отношению к себе область графика. А такие высокочастотные паразитные составляющие в исходном сигнале обязательно будут присутствовать. Поэтому перед аналого-цифровым преобразованием сигнал необходимо пропустить через фильтр низких частот (ФНЧ). Но подробнее об этом поговорим ниже, а пока сформулируем еще одну проблему.

Полученный в результате аналого-цифрового преобразования дискретный сигнал является последовательностью прямоугольных импульсов. Из теории преобразований Фурье хорошо известно, что прямоугольный импульс (как, впрочем, импульс любой формы) может быть аппроксимирован, то есть представлен в виде суммы синусоидальных сигналов с соответствующими коэффициентами. Так что спектр простой периодической последовательности прямоугольных импульсов имеет довольно затейливый характер (рис. 11).

А если к тому же эта последовательность несет в двоичном виде информацию об исходном аналоговом сигнале u(t), который также имеет спектр определенного вида (рис.10б), то для нас не должно быть неожиданностью то, что окончательный спектр дискретного сигнала, как результата аналого-цифрового преобразования, представляет из себя столь пышный "букет" (рис 10в) периодической структуры. Проблема в том, что нужно выделить только центральный "лепесток", отбросив остальные. Как и в предыдущем случае, это можно сделать с помощью ФНЧ. Но здесь начинаются настоящие трудности. Фильтр и в том, и в другом случае должен иметь высокий порядок, не ниже 12-го. Создание таких фильтров вызывает значительные технические сложности, а, кроме того, фильтры высокого порядка вносят заметные фазовые искажения. Возможно, именно из-за неудач в этой области у многих надолго закрепилось отрицательное отношение к цифровому аудио.

Один из путей решения проблемы состоит в увеличении частоты дискретизации в несколько раз. Этот метод носит название oversampling или передискретизации. При аналого-цифровом преобразовании применяется аналоговая передискретизация, то есть выборка отсчетов делается на повышенной частоте. Другая разновидность - цифровая передискретизация, используется при цифро-аналоговом преобразовании. Это искусственное увеличение частоты дискретизации. Между соседними отсчетами вставляются несколько "фиктивных" нулевых отсчетов, и результат затем обрабатывается специальным цифровым фильтром, что позволяет "восстановить" (интерполировать) эти новые значения так, как если бы они были реальными. Применимы и более традиционные методы, когда для интерполяции используются различные вычислительные алгоритмы. В результате частота дискретизации увеличивается в несколько раз, что качественным образом меняет картину: становится допустимым применение аналоговых ФНЧ рядовых характеристик, что существенно упрощает технические решения АЦП и ЦАП.

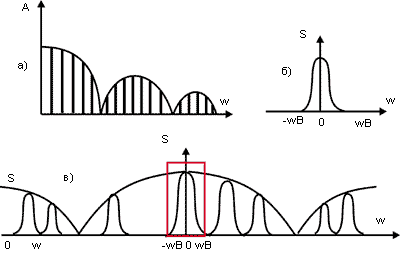
Рис 11