Выбор коэффициентов фильтра

Простейшие сглаживающие фильтры

Линейное сглаживание по трем точкам

Самым простым способом выполнения операции сглаживания будет способ, когда из трех измеренных величин вычисляется сглаживающая величина как среднее арифметическое значение:

( 1 )

Из этого выражения для N измеренных величин формируются N-2 сглаженных. При сглаживании по трем точкам усредненная измеренная величина находится в центре тяжести треугольника, построенного по этим точкам. Обычно однократного сглаживания бывает недостаточно, и применяют двукратное сглаживание:

( 2 )

Из этого выражения для N измеренных величин формируются N-4 сглаженных, что во многих случаях является допустимой потерей данных.

Сглаживание полиномом третьего порядка по пяти точкам

Для того чтобы сгладить в точке измеренную величину , необходимо через пять точек провести полином третьего порядка . Значение этого полинома в точке будет тогда выступать как сглаженная измеренная величина .

( 3 )

В системе координат, где ордината проходит через получим уравнение кубической параболы с коэффициентами от до

( 4 )

При парабола должна сглаживать пять узловых точек . Оперируя этим уравнением можно вычислить коэффициенты и соответственно сглаженную величину

( 5 )

Оперируя этой формулой, как и в случае двойного сглаживания по трем точка, нельзя сгладить две точки в начале и две в конце области измерений. В случае, когда невозможно этими значениями пренебречь, нужно определить все коэффициенты полинома (4) и получить выражения для вычисления , , и .

Синтез нерекурсивных цифровых фильтров

Преимущества нерекурсивных фильтров:

• абсолютно устойчивы;

• произвольный вид АЧХ.

• линейные ФЧХ;

Недостатки нерекурсивных фильтров:

• большой порядок при высоких требованиях к скатам АЧХ.

Особенности нерекурсивных фильтров:

• обладают конечной импульсной характеристикой ( КИХ-фильтры ).

• могут иметь постоянную задержку сигнала на выходе фильтра.

Нерекурсивный фильтр описывается:

-передаточной характеристикой

-разностным уравнением

.

Под синтезом будем понимать алгоритм определения коэффициентов фильтра, удовлетворяющих поставленным техническим требованиям частотной характеристики.

Основные методы синтеза нерекурсивных фильтров:

• рядов Фурье (взвешивания);

• частотной выборки.

1 Характеристика ких-фильтров

Частотная характеристика КИХ-фильтра :

, (8.1)

где — амплитудно-частотная характеристика фильтра;-

— Фазо-частотная характеристика фильтра;

Условие достижения линейной фазовой характеристики:

(8.2)

Решение должно удовлетворять следующим условиям:

(8.3)

• Необходима симметричная импульсная характеристика

• Порядок фильтра должен быть нечетным

Возможна реализация КИХ-фильтров:

• с нечетным порядком фильтра

• с антисимметричной импульсной характеристикой

• существует 4 вида КИХ-фильтров с линейной ФЧХ.

Рассмотрим методы синтеза фильтров 1-ого вида.

2 Синтез ких-фильтров с использованием рядов Фурье

Необходимо рассчитать коэффициенты фильтра

для достижения требуемой частотной характеристики.

Для КИХ-фильтра имеем  :

. (8.4)

Частотная характеристика фильтра может быть представлена рядом Фурье:

, (8.5)

(8.6)

Зная , можно получить отсчеты .

Однако использование отсчетов импульсной характеристики для синтеза КИХ-фильтра связано с двумя трудностями:

1. Для достижения требуемой частотной характеристики необходимо иметь бесконечное число отсчетов импульсной характеристики.

2. Фильтр физически нереализуем, так как импульсная характеристика начинается в отрицательной области значений.

• Для получения конечного фильтра положим

при .

• Для физической реализуемости осуществим сдвиг

на отсчетов.

• Усечение импульсной характеристики приводит к погрешности в достижении требуемой частотной характеристики.

Идеальная и реальная частотная характеристика.

• Эффект возникновения пульсаций называется эффектом

Гиббса.

Для пояснения эффекта Гиббса рассмотрим идеальный ФНЧ:

Найдем импульсную характеристику ФНЧ:

.

Импульсная характеристика имеет вид:

Если взять отсчетов импульсной характеристики, то частотная характеристика будет описываться выражением:

.

Реальная частотная характеристика будет иметь вид:

Определим, от чего зависит переходная полоса и уровни пульсаций и .

Усечение импульсной характеристики соответствует умножению на весовую функцию (окно) вида:

Умножение эквивалентно свертке в частотной области:

,

где — спектральная плотность окна.

• чем длиннее «окно» (больше порядок фильтра), тем уже будет спектр «окна»;

• уровень боковых составляющих будет неизменен;

• при простом усечении сужается только переходная полоса.

Весовое «окно» должно иметь минимальную ширину главного лепестка спектра, что минимизирует ширину переходной полосы , и минимальный уровень боковых лепестков спектра, что минимизирует уровень пульсаций.

Некоторое из видов «окон» и их характеристики.

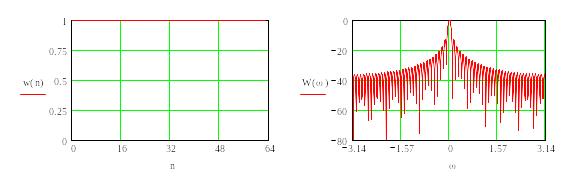
Прямоугольное окно

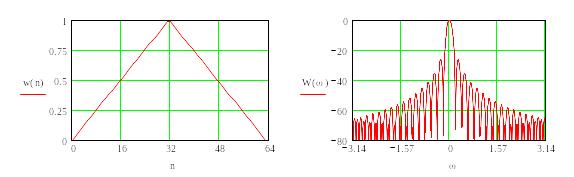
Треугольное окно

Окно Хана

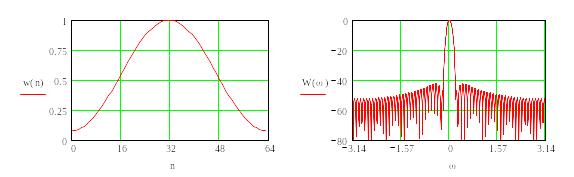
Окно Хэмминга

Окно Блэкмана

Характеристика «Оконных функций»:

Табл. 8.1.

Наименование окна	Весовая функция	Ширина спектра 	Уровень боковых лепестков
1. Прямоугольное	1		21
2. Треугольное			25
3. Ханна			44
4. Хэмминга			53
5. Блэкмана			58

Аналитическое описание импульсных характеристик:

Табл. 8.2.

Тип фильтра	Импульсная характеристика
ФНЧ
ФВЧ
ППФ
ПЗФ