Формы реализации дискретных фильтров
Структурная схема, показанная ранее на рис. 4.4, называется прямой формой реализации рекурсивного фильтра (direct form I) и не является единственно возможной. Рассмотрим еще несколько вариантов.
Каноническая форма
Разделим общий сумматор в схеме рис. 7 на два отдельных — для рекурсивной и нерекурсивной частей фильтра (рис. 8, а). В результате получаем два последовательно соединенных фильтра, один из которых является нерекурсивным, а другой, напротив, содержит только рекурсивную часть. Так как результат последовательного прохождения сигнала через ряд линейных стационарных устройств не зависит от последовательности их соединения, мы можем поменять местами две «половинки» нашего фильтра (рис. 8, б). Теперь остается заметить, что в обе линии задержки подается один и тот же сигнал, поэтому они будут содержать одинаковые наборы отсчетов. Это позволяет объединить линии задержки. Полученная в результате схема изображена на рис. 9, она называется канонической формой реализации рекурсивного фильтра (canonic form или direct form II).
С теоретической точки зрения эти варианты эквивалентны. Однако при практической реализации необходимо обратить внимание на ряд особенностей, присущих этим схемам. С одной стороны, при канонической реализации используется общая линия задержки, что уменьшает число необходимых ячеек памяти. Однако при этом абсолютные величины отсчетов, «бегающих» в линии задержки, могут существенно превосходить амплитуду входного и выходного сигналов. Это приводит к необходимости увеличивать разрядность представления чисел в линии задержки по сравнению с разрядностью входного и выходного сигналов, что усложняет реализацию устройства. При прямой реализации в линиях задержки хранятся непосредственно отсчеты входного и выходного сигналов, то есть повышенная разрядность линий задержки не требуется. Единственным элементом, требующим повышенной разрядности, в данном случае является сумматор, и это учтено в архитектуре микропроцессоров, специально предназначенных для обработки сигналов в реальном времени.
Рис. 8. Перестановка рекурсивной и нерекурсивной частей фильтра путь к получению канонической реализации
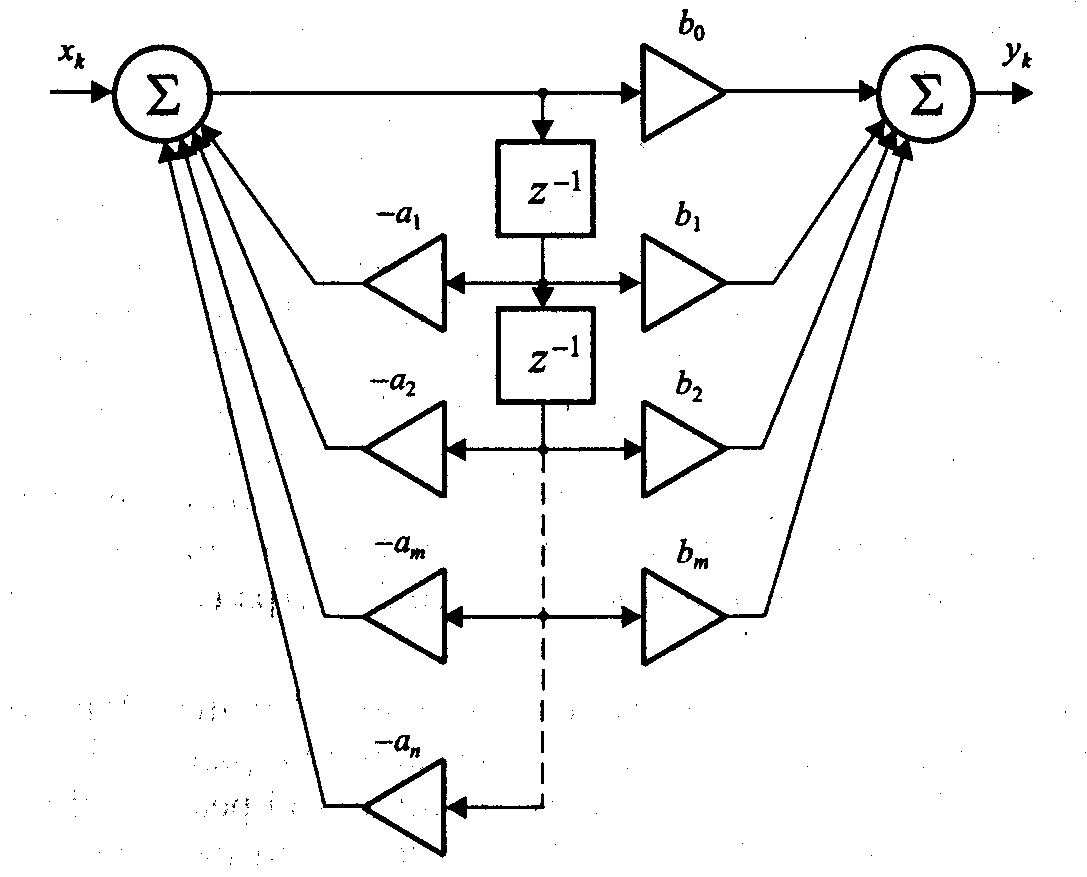
Рис. 9. Рекурсивный фильтр — каноническая реализация
ЗАМЕЧАНИЕ —-----------------------------------------------------------------------------------------
Представление дискретной системы в пространстве состояний соответствует именно канонической форме реализации. Вектор состояния при этом представляет собой набор значений выходов элементов задержки.
Транспонированная форма
Поменяем в схеме рис. 6 последовательность выполнения операций умножения и задержки, используя в каждой ветви отдельную линию задержки на нужное количество тактов. Разделим также общий сумматор на несколько двух-входовых сумматоров. Получившаяся структура показана на рис. 10. Теперь, рассмотрев любую пару соседних сумматоров, можно заметить, что суммируемые ими сигналы претерпевают некоторую общую задержку. Это дает возможность поменять местами операции суммирования и задержки. Получившаяся схема, показанная на рис. 11, называется транспонированной реализацией дискретного фильтра (direct transposed form II).
ЗАМЕЧАНИЕ--------------------------------------------------------------------------------------------------
Разумеется, в транспонированной форме может быть реализован и нерекурсивный фильтр. Для этого в структурной схеме рис. 10 необходимо удалить все ветви с коэффициентами bt, кроме bo.
Транспонированная схема позволяет эффективно распараллелить вычисления и потому применяется при реализации дискретных фильтров в виде специализированных интегральных схем. Действительно, при реализации фильтра в форме рис. 4.3 или рис 4.4 можно одновременно выполнять все операции умножения, но для получения выходного результата необходимо дождаться окончания выполнения всех операций сложения. В транспонированной же схеме, помимо умножения, можно одновременно выполнять и все операции сложения, поскольку они являются независимыми (то есть не используют в качестве суммируемых величин результаты других сложений).
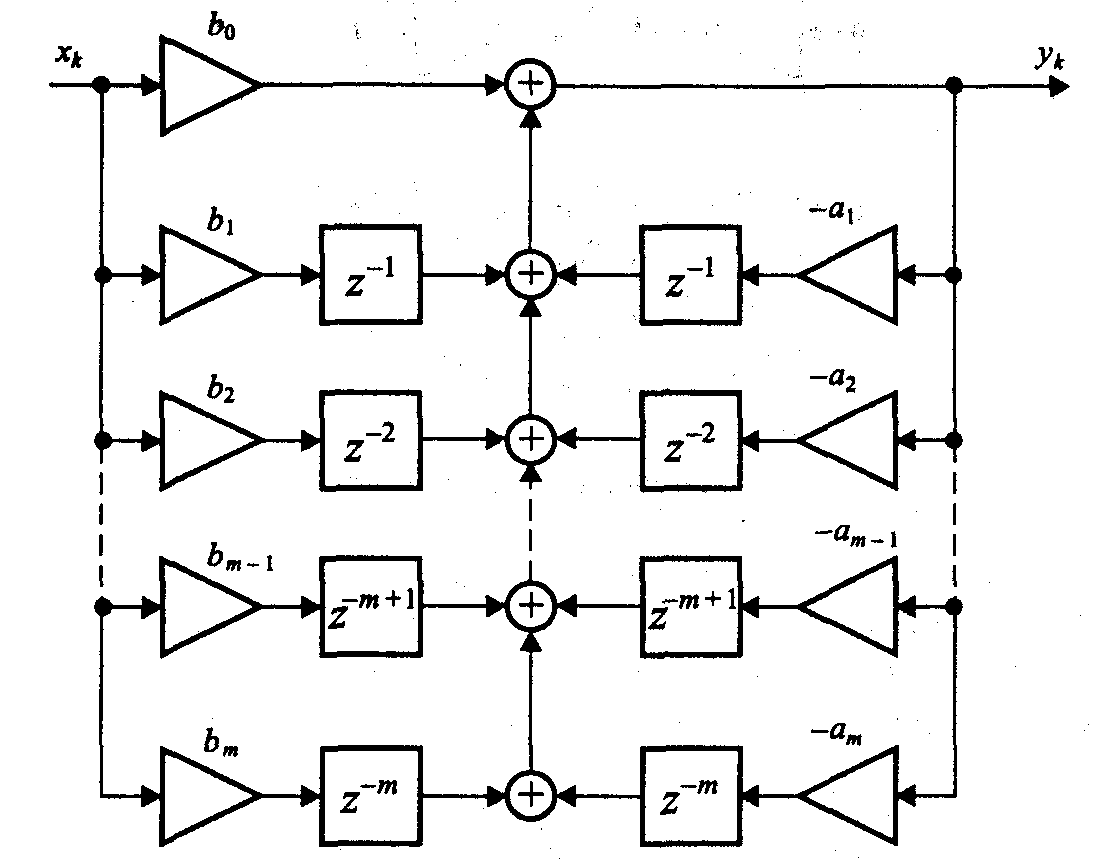
Рис. 10. Изменение последовательности выполнения операций умножения и задержки — путь к получению транспонированной реализации фильтра
Как видно из схемы рис. 10, собственно для расчета выходного сигнала необходимо выполнить одно умножение и одно cложение; все остальные операций производят подготовку промежуточных результатов для вычисления последующих выходных отсчетов.
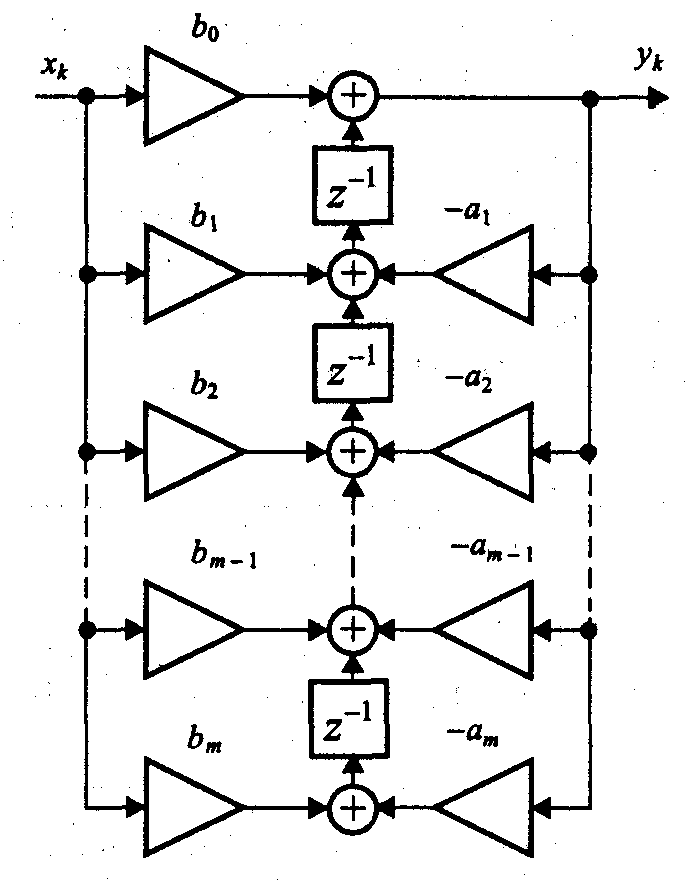
Рис. 11. Транспонированная реализация дискретного фильтра
Если применить описанные преобразования к канонической структуре, показанной на рис. 9, получится еще один вариант транспонированной реализации фильтра (direct transposed form I) (рис. 12). В отличие от предыдущей схемы, данная структура содержит большее число элементов памяти.
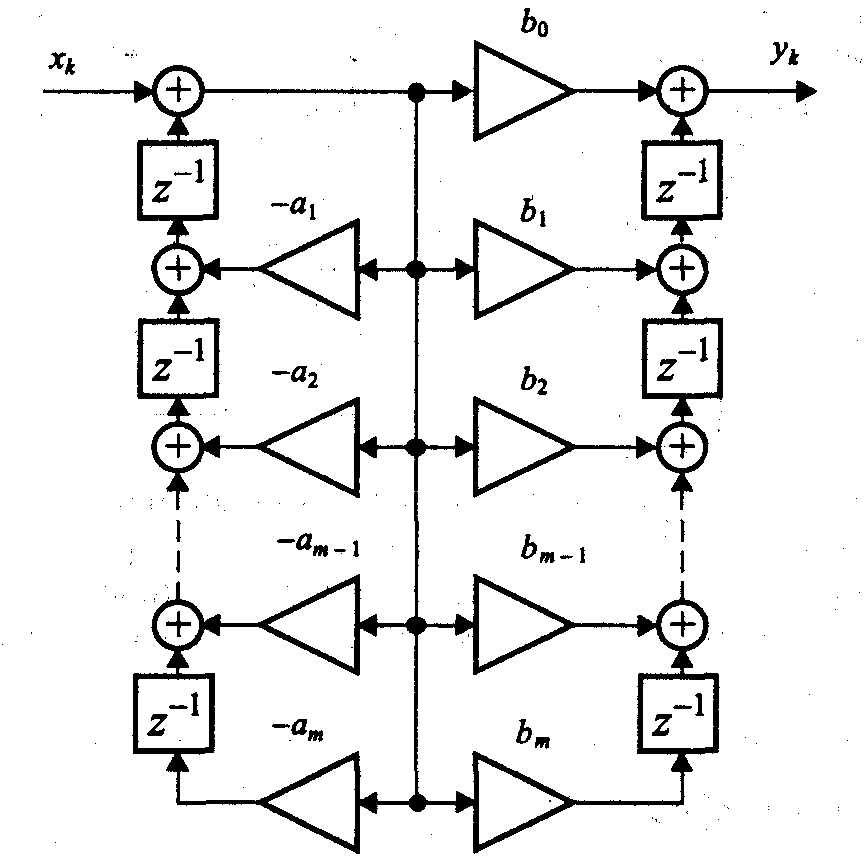
Рис. 12. Транспонированная реализация, полученная из канонической формы дискретного фильтра
Последовательная (каскадная) форма
В разделе «Нули и полюсы» было показано, что числитель и знаменатель функции передачи физически реализуемого дискретного фильтра можно разложить на линейные (относительно ) множители. Перемножение функций передачи соответствует последовательному (каскадному) включении} соответствующих фильтров, поэтому такое представление дает реализацию фильтра в виде последовательно включенных фильтров 1-го порядка (при этом некоторые из них могут иметь комплексные коэффициенты) либо фильтров 1-го и 2-го порядка с Вещественными коэффициентами.
Рассмотрим конкретный пример, задавшись чйслёйными значениями коэффициентов фильтра:
(4.16)
ЗАМЕЧАНИЕ---------------------------------------------------------------------------------------------------
Данный фильтр является фильтром Баттерворта 3-го порядка с частотой среза, равной 1/5 частоты дискретизации, синтезированным методом билинейного z-преобразования.
Структурная схема получившейся последовательной реализации фильтра представлена на рис. 13.
Рис.13. Последовательная реализация дискретного фильтра
Последовательная реализация часто используется на практике, поскольку она позволяет ослабить нежелательные эффекты, связанные с ошибками округления.
Параллельная форма
Еще один способ; преобразования функциц, передачи фдаиче(;ки реализуемого фильтра — представление ее в виде суммы простейших дробей. Каждое из слагаемых при таком представлении соответствует функции передачи рекурсивного фильтра 1-го порядка (возможно, с комплексными коэффициентам) либо 1-го или 2-го порядка (если используется представление в виде суммы простейших дробей только с вещественными коэффициентами). Сама операция сложения эквивалентна параллельному соединению этих фильтров с суммированием выходных результатов;
Рассмотрим конкретный пример, используя ту же функцию передачи (4.16), что и раньше:
Структурная схема получившейся параллельной реализации фильтра представлена на рис. 14. Постоянному слагаемому соответствует верхняя ветвь структурной схемы, содержащая только умножитель.
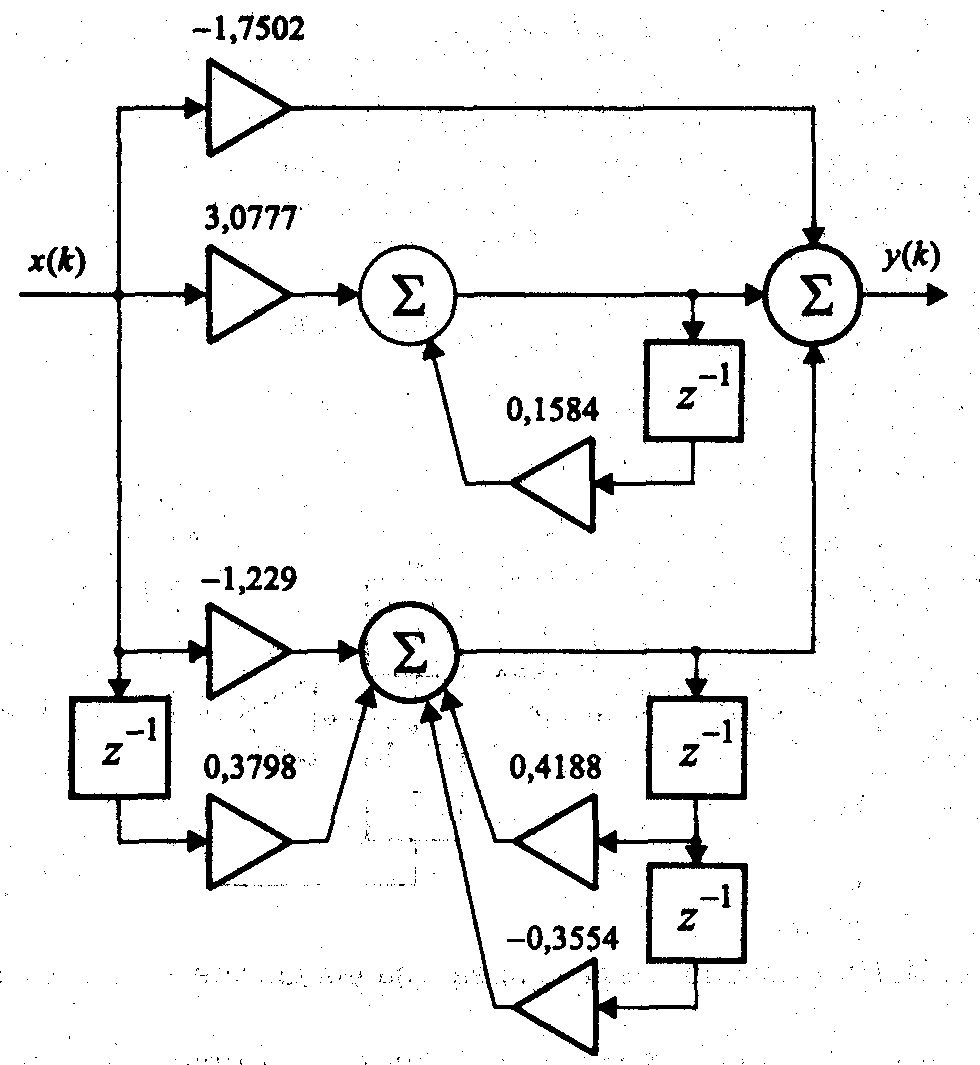
Рис. 14. Параллельная реализация дискретного фильтра