Теоретические сведения

Назначение и типы фильтров

Фильтры — это электрические цепи, целенаправленным образом изменяющие спектры сигналов. Фильтрация сигнала, т. е. изменение его спектра, обычно предпринимается с целью увеличить отношение полезного сигнала к шумам и помехам или подчеркнуть (усилить) какие-нибудь полезные качества сигнала.

Например, при измерении сигналов, получаемых от термопар, чаще всего приходится применять фильтры, ослабляющие помехи от системы силового электропитания. Выходной полезный сигнал термопар составляет, как правило, несколько милливольт, и помеха от силовой сети, имеющая частоту 50 Гц, может быть сравнимой с полезным сигналом или даже превосходить его. Шумы измеренных величин и случайные погрешности измерительного прибора порождают в общем случае рассеивание измеренных величин . Поэтому рациональнее сгладить их перед дальнейшей обработкой, т. е. усреднить. По своей сути сглаживание, как одна из операций предварительной обработки информации, выполняет роль цифрового фильтра, который подавляет высокочастотные (быстрые) колебания в исходном сигнале.

Другой пример — фильтрация сигнала, получаемого от датчика момента, развиваемого двигателем некоторого транспортного средства. Выделяя с помощью фильтра постоянную составляющую этого сигнала, мы получаем информацию о средней мощности двигателя. Если же выделить и проанализировать высокочастотные составляющие сигнала, то можно сделать вывод о качестве работы системы регулирования, о вибрации, обусловленной работающим двигателем, и т. п.

Теория фильтрации сигналов и методы построения фильтров в настоящее время весьма развиты. Существует очень большое число различных видов фильтров. Классификация фильтров может быть проведена по различным признакам. Далее рассматриваются линейные стационарные фильтры. Мы будем использовать при разделении фильтров по группам четыре различных признака, указанные ниже.

Первый признак — вид входного и выходного сигнала фильтра. Если эти сигналы аналоговые, то фильтр называется аналоговым, если же сигналы представлены цифровым кодом, то фильтр называется цифровым. Возможны и промежуточные варианты: аналого-цифровой фильтр (вход аналоговый, выход цифровой) и цифроаналоговый (вход цифровой, выход аналоговый).

Второй признак — вид частотной характеристики. По этому признаку фильтры делятся на следующие группы: фильтры нижних частот (ФНЧ) пропускают низкочастотные составляющие спектра и задерживают высокочастотные; фильтры верхних частот (ФВЧ) пропускают только высокочастотные составляющие; фильтры полоснопропускающие (ФПП) пропускают составляющие сигнала только в определенной полосе частот; фильтры полосно-заграждающие (ФПЗ) пропускают все составляющие сигнала, за исключением тех, частоты которых входят в определенную полосу; фильтры всепропускающие (ФВП) пропускают все без исключения составляющие сигнала, но изменяют фазовые соотношения между ними. Графики АЧХ упомянутых видов фильтров показаны на рис. 1, а, б, в, г, д. Кроме перечисленных, основных по этому признаку, групп, есть и другие разновидности. Например, резонансный фильтр представляет собой частный случай полосно-пропускающего фильтра, но с очень узкой полосой пропускания (штриховая АЧХ на рис. 1, г). Фильтр-пробка на определенную частоту—это ФПЗ с узкой полосой заграждения (штриховая АЧХ на рис. 1, г). Гребенчатый фильтр — это такой фильтр, который имеет несколько полос пропускания (рис. 1, е). В название фильтра входит обычно та частотная полоса, которую фильтр пропускает. Так, фильтр нижних частот — это фильтр, пропускающий нижние частоты сигнала. Поэтому не совсем корректны встречающиеся иногда словосочетания типа «фильтрация помех». Фильтруется, т. е. проходит через фильтр, полезный сигнал, а помеха задерживается, не пропускается.

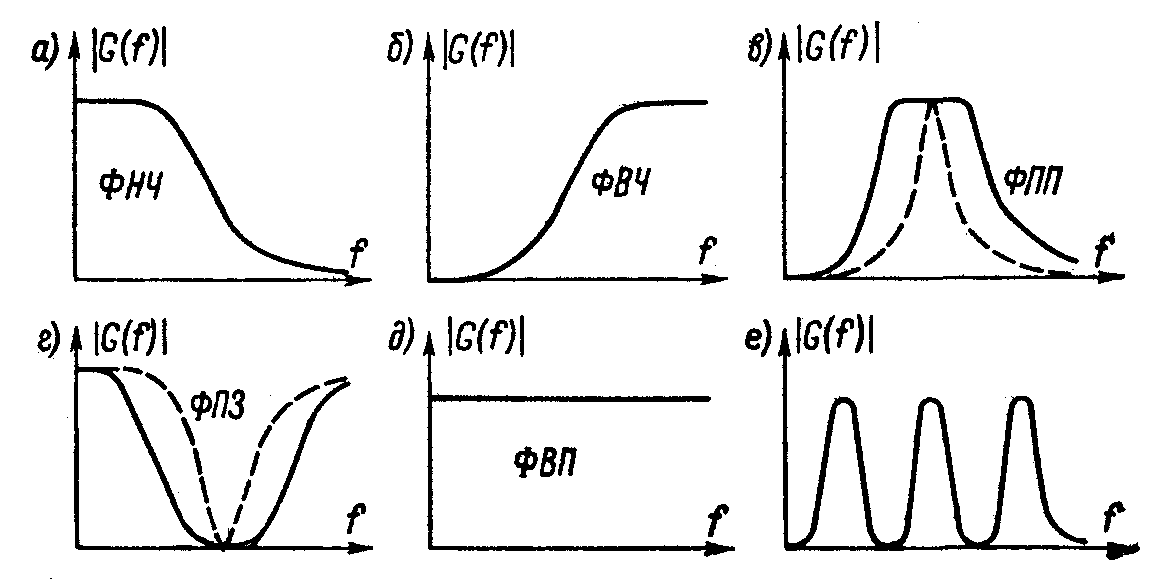
Рис. 1. Амплитудно-частотные характеристики различных фильтров

Отметим, что в качестве базового при анализе и синтезе фильтров обычно принимается фильтр нижних частот. Именно ФНЧ, как правило, рассматривается в различных публикациях, для него разрабатываются методики синтеза. Остальные же виды фильтров могут быть построены на основе ФНЧ. Так, если из полного сигнала вычесть выходной сигнал ФНЧ, то в итоге мы получим ФВЧ (рис. 2, а). ФПЗ можно построить, если включить параллельно ФНЧ и ФВЧ с разными частотами среза (рис. 2,6). Для построения ФПП достаточно соединить последовательно соответствующим образом рассчитанные ФНЧ и ФВЧ.

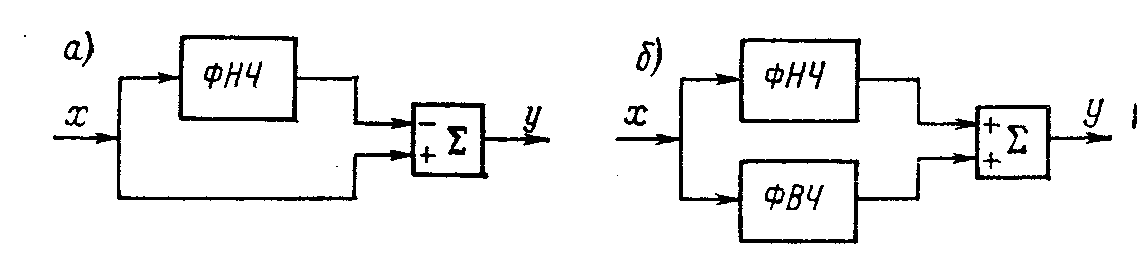
Рис. 2. Возможные структуры фильтра верхних частот (а) и полосно-заграждающего фильтра (б)

Третий признак— это вид их импульсных характеристик. Непрерывный фильтр — это фильтр с непрерывной ИХ, дискретный фильтр — это фильтр, ИХ которого представлена набором -импульсов. Наконец, импульсный фильтр имеет ИХ, состоящую из последовательности одинаковых по форме импульсов конечной длительности разной амплитуды. В принципе возможны фильтры, при классификации которых по данному признаку возникают некоторые затруднения, но такие фильтры на практике встречаются редко.

Четвертый признак — это протяженность импульсной характеристики. Если ИХ финитна, т. е. ограничена во времени, то такие фильтры называют фильтрами с конечной импульсной характеристикой или коротко КИХ-фильтрами. Если ИХ, хотя и затухает со временем, но имеет теоретически не ограниченную во времени протяженность, то соответствующий фильтр называют БИХ-фильтром, т.е. фильтром с бесконечной импульсной характеристикой.

Рис. 3. Примеры импульсных характеристик: импульсного КИХ-фильтра (а) и дискретного БИХ-фильтра (б)

Дискретные фильтры

^{Дискретный фильтр – это произвольная система обработки дискретного сигнала, обладающая свойствами линейности и стационарности. Под этими свойствами понимается: линейность означает, что выходная реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности, а стационарность – что задержка входного сигнала приводит лишь к такой же задержке выходного сигнала, не меняя его формы.}

При сглаживании функции по i точкам, следует различать две возможные ситуации:

1) Данные(отсчеты сигнала) уже все есть и для вычисления усредненного отсчета y_n берутся отсчеты сигнала слева и справа, например формула (1) {x_n-(i-1)/2,… x_n,… x_n+(i-1)/2}. Метод применяется при анализе ранее полученных и сохраненных данных (условно назовем этот процесс сглаживанием).

2) Данные поступают с внешнего устройства, следовательно «правых» отсчетов сигнала на графике не существует и для вычисления усредненного отсчета y_n берутся отсчеты сигнала слева {x_n-i,… x_n}. Данный метод называется(является) «физически реализуемым», т.к. соответствует работе реальных устройств (условно назовем этот процесс фильтрацией). Следует отметить, что при рассмотрении цифровых фильтров принято считать, что данные поступают и сдвигаются слева на право, т.е ноль графика функции расположен справа.

В общем случае дискретный фильтр суммирует (с весовыми коэффициентами) некоторое количество входных отсчетов (включая последний) и некоторое количество предыдущих выходных отсчетов:

, (*)

где a_j и b_i – вещественные коэффициенты.

Такой фильтр называется рекурсивным. Фильтр, суммирующий только некоторое количество входных отсчетов называется нерекурсивным.