16.Основные правила дифференцирования, табл производных, логарифмическое дифф.
правила
дифференцирования:Пусть
u
=
u
(x)
и
v
=
v(x)
-дифференцируемые
функции независимой переменной x;
c
= const.
Тогда:
;
;
;.
Таблица
производных:
Логарифмическое
диференцирование:Логаривмируем
функцию:
Дифференцируем:
Выражаем
y’
из полученного соотношения:
17.Производные основных элементарных функций.
Производные_основных
элементарных функцийСтепенная_функция
Дадим
аргументу x
приращение ∆ х. Функция
получит
приращение
.
По формуле бинома Ньютона имеем:
Тогда
Находим предел составленного отношения при ∆х→0:
Таким
образом,
Показательная_функция
Найдем
сначала производную функции
.
Придав аргументу х приращение ∆х,
находим приращение функции ∆у:
и
При вычислении предела воспользовались
эквивалентностью
~
х при х → 0.
Итак,
,
т.е.
Теперь
рассмотрим функцию
Так_как
то по формуле производной сложной
функции находим:
Таким
образом,
Логарифмическаяфункция
Найдем
производную функции
Для_нее
Переходя
к пределу при ∆х → 0 и воспользовавшись
эквивалентностью
~
при ∆х → 0, получаем:
т.е.
.
Теперь
рассмотрим функцию
Так как
то
Таким_образом,
Тригонометрические функции y = sinx, y = cosx, y = tgx, y= ctgx
Для функции y = sinx имеем:
Переходя
к пределу при ∆х → 0 и воспользовавшись
первым замечательным пределом
получаем
т.е.
y = cosx:
.y
= tgx:
y
= ctgx:
Обратныетригонометрическиефункцииy = arcsinx, y = arccosx, y = arctgx, y= arcctgx
Пусть
y
= arcsinx.
Обратная ей функция имеет вид х = sin
у,
На интервале
верно равенство
По
правилу дифференцирования обратных
функций
где перед корнем взят знак плюс, так как
cosy>
0 при
Аналогично
получаем, что
y = arctgx является обратной к функции х = tg у, где
y = arcсtgx:
Функции
arctgx
и arctgx
связаны отношением
18.Гиперболические функции и их производные.
.Гиперболические функции и их производные
− гиперболический
синус;
− гиперболический косинус («цепная
линия»);
и
− гиперболический тангенс и котангенс,
где е – неперово число.
Найдем производные гиперболических функций:
19.Производные высшего порядка.Дифф.неяно и параметрически заданных функций.
20.Производная сложной функции и производная обратной функции.
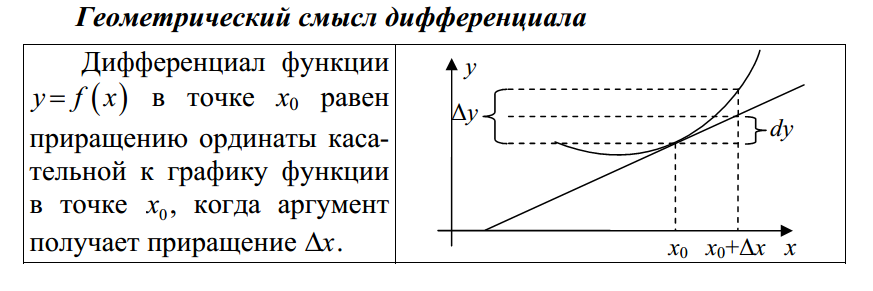
21.Дифф.функции.Геометрический смысл производной и дифференциал.
22.Инвариантность формы первого дифференциала. Дифференциалы высшего порядка.
Инвариантность формы первого дифференциала:
Дифферинциал
функции z=g(y)
в точке y0
имеет вид:dz=g’(y0)dy,где
dy
-дифференциал
тождественного отображения yày0:dy(h)=h,
h
R.Пусть
теперь y=f(x),
x
U(x0),
f
D(x0).
Тогда dy=f’(x0)dx,
и согласно цепном
правилу:
dz=g’(f(x0))×f’(x0)dx=g’(y0)dy.Таким
образом, форма первого дифференциала
остаётся одной и той же вне зависимости
от того, является ли переменная функцией
или нет.
Дифференциалы высших порядков:
Дифференциалом порядка n,
где n
> 1, от функции 
в некоторой точке называется дифференциал
в этой точке от дифференциала порядка (n —
1), то есть