7. Сравнение бмф. Эквивалент бмф и их применение при нахождении пределов .

Сравнение бесконечно малых функций производится путем нахождения предела их отношения. Пусть α (x) и β (x) – бмф при x → a, причем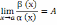 Тогда если: 1) А = 1, то α (x) и β (x) называются эквивалентными бмф при x → a, что записывается в виде α (x) ~ β (x); 2) A ≠ 0и A ≠∞, то α (x) и β (x) – бмф одного порядка малости при x → a; 3) A = 0, то β (x) есть бмф более высокого порядка малости, чем α (x), при x → a, что записывается в виде β (x) = o (α(x)); 4) A =∞, то α (x) есть бмф более высокого порядка малости, чем β (x), при x → a, что записывается в виде α (x) =o (β (x)).Свойства бесконечно малых функций 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бмф. 2. Произведение бесконечно малой функции на ограниченную функцию есть бмф. 3. Если α (x) ~ β (x) , то β (x) ~ α (x) . 4. Если α (x) ~ β (x) и β (x) ~γ (x) , то α (x) ~γ (x) .5. Если α (x) ~ β (x) , то α (x) − β (x ) = o (α(x)) = o (β(x) ) .6. Если α (x) ~ α′ (x) и β (x) ~ β ′ (x), то 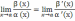.Пример. Рассмотрим функции , ,

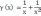
Тогда α (x)– бмф при x →∞, β (x)– бмф при x→∞, γ (x) – бмф при x→∞.Частное есть функция бесконечно большая при x→∞;Частное 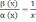есть бмф при x→∞;Частное 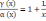есть функция, имеющая конечный предел при x→∞.

8.Первый замечательный предел

Примеры.При раскрытии неопределенностей вида с выражениями, содержащими тригонометрические функции, часто используется предел 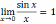,называемый первым замечательным пределом.Пример. Вычислить пределы: 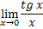, 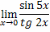Решение.1)

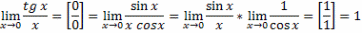
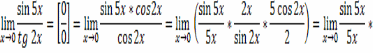
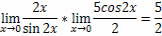
9.Второй замечательный предел

При раскрытии неопределенности вида [1∞] часто используется предел вида

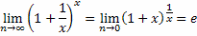
называемый вторым замечательным пределом, число е – предел числовой последовательности 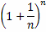, n = 1,2,3… – является числом иррациональным, е= 2,718281828459045... .

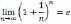Число е играет важную роль в математическом анализе. Показательная функция с основанием е (y=e^x ) называется экспонентой. Логарифм по основанию е называется натуральным (или неперовым) логарифмом и обозначается ln x. Таким образом,

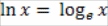
Из второго замечательного предела можно получить пределы, которые широко применяются для раскрытия неопределенностей:

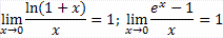
Пример. Вычислить пределы:

1)

Решение.1) =

=

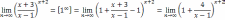10. Определение непрерывности функции в точке. Основные теоремы о непрерывности в точке

Определение непрерывности функции в точке:Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки.Функция y=f(x) называется непреывной в точке x_0,если существует предел функции в этой точке и он равен значению функции в этой точке,т.е limf(x)=f(x₀)(при x стремящимся к x₀)

Основные теоремы о непрерывности функциях

.1)Сумма,произведение и частное двух непрерывных функций есть функция непрерывная(для частного за исключением тех значений аргумента,в которых делитель равен нулю).

2)Пусть функция u=бэтта от x непрерывна в точке х_0,а функция y=f(u) в точке u₀=бэтта от x₀.Тогда сложная функция f(бэтта(х)),состоящая из непрерывных функций,непрерывна в точке x_0.

3)Если функция y=f(x) непрерывна и строго монотонна на [a;b] оси Ox,то обратная функция y=бэтта(x) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Oy(без доказательства)