81.Поверхности уровня. Уравнение касательной плоскости к поверхности.
Поверхность уровня функции u=f(х, у, z) или поверхность уровня скалярного поля — поверхность, задаваемая уравнением f (х, у, z)=С, где С — постоянная. В точках поверхности уровня функция принимает заданное постоянное значение u = С.
Пусть М – точка поверхности S. Плоскость, содержащая точку М и обладающая тем свойством, что расстояние от этой плоскости до переменной точки M1 поверхности S является бесконечно малым по сравнению с расстоянием ММ1, называется касательной плоскостью к поверхности S в точке М.
Если
поверхность в трехмерном пространстве
задана уравнением f(x;
y;
z)
= 0, где функция f
достаточное число раз дифференцируема,
то уравнение плоскости, касательной к
этой поверхности в точке
,
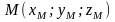имеет вид:
,
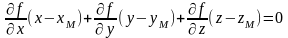где
–
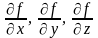частные производные функции трех
переменных f(x;
y;
z)
по этим переменным.
Если же поверхность задана уравнением,
разрешенным относительно аппликаты z,
т.е. имеет вид z
= z(x;
y),
то уравнение касательной плоскости
принимает вид: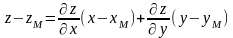
82.Касательная плоскость и нормаль к поверхности.
Пусть функция z= f(x;y) дифференцируема в точке (х0; y0) некоторой области D єR2 . Рассечем поверхность S, изображающую функцию z, плоскостями х = х0 и y= y0. Плоскость х = х0 пересекает поверхность S по некоторой линии z0 (у), уравнение которой получается подстановкой в выражение исходной функции z= f(x; y) вместо х числа х0. Точка М0(x0; y0; f(x0; y0))принадлежит кривой z0(y) в силу дифференцируемости функции zв точке М0 функция z0 (y) также является дифференцируемой в точке y=y0. Следовательно, в этой точке в плоскости х = x0 к кривой z0(y) может быть проведена касательная l1. Проводя аналогичные рассуждения для сечения y= y0, построим касательную l2к кривой z0 (x) в точке х = x0. Прямые l1и l2определяют плоскость а, которая называется касательной плоскостью к поверхности S в точке М0 . Уравнение: z- z0=f’(x0; y0)*(x - х0) + f’(x0; y0)*(y - y0).
Прямая,
проходящая через точку М0
и перпендикулярная касательной плоскости,
построенной в этой точке поверхности,
называется ее нормалью. Канонические
уравнения нормали:
.
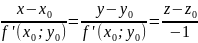83.Экстремумы функций двух переменных.
Пусть функция z = f(x; y) определена в некоторой области D, точка N(x0;y0) єD. Условия экстремума. Если в точке N(x0; y0) дифференцируемая функция z = f(x; y) имеет экстремум, то ее частные производные в этой точке равны нулю: f’(x0;y0) =0, f’(x0;y0) = 0. Точка, в которой частные производные первого порядка функции z = f(x; y) равны нулю, т. е. f’x= 0, f’y= 0, называется стационарной точкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими. В критических точках функция может иметь экстремум, а может и не иметь. Пусть в стационарной точке (x0;y0) и некоторой ее окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х0; y0) значения А= f”xx(x0; у0), В == f”xy(x0; у0), С = f”yy(x0; y0). Обозначим
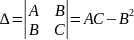
Тогда:
1) если ∆ >0, то функция f(x; y) в точке (х0; y0) имеет экстремум: максимум, если А<0; минимум, если А >0;
2) если ∆ <0, то функция f(x; y) в точке (x0;y0) экстремума не имеет.
3)В случае ∆ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования.