
- •1Множества:определение, основные числовые множества. Операции над множеством
- •2. Способы задания функции одной переменной.Классификация функций
- •3. Функция как отображение,множество определения и значений график функции.Сложная функция. Определение и свойства обратной функции.
- •4. Открытые множества на прямой ,плоскости и в пространстве. Окрестность точки. Определение предела функции. Свойство пределов.
- •5. Предел функции одной переменной на языке окрестности
- •6.Бесконечно малые и бесконечно большие функции.
- •7. Сравнение бмф. Эквивалент бмф и их применение при нахождении пределов .
- •8.Первый замечательный предел
- •9.Второй замечательный предел
- •10. Определение непрерывности функции в точке. Основные теоремы о непрерывности в точке
- •11. Условие непрерывности в точке функции одной переменной. Классификация точек разрыва. Непрерывность элементырных функций.
- •12.Свойство функций непрерывных на замкнутом промежутке.
- •13.Задачи приводящие к понятию производной.
- •14.Производная и ее связь с дифференциалом,геометрический и механический смысл. Уравнение касательной.
- •15.Дифференцируемость функции, связь с непрерывностью. Линеаризация и ее геометрический смысл.
- •16.Основные правила дифференцирования, табл производных, логарифмическое дифф.
- •17.Производные основных элементарных функций.
- •23.Теорема Ферма. Необходимое условие локального экстремума.
- •24.Теорема Ролля.
- •25.Теорема Лангранжа и Коши
- •30.Локальные экстремумы функции. Нахождение наибольшего и наименьшего значения функции на замкнутом промежутке.
- •31.Выпуклые и вогнутые функции. Точки перегиба и их нахождения.
- •32.Асимптоты графика функции.
- •33.Общая схема иследования функции и построение ее графика.
- •34.Комплексные числа.
- •35.Действия над комплексными числами. Извлечения корня n-ой степени из комплексного числа.
- •36.Понятие о функции комплексной переменной.
- •37.Неопределенный интеграл и его основные функции. Табл интеграллов.
- •39.Интегрирование по частям.
- •40.Интегрирование простейших рациональных функций.
- •41.Алгоритм интегрирования рациональных функций.
- •43.Метод рационализации при интегрировании простейших иррациональных функций.
- •44.Интеграл типа
- •45.Матрицы.Основные понятия и действия над матрицами.
- •46.Определители второго и третьего порядка,их вычисления и основные свойства.
- •47.Определение условие существования и вычисления обратной матрицы.
- •48.Решение систем линейных алгебраических уравнений по правилу Крамера.
- •49.Ранг матрицы.Решение уравнений методом Гаусса.
- •50.Понятие Векторных функций скалярного аргумента их непрерывность.
- •51.Векторы на плоскости и в пространстве и линейные операции над ними.
- •52.Линейные зависимости и независемость вектаров.Базис.
- •53.Координаты вектора.Векторное пространство.
- •54.Проекция вектора на ось.Свойства проекции.
- •55.Скалярное произведение векторов.
- •56.Выражение скалярного произведения через координаты сомножителей.
- •57.Векторное произведение векторов.Основные свойства.
- •63.Различные виды уравнения прямой на плоскости. Угол между прямой.
- •64.Взаимное расположение двух прямых на плоскости. Условие параллельности и Перпендикулярности.
- •65.Полярные координаты.Связь с декартовыми.
- •66.Эллипс.
- •67.Гипербола.
- •68.Парабола.
- •69.Различные виды уровнения и перпендикулярности прямых.Угол между прямыми.
- •70.Условие параллельности и перпендикулярности прямых. Скрещивающиеся прямые.
- •71.Различные виды уравнения плоскости в пространстве. Угол между плоскостями.
- •72.Условие параллельности и перпендикулярности плоскостей. Расстояние от точки до плоскости.
- •73.Угол между прямой и плоскостью условие параллельности и перпендикулярности прямой и плоскости.
- •74. Поверхность в пространстве. Поверхности вращения, цилиндрические, конические и их примеры.
- •75. Поверхности второго порядка и их классификация.
- •76.Определение функции нескольких переменных.
- •77.Частные производные и частные дифференциалы фнп.
- •78.Производные сложных и неявно заданных функций. Примеры.
- •79. Понятие дифференцируемости функций двух переменных. Полный дифференциал.
- •81.Поверхности уровня. Уравнение касательной плоскости к поверхности.
- •83.Экстремумы функций двух переменных.
- •84.Нахождение наибольшего и наименьшего значения на компакте. Понятие об условном экстремуме.
53.Координаты вектора.Векторное пространство.
Обычно
на плоскости(в пространстве) в качестве
базисных векторов берут декартовы орты
декартовы единичные векторы i͢j
–на плоскости i͢jk͢͢
- в пространстве.
Координаты вектора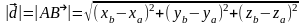 Векторное
пространство Rn
Векторное
пространство Rn
Множество векторов на плоскости и в пространстве , заданных своими координатами, с линейными операциями покоординатного сложения и умножения на числа допускает естественное обобщение на случай n координат, когда векторы рассматриваются как элементы n-мерного (числового) пространства Rn. Обычно пространство Rn отождествляется с множеством матриц-столбцов размера n×1 со стандартными операциями сложения матриц и умножения их на числа: Rn= Rn+1 .
54.Проекция вектора на ось.Свойства проекции.
Проекция вектора α на ось l наз. число, равное произведению модуля вектора на косинус угла между вектором и осью; обозначается прlα.
Тогда прoxOM=|OM|cosα=x, прoyOM=|OM|cosβ=y.
Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол- прямой.
Проекции равных векторов на одну и ту же ось равны между собой.
Свойства проекций
,
![]()
.![]() ,
где
,
где![]()
Если![]() ,
,![]()
![]() ,
,![]()
Проекция
суммы векторов на ось![]() равна
сумме проекций векторов на
равна
сумме проекций векторов на
55.Скалярное произведение векторов.
Скалярное
произведение векторов
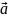 и
и
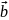 это произведение модулей этих векторов
на косинус угла
это произведение модулей этих векторов
на косинус угла
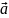 ^
=ϕ
между ними:
^
=ϕ
между ними:
 Если
векторы заданы в прямоугольной декартовой
системе координат
Если
векторы заданы в прямоугольной декартовой
системе координат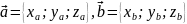 , то
, то
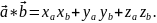
Свойства:
1).
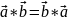
2).
 =
=

3).
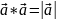 2
2
4)

Пример:
Две силы
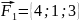 и
и
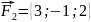 приложены в точке М
приложены в точке М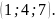 Вычислить работу их равнодействующей
Вычислить работу их равнодействующей
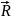 по перемещению материальной точки из
М в N(3;8;5).
Решение:
Найдём координаты равнодействующей
сил
и вектора перемещения
по перемещению материальной точки из
М в N(3;8;5).
Решение:
Найдём координаты равнодействующей
сил
и вектора перемещения
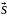 =
=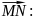
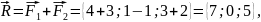
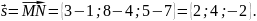
Тогда
работа равна A=
56.Выражение скалярного произведения через координаты сомножителей.
Некоторые приложения скалярного произведения:
1) условие ортогональности (перпендикулярности) ненулевыхвекторов:
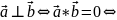 xaxb+yayb+zazb=0;
xaxb+yayb+zazb=0;
2) косинус угла между двумя ненулевыми векторами равен:
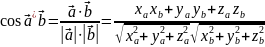 ;
;
3)
работа A
постоянной
по величине и направлению силы
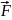
по
перемещению материальной точки на
вектор
равнаA
=
 (физический смысл скалярного произведения).
(физический смысл скалярного произведения).
57.Векторное произведение векторов.Основные свойства.
Три
некомпланарных, упорядоченных вектора
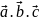 приведенные к общему началу, называют
правой
тройкой
векторов, если кратчайший поворот от
k
виден
из конца вектора
приведенные к общему началу, называют
правой
тройкой
векторов, если кратчайший поворот от
k
виден
из конца вектора
 противхода
часовой стрелки.
противхода
часовой стрелки.
Если же этот поворот виден по ходу часовой стрелки, то тройка векторов называется левой.
Декартов
базис
 образует
правую тройку.
образует
правую тройку.
Векторным произведением вектора на называетсявектор
=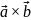 ,
обладающий свойствами:
,
обладающий свойствами:
1)
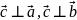 ;
;
2)
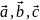 образуют правую тройку;
образуют правую тройку;
3)
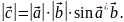
Свойства векторного произведения
1.
Если
то

2.
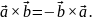
3.
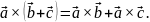
4.
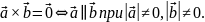
5.
Площади параллелограмма и треугольника
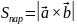
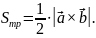
Пример.
Найти единичный вектор
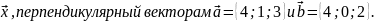
Решение.
Вектор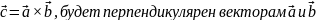 .
Найдем его:
.
Найдем его:
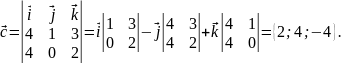
Модуль
вектора
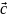 равен
равен

Следовательно,
единичные векторы, перпендикулярные
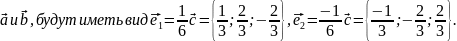
58.выражение вектороного произведения через координаты сомножителя.
если
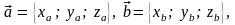 то
то
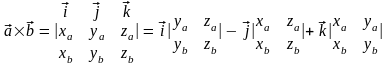
59.Угол между векторами. условие коллинеарностии ортогональности.
) Угол между векторами:
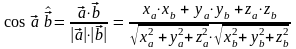 ;
;
2) Условие ортогональности (перпендикулярности) ненулевых векторов:
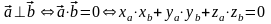
3) Условие коллинеарности:
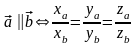
60.Смешанное произведение векторов, определение свойств, геометрический смысл.
Смешанное
произведение векторов: определение,
свойства, геометрический смысл.
Смешанным произведением
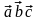 трех векторов
трех векторов
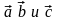 называется
скалярное произведение вектора
называется
скалярное произведение вектора
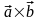 и вектора
и вектора
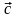 .
По определению
.
По определению
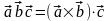 Свойства
смешанного произведения:
Свойства
смешанного произведения:
1)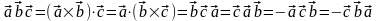
2)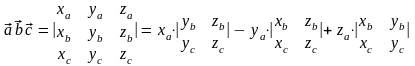
3)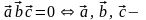 компланарны.
компланарны.
Геометрический смысл: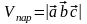 ,
,
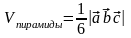
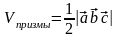
61.Выражение смешенного произведения через координаты сомножителей.
Если
векторы
 заданы своими координатами
заданы своими координатами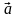 =
{
=
{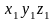 }
}
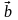 ={
={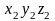 }
}
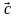 ={
={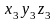 }
, то смешанное произведение
определяется формулой
=
}
, то смешанное произведение
определяется формулой
=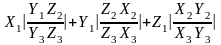 Доказательство:
имеем
=
(
x
)
x
=
Доказательство:
имеем
=
(
x
)
x
=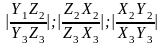 Умножая скалярно
=
{
Умножая скалярно
=
{ }
на вектор
x
получаем:
=
}
на вектор
x
получаем:
=
62.Приложение векторов к решению задач. деление отрезка в данном отношении, расстояние между точками,вычисление площади треугольника,работысилы,объема параллелепипеда.
Расстояние
между точками:
если даны две точки плоскости
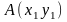 и
и
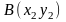 то расстояние между ними (отрезок АВ)
равно:
то расстояние между ними (отрезок АВ)
равно:
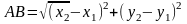 А
если в пространстве
А
если в пространстве
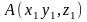 и
и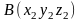
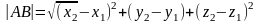 .Деление
отрезка заданного отношения: если
известны две точки плоскости
.Деление
отрезка заданного отношения: если
известны две точки плоскости
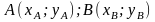 то координаты точки М
то координаты точки М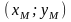 ,
которая делит отрезок АВ в отношении
,
которая делит отрезок АВ в отношении
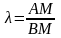 выражаются формулами:
выражаются формулами:
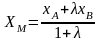
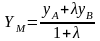 .Вычисление
площади треугольника:
.Вычисление
площади треугольника:
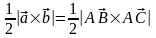 (основание
на боковую сторону).
Объём параллелепипеда:
(основание
на боковую сторону).
Объём параллелепипеда: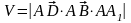 Работа
силы:
Работа
силы:
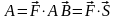 ,где
,где
 -
вектор силы
-
вектор силы
 - перемещение
- перемещение
