48.Решение систем линейных алгебраических уравнений по правилу Крамера.

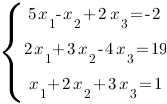Решение: Составим и вычислим сначала главный определитель этой системы: 

Так как  , то система имеет единственное решение, которое можно найти по правилу Крамера: где   получаются из определителя   путем замены 1-го, 2-го или 3-го столбца, соответственно, на столбец свободных членов. Таким образом: Итак,   - единственное решение.

МатричныйметодЗапишем систему (1) в виде где  Решение: Построим обратную матрицу  . Вычислим алгебраические дополнения ко всем элементам, причём алгебраические дополнения, вычисленные для элементов первой строки, записываются первым столбцом матрицы .Знак   определяется как  : т.е.   имеет вид: .Примечания: 1. При умножении матрицы на число все элементы матрицы умножаются на это число2. Умножение матриц возможно, если число столбцов первого сомножителя равно числу строк второго сомножителя.3. При умножении матриц элемент матрицы произведения равен сумме произведений элементов строки 1-го сомножителя матрицы на соответствующие элементы столбца 2-го сомножителя матрицы.Находим матрицу-решение: .Таким образом,  .

49.Ранг матрицы.Решение уравнений методом Гаусса.

50.Понятие Векторных функций скалярного аргумента их непрерывность.

Задание вектор-функции скалярного аргумента означает задание трех скалярных функций A_i(t),i=x,y,z . В этом случае говорят, что вектор-функция задана в декартовой системе координат. (Здесь и далее предполагается, что в сокращенной записи с использованием индексных обозначений e₁=i , e₂=j ,e₂=k и соответственно A_x=A₁ ,A_y=A₂ ,A_z=A₃ , а также используется правило Дифференцирование вектор-функции двух скалярных аргументов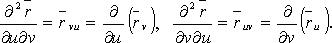 

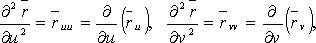
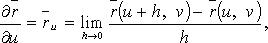
51.Векторы на плоскости и в пространстве и линейные операции над ними.

Вектор – это направленный отрезок прямой.То есть, в качестве вектора мы принимаем отрезок на плоскости или в пространстве, считая одну из его граничных точек началом, другую – концом.Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скалярПримеры:

Дано:

Сложение:

Умножение:

Умножение вектора на число:

52.Линейные зависимости и независемость вектаров.Базис.

Линейная зависимость и независимость векторов

Набор векторов   называется системой векторов. Система из   векторов   называется линейно зависимой, если существуют такие числа  , не все равные нулю одновременно, что Система из   векторов   называется линейно независимой, если равенство возможно только при  , т.е. когда линейная комбинация в левой части равенства тривиальная. 1. Один вектор   тоже образует систему: при   — линейно зависимую, а при   — линейно независимую. 2. Любая часть системы векторов называется подсистемой. Базисом в трехмерном пространстве R3 называется упорядоченная тройка любых линейно-независимых векторов.

Базис R².и R³

d={α,β}=[ α ]εR^2

[β]

d={α,β ,γ}=[ α ]εR^3

[β]

[γ]

Разложение произвольного вектора по базису. Каждый вектор на плоскости может единым образом представлен в линейной комбинации базисных векторов на этой плоскости(этого пространства).Коэффициент этой линейной комбинации называется координатой вектора в данном базисе. Замечание. 2 коллинеарные векторы зависимы. 3 коллинеарные векторы в пространстве также линейно зависимы если векторы не коллинеарные, то они образуют базис на плоскости, а не коллинеарные базис в пространстве.