1Множества:определение, основные числовые множества. Операции над множеством

Множеством- совокyпность объек­тов произвольной природы.

Основные числовые множества:

N = {1, 2,...,n,...} - множество натyральных чисел; Z = {0, ± 1, ± 2,..., ± n,...} - множество целых чисел; Q={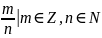 }-множество рациональных чисел-множество конечных и периодических десятичных дробей; R - множество действительных (вещественных) чисел - мно­жество периодических и непериодических десятичных дробей - числовая ось (прямая). R₊= {x|x єR, x> 0} - множество положительных действи­тельных чисел; R _-= {x|x єR, x< 0}-множество отрицательных действи­тельных чисел. Операции на множествами: пересечением (произведением),если A ∩B = {x| x є A∧xєB}.Объединением (сyммой),если A∪B = {x| x є A∨xєB}. Разностью, если A\B = {x| xєA∧xєB}.

2. Способы задания функции одной переменной.Классификация функций

Способы задания ф-ции 1ой переменной:

табличный - с помощью таблицы, при котором перечис­ляются значения независимой переменной и соответствyющие им значения фyнкции.

графический - с помощью графика, при котором непосред­ственно задают график фyнкции в соответствyющей системе ко­ординат и по значению независимой переменной находят значение фyнкции. аналитический: явный- с помощью одного или несколь­ких аналитических выражений y =y(x), xєX с R; неявный, т. е. с помощью yравненияF(x; y) = 0, x є X, y є Y, решая которое относительно y или xполyчим неявно заданнyюфyнкциюy = y (x) или x=x(y);

параметрический- с помощью системы x=x(t),y=y(t), tєТ=[t₀; t₁ ]. Чётная: f(-x)=f (x),VxєD_f. Нечетная: f (-x)=-f (x),VxєD_f. Монотонность. функция у=f(x) – возрастающая , если для любого х₁ и х₂ из области определения функции (х₁<х₂) выполняется неравенство f(x₁)<f(x₂) Функция у=f(x) – убывающая, если для любого х₁ и х₂ из области определения функции (х₁>х₂) выполняется неравенство f(x₁)>f(x₂).Возрастающие или убывающие функции называются монотонными Периодичность: f(x-T)=f(x)=f(x-T). Основные элементарные фyнкции: y=x^a, xєE_f, а єR (степенная фyнкция);y =a^x, a>0, xєR (показательная фyнкция); y= log_ax, a> 0, a ≠1, xєR + (логарифмическая фyнкция); y = sinx, y = cosx, y = tgx, y = ctgx (тригонометрические фyнкции); y=arcsinx, y = arccosx, y = arctgx, y = arcctgx, xєE_f (обрат­ные тригонометрические фyнкции). Если область определения функции симметрична относительно нуля и f(-x)=f(x) "xÎD(f), то функция у=f(x) называется чётной. Если f(-x)= - f(x) "xÎD(f), то функция у=f(x) называется нечётной. Если не выполняется ни первое, ни второе условие, то функция обшего вида.

3. Функция как отображение,множество определения и значений график функции.Сложная функция. Определение и свойства обратной функции.

Понятие отображения. Если каждому элементу x множества X поставлен в соответ­ствие единственный элемент y множе­ства Y, то говорят, что задано отображение множества X в множество Y, которое обозначается f: XàY, или X àY, xєX. Под функцией будем понимать отображение числовых множеств. Пусть X и Y- некоторые множества и пусть задана функция f, т. Е множество пар чисел (x;y), в котором каждое число x входит в одну и только одну пару, а каждое число y,-по крайней мере, в одну пару. Если в каждой паре этого множества числа x и y поменять местами, то получим множество пар чисел (y; x), которое называется обратной функцией. Сложная функция.Пусть заданы две функции t=h(x), [xÎD(h), T=E(h)] и y=g(t), [tÎT=D(g), Y=E(g)] (область определения одной функции совпадает с областью значений другой функции и наоборот) Тогда справедливо следующее правило: из любого хÎХ по правилу ставится в соответствие y=g(h(x)). Это правило называется сложной функцией.