Министерство образования и науки Украины
Севастопольский государственный технический университет
ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В
СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
С ПОМОЩЬЮ ВЕЩЕСТВЕННЫХ ЧАСТОТНЫХ
ХАРАКТЕРИСТИК
Методические указания к выполнению лабораторной работы по дисциплине «Теория автоматического управления»
Севастополь
2001
СОДЕРЖАНИЕ
Стр.
1 Цель работы 2
2 Краткие теоретические сведения 2
3 Описание технических средств выполнения работы 5
4 Порядок выполнения теоретических расчетов 5
5 Порядок выполнения экспериментальных исследований 5
6 Содержание отчета о выполнении лабораторной работы 6
7 Контрольные вопросы 6
Библиография 7
1 Цель работы
Применение метода трапеций к исследованию переходных процессов в линейных системах автоматического управления (ЛСАУ).
2 Краткие теоретические сведения
При решении различного рода задач управления всегда возникает необходимость исследования переходных процессов, протекающих в ЛСАУ.
Устойчивость является необходимым, но недостаточным условием работоспособности САУ. Устойчивость системы управления означает лишь то, что в системе происходит затухание переходного процесса под влиянием управляющего или возмущающего внешнего воздействия. Время затухания процесса, максимальное отклонение регулируемой величины и число колебаний в системе при этом не определяются, однако эти величины являются очень важными показателями качества процессов регулирования.
Показатели качества процессов регулирования можно определить с помощью различных методов. К числу их в первую очередь следует отнести построение переходных процессов по заданным передаточным функциям замкнутых систем [1]. Существует несколько методов построения переходных процессов в САУ [1,2], однако все они имеют свои определенные достоинства и недостатки, а также границы применимости.
В
данной лабораторной работе решается
задача построения переходного процесса
в ЛСАУ методом трапецеидальных частотных
характеристик
[1,2].
Метод
приближенного построения кривой
переходного процесса в ЛСАУ по заданной
вещественной частотной характеристике
(ВЧХ) Р(
замкнутой системы был разработан В.В.
Солодовниковым в 1948 году. Этот способ
полезен тогда, когда расчет системы
ведется с самого начала частотными
методами. Он совершенно необходим, если
известны уравнения не всех звеньев
системы, а часть из них задается
экспериментально снятыми частотными
характеристиками.
Частотный метод построения переходных процессов заключается в графическом способе вычисления интеграла
,
t>0.
Представим
кривую P
в виде
суммы ряда типовых трапецеидальных
кривых p
(
(рис. 1):
P()
;
(1)
тогда
,
(2)
т.е.
.
(3)
0
Рисунок 1 – Произвольная трапецеидальная частотная
характеристика
Будем
считать, что функция
определяется с помощью следующего
выражения:
(4)
Функция и представляет собой трапецеидальную частотную характеристику. Подставив выражение (4) в формулу (2), получим
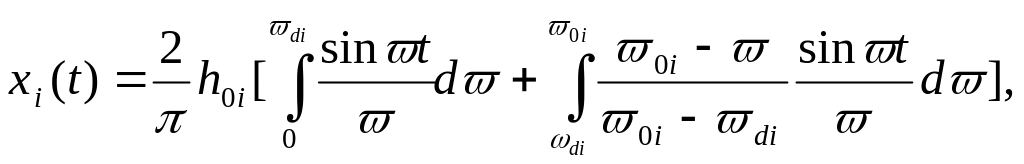(5)
откуда после ряда несложных преобразований найдем
(6)
где
Si(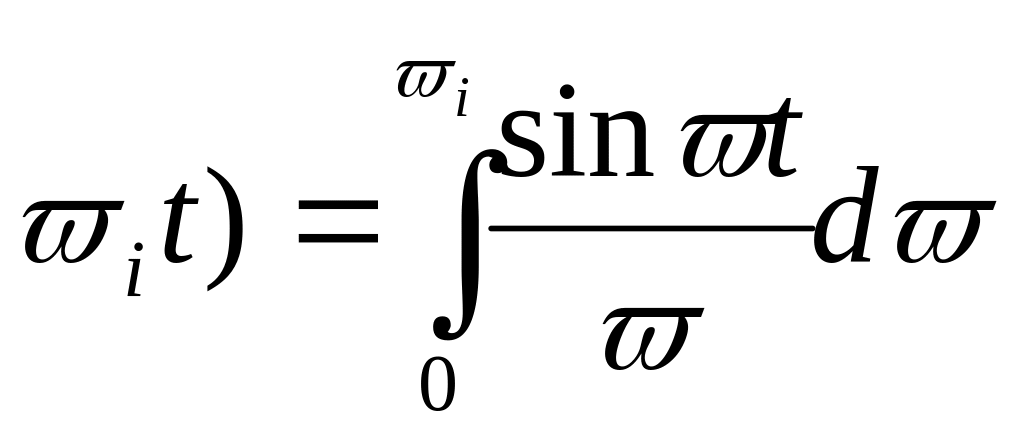
.
Для
составления таблиц функции x
(t)
В.В.
Солодовников предложил использовать
единичные трапецеидальные частотные
характеристики, имеющие h
=1,
=1
и коэффициент ,
изменяющийся в пределах от 0 до 1,0
(рис.2). Пользуясь этими характеристиками,
переходную функцию в соответствии с
формулой (6) можно представить в виде
,
(7)
откуда
видно, что функции h
зависят только от одного параметра ,
и их можно представить в виде таблиц. С
помощью этих таблиц можно вычислять
переходные процессы в системах
регулирования с точностью 2-5%.
p
1
0 1
Рисунок 2 – Единичная трапецеидальная частотная
характеристика
Порядок построения переходного процесса по частотной характеристике замкнутой системы следующий:
Разбиваем ВЧХ на n трапеций. Определяем для каждой из трапеций
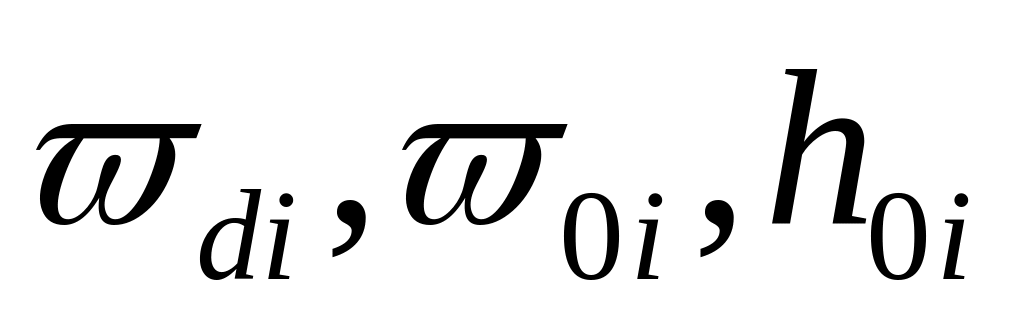.Вычисляем для каждой из трапеций наклон
.
По вычисленному
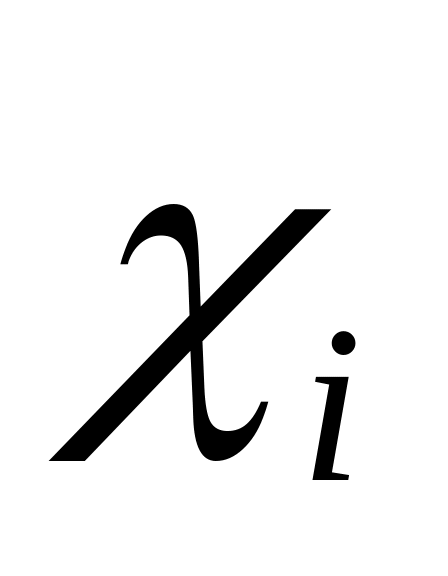находим по таблице соответствующие
значения
-функций
при
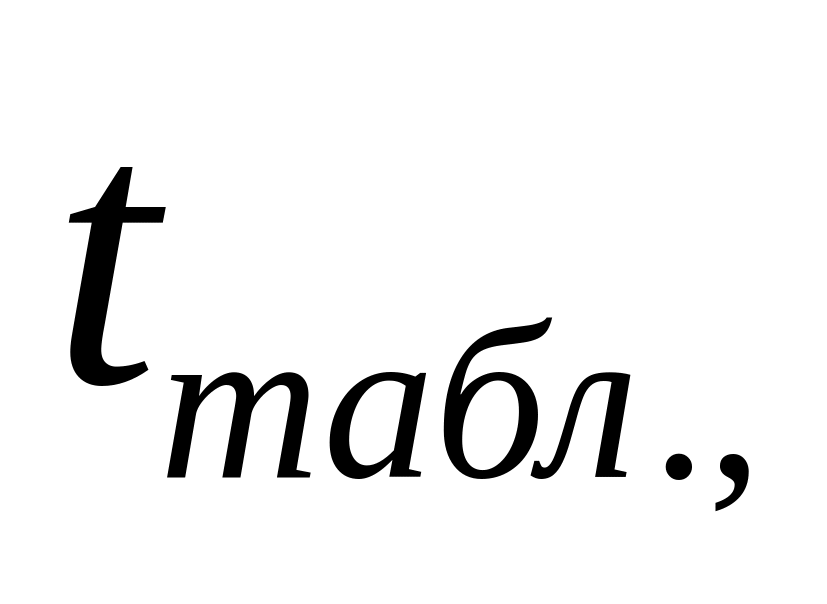
Полученные значения умножаем на высоты трапеций .
Откладывая по оси t значения t
,
а по оси ординат значения
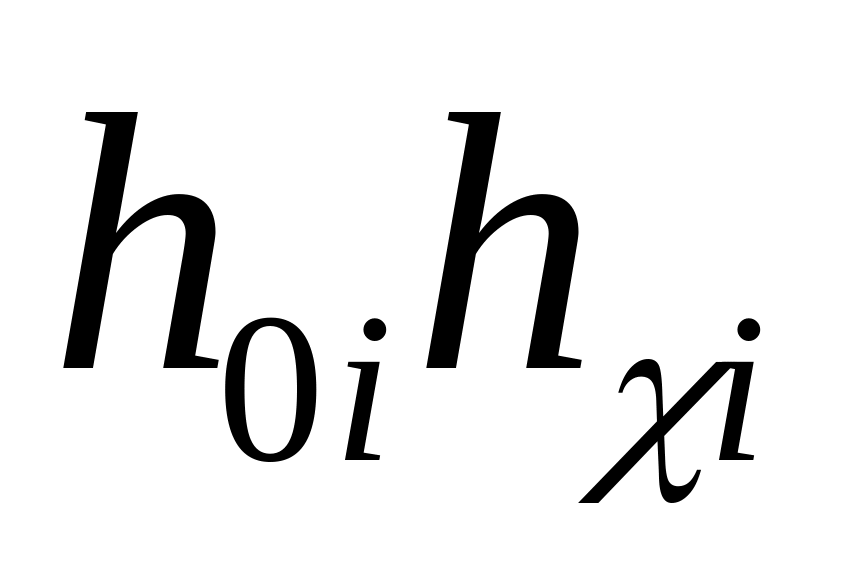получим составляющие переходных
процессов
x
(t)
для каждой из трапеций.Складывая ординаты этих кривых с учетом их знака, получим искомый переходный процесс x(t).