I. Организационный момент.

II. Лабораторная графифеская работа «Функция, обратная данной».

Цель работы: закрепить понятие обратной функции.

Оборудование: карточки с заданием, миллиметровая бумага, масштабные линейки, цветные карандаши, комбинированные лекала.

Х о д р а б о т ы

Задание пишется на доске:

1) Отношение f задано с помощью пар:

а)

б) .

1. Изобразите данное отношение f с помощью стрелок.

2. Является ли данное отношение f функцией?

3. Задайте с помощью пар обратное отношение g.

4. В одной и той же системе координат построить график данного отношения f (одним цветом) и обратного отношения g (другим цветом).

5. Является ли данное отношение g функцией?

2) Найдите функцию, обратную данной:

а) f , если х ;

б) g , если х ;

Постройте графики функций f и g , а так же обратных им функций (разным цветом). Как расположены их графики относительно прямой у=х?

Учащимся раздаются конверты или папки, в которых лежат два цветных карандаша разного цвета, линейка, комбинированные лекала, миллиметровая бумага, карточка с заданием. Карточки можно заготовить по вариантам или по количеству учащихся.

ОБРАЗЕЦ КАРТОЧКИ

1. а)

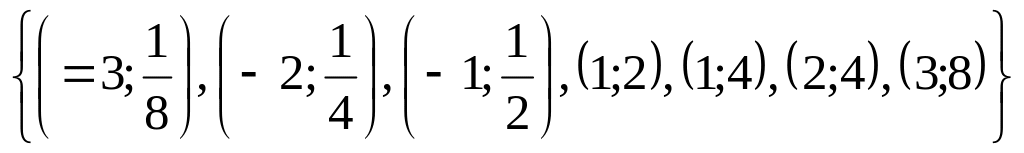
б)

2. а) f(х)= , где х .

б) g(х)= , где х .

III. Изучение нового материала.

1. Уравнения называются равносильными, если они имеют одно и то же множество корней, а так же если они не имеют корней.

2. Если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.

№139(1, 3, 5) – по очереди на доске.

Ответ: 1)да, 3)нет, 5)нет.

№141 – под диктовку.

Ответ: 1)второе, 2)второе.

Сделать вывод, при каких преобразованиях исходное уравнение заменяется на равносильное ему уравнение. (Если некоторое выражение в левой или правой части уравнения заменить тождественно равным ему выражением.).

Например, №141(2): левую и правую части первого уравнения умножили на выражение х-1, получили второе уравнение. Данное преобразование не является тождественным. Корень х=1 второго уравнения не является корнем первого уравнения. Его называют посторонним корнем. Преобразуем первое уравнение следующим образом:

х-2=0

х=2 – корень данного уравнения.

Выполним такие же преобразования по следующим уравнением:

х -3х+2=х-1

(х-1)(х-2)=х-1

х-2=1

х=3.

Но исходное уравнение имеет два корня. Проверьте самостоятельно, найдите второй корень. Подумайте, почему произошла потеря корня.

Итак, при решении уравнений можно делать только такие его преобразования, при которых не происходит потери корней. Если при этом получается уравнение – следствие данного, то необходима проверка найденных корней, так как возможно появление посторонних корней.

Решить уравнение: №138(4), №142(1, 3), №147.

Ответ: №138(4) нет корней;

№142(1) х =0; х ; (3) х =5; х =6.

№147 х=3.

IV. Домашнее задание: №138(2, 3), №139(2, 4, 6), №142(2, 4).

6. Итог урока.

7. Дополнительное задание.

№150 – дается индивидуально.

Решение.

1.

х или х-3=1

х х=4

Ответ: х

2.

х или х

х х х -х-2=0

х=2 или х=-1

Ответ: х х , х =2.

3.

х -4=-3х или х+3=1 или х+3=0

х +3х-4=0 х=-2 если

х=-4 или х=1 х=-3

Ответ: х =-4, х =1, х =-2, х =-3.

4.

х или х+3=1 или х+3=0, если

х х=-2

х=3 или х=-1 х=-3 не подходит.

Ответ: х

У р о к 13