
- •Практическая часть.
- •Организационный момент.
- •Теоретическая часть.
- •Организационный момент.
- •Актуализация опорных знаний.
- •Теоретическая часть.
- •Организационный момент.
- •Проверка знаний (5-7 мин).
- •I. Организационный момент.
- •II. Теоретическая часть.
- •III. Практическая часть.
- •Дополнительное задание.
- •I. Организационный момент.
- •II. Проверка знаний (5 мин.).
- •III. Решение заданий.
- •Организационный момент.
- •Организационный момент.
- •Итоги и анализ зачетной работы.
- •Теоретическая часть.
- •Практическая часть.
- •Итог урока.
- •Организационный момент.
- •Решение заданий.
- •Итог урока.
- •Итог урока.
- •Организационный момент.
- •Актуализация опорных знаний.
- •Теоретическая часть.
- •I. Организационный момент.
- •II. Лабораторная графифеская работа «Функция, обратная данной».
- •III. Изучение нового материала.
- •I. Организационный момент.
- •II. Проверка знаний.
- •I. Организационный момент.
- •II. Актуализация опорных знаний.
- •III. Изучение нового материала.
- •V. Итог урока.
- •VI. Дополнительное задание.
- •I. Организационный момент.
- •II. Решение уравнений.
- •IV. Итог урока.
- •I. Организационный момент.
- •II. Самостоятельная работа.
Домашнее задание: №125(2, 4, 6, 8), №175(2, 6), №179(1,3).
Итог урока.
ДИКТАНТ
Укажите область определения функции у=х
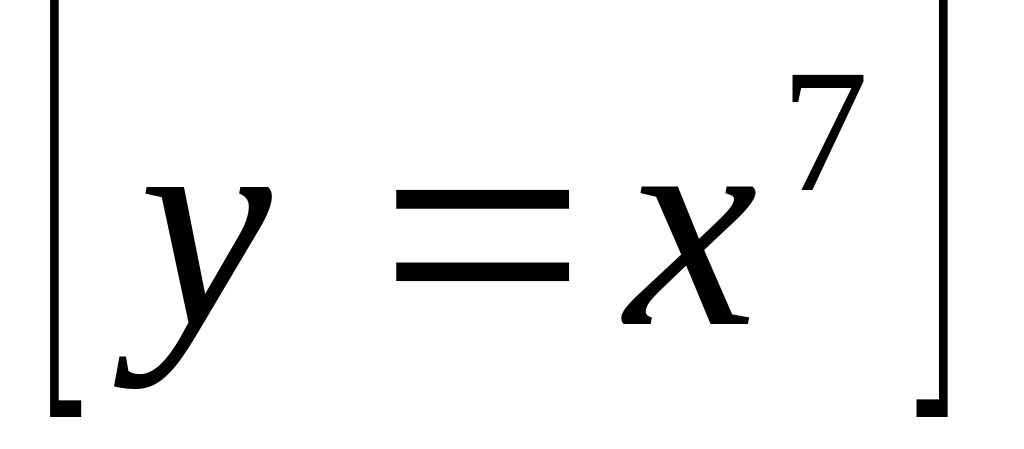 .
.Укажите множество значений функции у=х
 .
.Является ли функция у=х
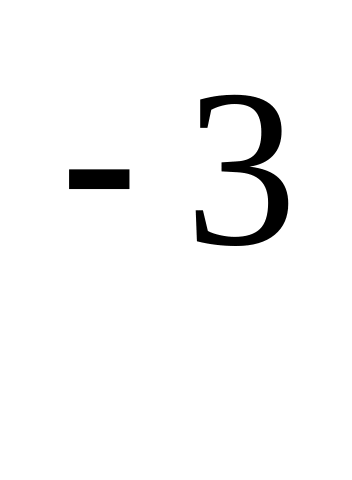
 возрастающей?
возрастающей?Изобразите схематически график функции у=х
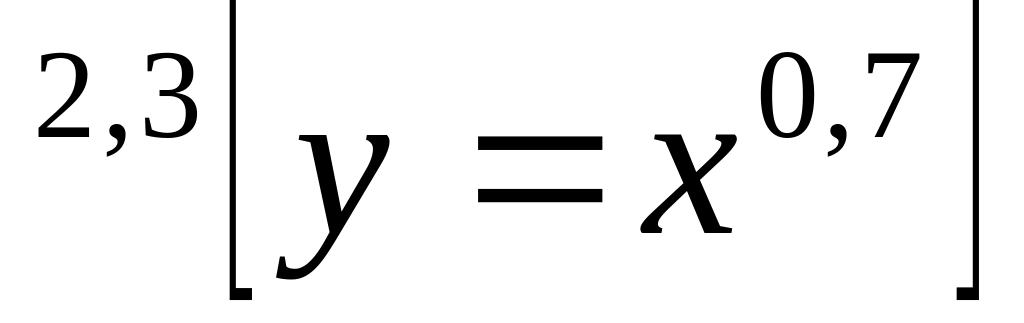 .
.Найдите область определения функции у=
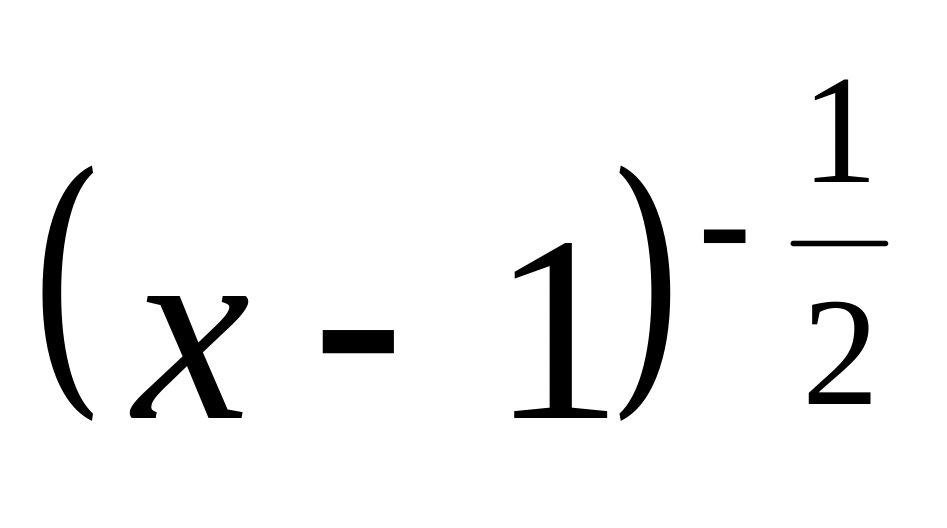
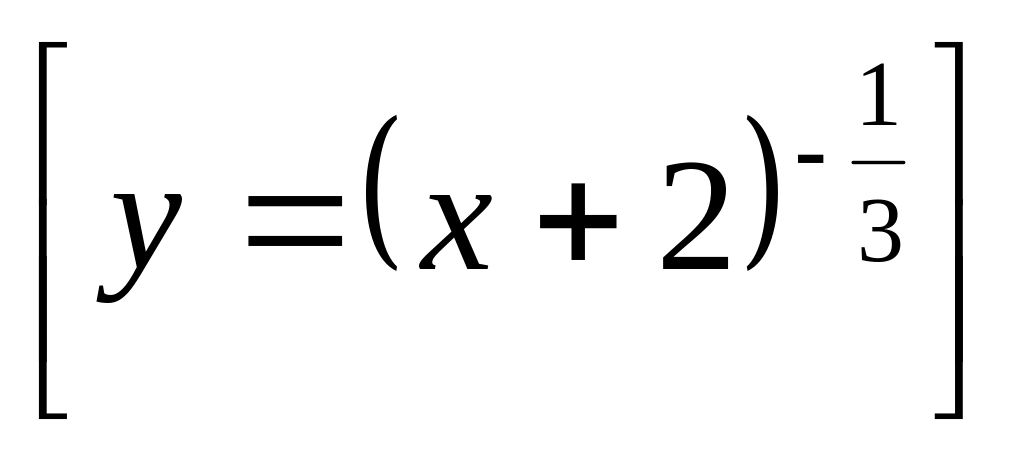 .
.Сравните число 5,2
 с единицей.
с единицей.Сравните
 и
и
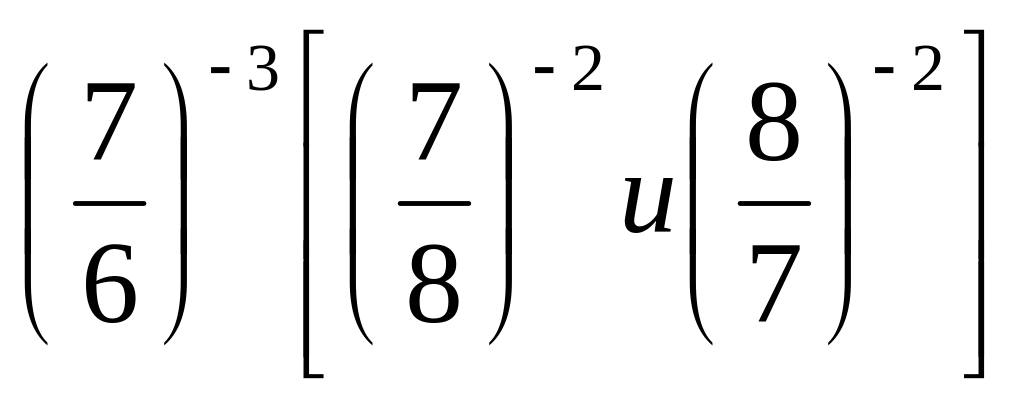 .
.В одной системе координат постройте графики функций у=х и у=х
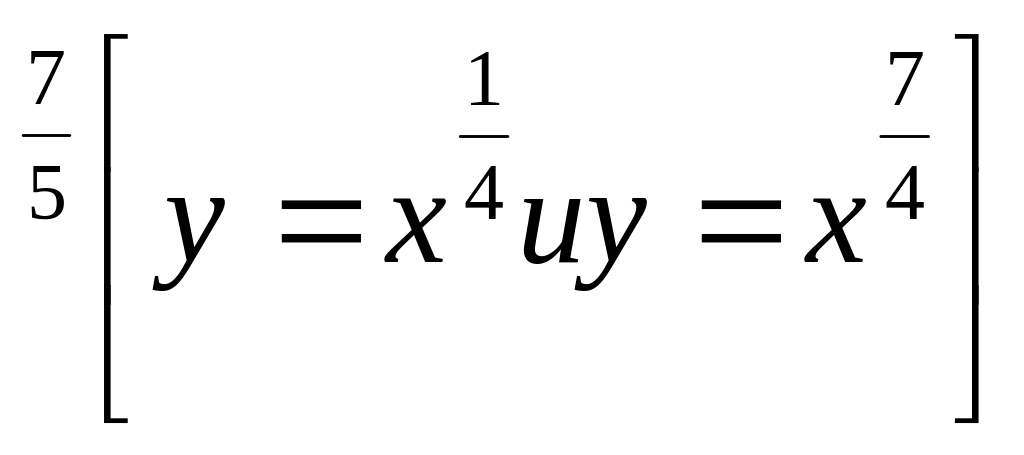 .
.Решите уравнение х
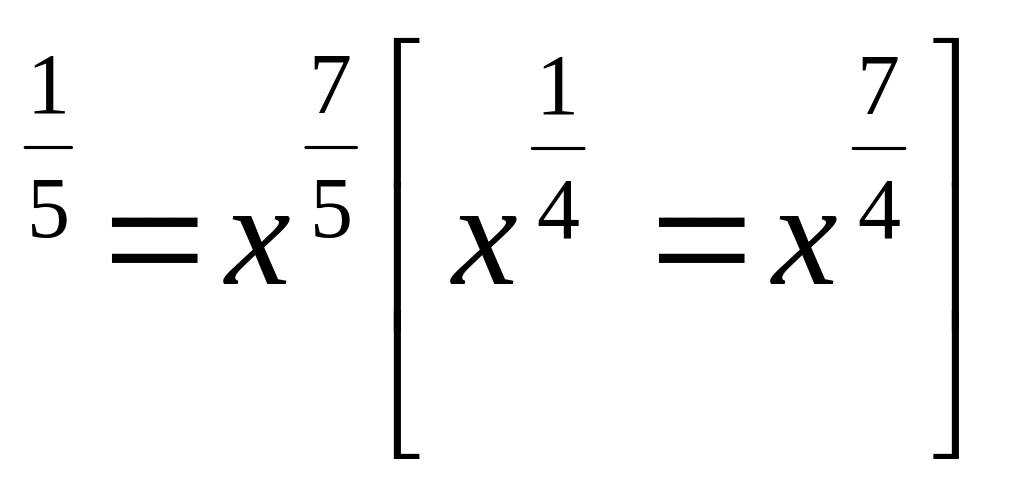 .
.Решите неравенство х
 .
.
Итог урока.
ВЗАИМООБРАЗНЫЕ ФУНКЦИИ
ЗНАНИЯ И НАВЫКИ УЧАЩИХСЯ
Знать определение функции обратной для данной функции, теоремы об обратной функции; уметь строить график функции, обратной данной.
Урок 11
Организационный момент.
Актуализация опорных знаний.
Выразить:
Переменную r из
формулы S=![]() ;
;
а Р=2(а+b);
v
a=![]() ;
;
А
N=![]() ;
;
b
![]() .
.
2. Как построить фигуру, симметричную относительно некоторой прямой?
Перечертите по клеточкам рисунки и выполните осевую симметрию.
Укажите промежутки возрастания (убывания) функций:
У=5х+2;
У=х![]() ;
;
У=![]() ;
;
У=х ;
У=7х .
Теоретическая часть.
Ввести понятия:
«монотонная функция» (возрастающая (убывающая) функция); «обратимая функция» (функция, которая принимает каждое свое значение только при одном значении х);
«взаимно обратные
функции» (если обратимая функция у=![]() задана формулой, то для нахождения
обратной функции нужно решить уравнение
=у
относительно х и затем поменять местами
х и у. Если у=
является обратной к найденной для нее
обратной у=g(x),
то эти функции взаимно обратны).
задана формулой, то для нахождения
обратной функции нужно решить уравнение
=у
относительно х и затем поменять местами
х и у. Если у=
является обратной к найденной для нее
обратной у=g(x),
то эти функции взаимно обратны).
Доказать теорему 1 и теорему 2.
Практическая часть.
№131 – устно.
Ответ: 1)да, 2)нет, 3)да, 4)да, 5)нет, 6)да.
№132(1, 3, 5) – на доске по очереди.
Ответ: 1)у=![]() ,
3)у=3х+2, 5)у=
,
3)у=3х+2, 5)у=![]() .
.
№133 (1, 3, 5, 6) – под диктовку.
Ответ: 1) Д(у)=R, Е(у)=R;
2) Д(у)=R, Е(у)=R;
5) х ; у ;
6) х
;
у![]() .
.
№134(в, г) – самостоятельно по вариантам.
№135 – устно, с рассуждением.
Ответ: 1)да, 2)нет, 3)да, 4)да.
Домашнее задание: №132(2, 4, 6), №133(2, 4), №136(2, 3).
Итог урока. Объясните, что такое монотонная функция, обратимая функция, взаимно обратные функции. Приведите примеры.
Дополнительное задание.
№137 – работа в группах (8 групп).
Решение.
у=3х-1 и у=

Д(у)=R Е(у)=R
Е(у)=R Е(у)=R
у=
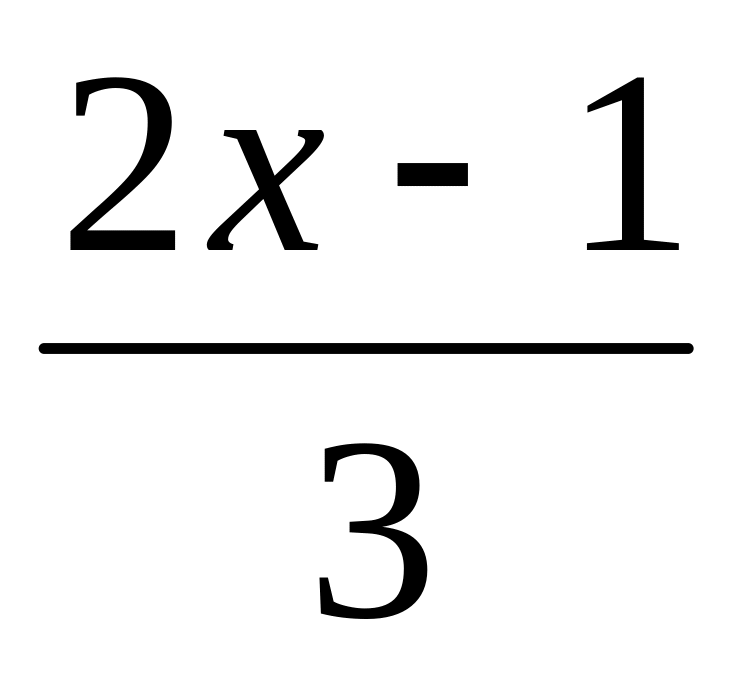 и
у=
и
у=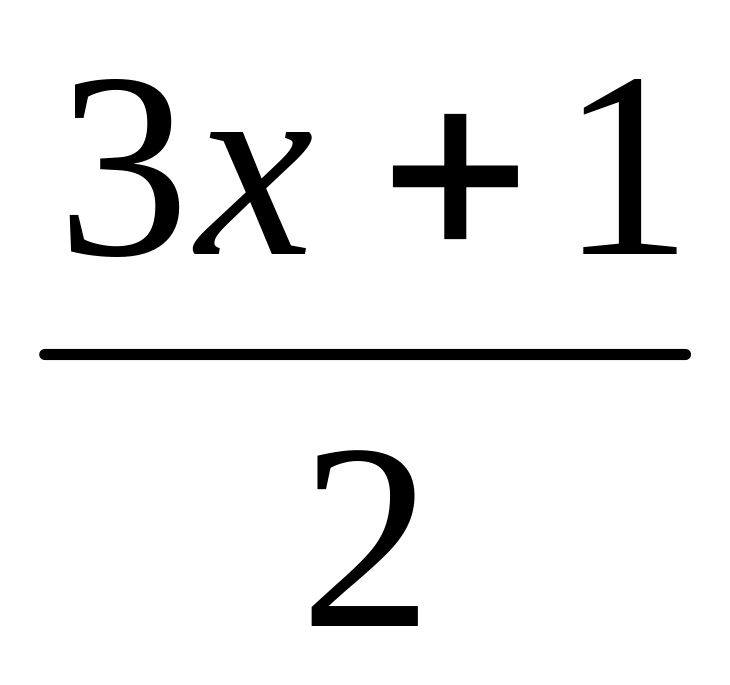
Д(у)=R Д(у)=R
Е(у)=R Е(у)=R
у=х -1, х и у=
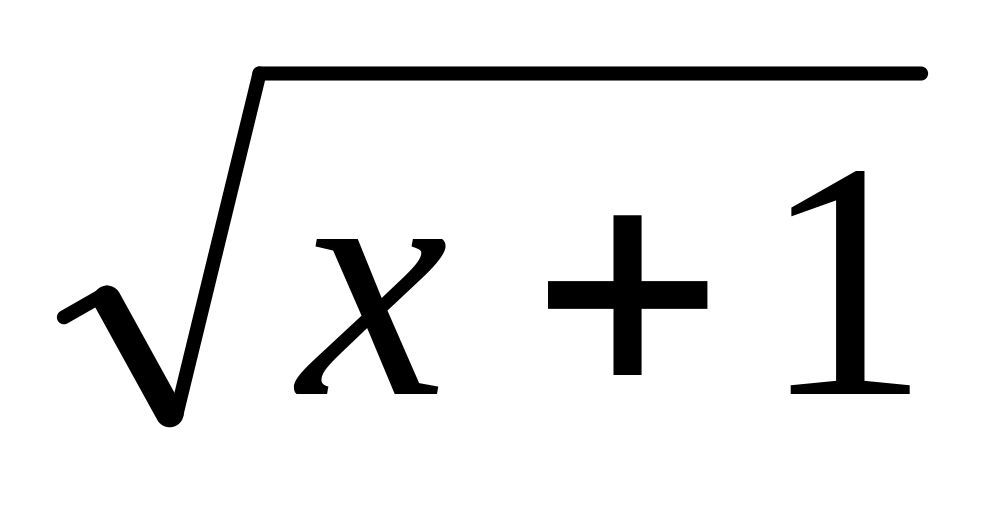
Д(у)=![]() Д(у)=
Д(у)=![]()
Е(у)= Е(у)=
у=
 ,
х
и
у=
,
х
и
у=
Д(у)=![]() Д(у)=
Д(у)=
Е(у)= Е(у)=
у=х -2 и у=
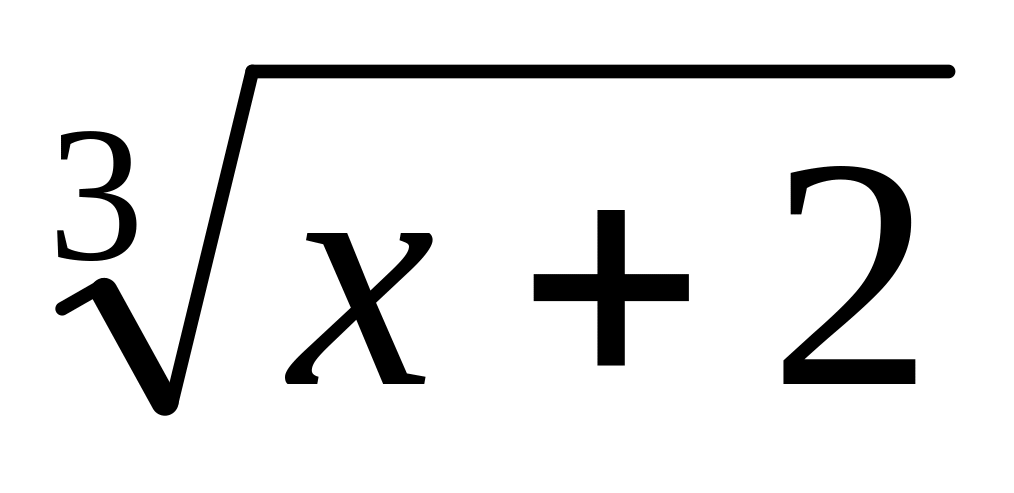
Д(у)=R Д(у)=R
Е(у)=R Е(у)=R
6. у=![]() и у=
и у=![]()
Д(у)=R Д(у)=R
Е(у)=R Е(у)=R
7.у=![]() и у=х
и у=х![]() ,
х
,
х
Д(у)= Д(у)=
Е(у)= Е(у)=
8. у=
и у=![]() ,
х
,
х
Д(у)= Д(у)=
Е(у)= Е(у)=
РАВНОСИЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
ЗНАНИЯ И НАВЫКИ УЧАЩИХСЯ
Знать определение равносильных уравнений, следствия уравнения; знать, при каких преобразованиях исходное уравнение заменяется на равносильное ему уравнение, при каких получаются посторонние корни, при каких происходит потеря корней; знать определение равносильных неравенств; уметь устанавливать равносильность и следствие, уметь выполнять необходимые преобразования при решении уравнений и неравенств.
У р о к
