I. Организационный момент.
II. Теоретическая часть.
Ввести определение степени с рациональным показателем а
=
,
где m
z,
а>0.Показать, что все свойства степени с натуральным показателем верны для степени с любым рациональным показателем и положительным основанием. Эти свойства получаются из свойств корней.
Ввести определение степени с действительным показателем а
.
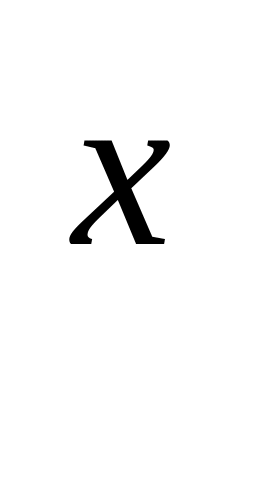Для нее сохраняются все известные
свойства степени с рациональным
показателем:
1).
.
2).
.
3)
.
4)
.
5)
,
кроме того:
6)
>1
при a>1,
x>0.
4. Рассмотреть теорему и три следствия из нее. Они помогают при решении уравнений и неравенств, сравнении чисел. Запишем их следующим образом:
1. Пусть а>0, а
,
а
=а
.
Тогда х
.
2. Пусть х
и а
.
Тогда а
;
0<a<1,
a
>a
.
Пусть 0<x
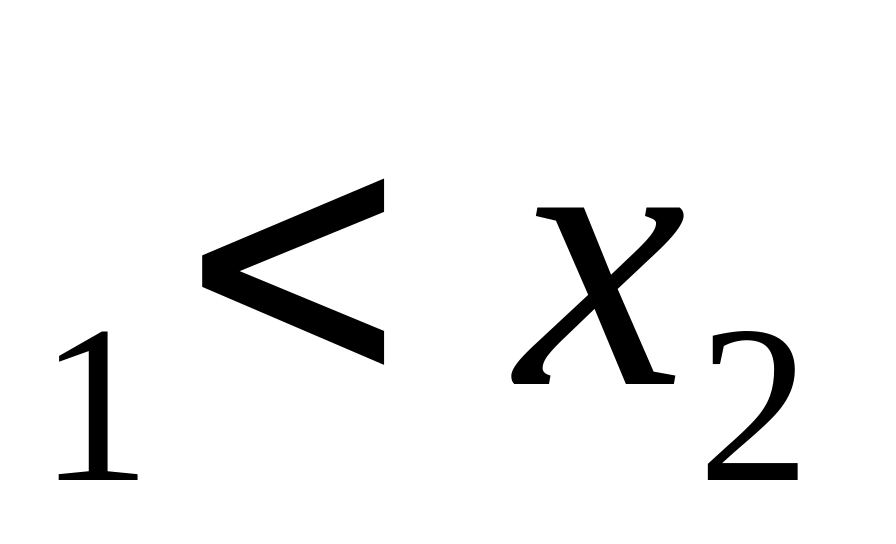и р>0. Тогда х
;
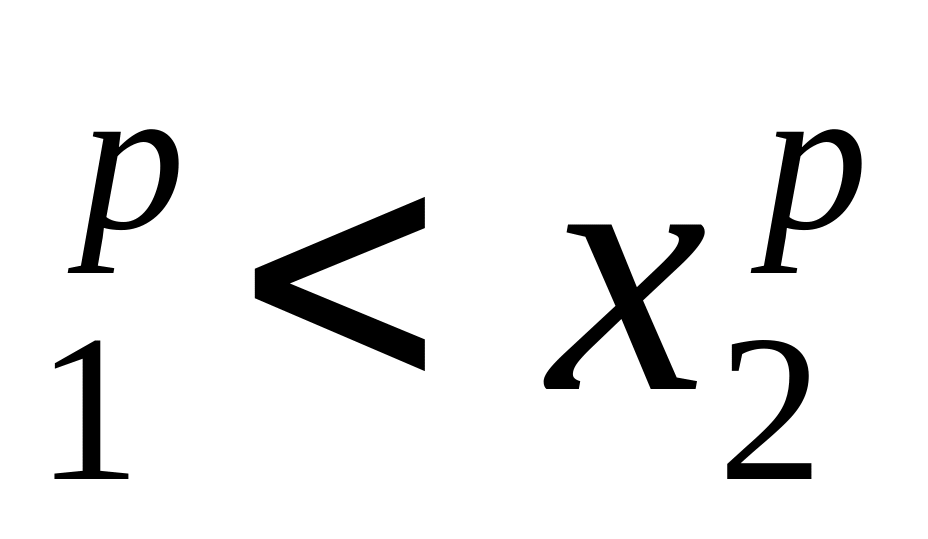p<0,
x
.
III. Практическая часть.
№55, №56 – устно по очереди.
Ответ: №55 1) х
; 2) а
;
3) b
;
4) х
;
5) а
;
6) b
.
№56 1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
№60 (1) – учитель с классом.
Решение.
.
№60(2) – самостоятельно.
№60(3) – на доске.
№60(4) – под диктовку.
Ответ: 2) 121; 3)-1; 4)150.
На доске по очереди выполняются номера: №69(1, 4), №70(3), №71(1, 3).
Ответ: №69 (1) 4; (4)
-
;
№70(3) 3;
№71(1) 5; (3)
.
№76 – работа в парах с взаимопроверкой. Первые парты выполняют первый пример, вторые – второй и т.д. Ученики, сидящие за одной партой, выполнив задание, обмениваются тетрадями. Устно проверяются ответы.
Ответ: 1)36,5; 2)5
;
3)9
;
4)10
.
Пусть х . Если а>1, то а <а .
Если
0<a<1, то а
Пользуясь этими свойствами, устно выполнить №72.
№84 – под диктовку.
Ответ: 1)х=2; 2)х=-
; 3)х=
;
4)х=2
.
№85(1) – учитель с классом.
№85(3) – на доске по желаню.
Ответ: 1) -
;
3)х=3.
IV. Домашнее задание: №69(2); №70(2, 4); №71(2, 4); №79, №85(2, 4).
V. Итог урока. Что нового узнали на уроке? (В виде беседы с классом)
Дополнительное задание.
№90, 91 – дается индивидуально.
№90. Решение по формуле сложных процентов:
S=а
находим
S=5000
.
Ответ: 5306 р. 4 к.
№91. Решение.
2 гоода 7 месяцев=2
года.
По формуле сложных процентов находим
S=2000
.
Ответ: 2158 р. 70 к.
У р о к
I. Организационный момент.
II. Проверка знаний (5 мин.).
ТЕСТ
Найдите область определения функции у=
.
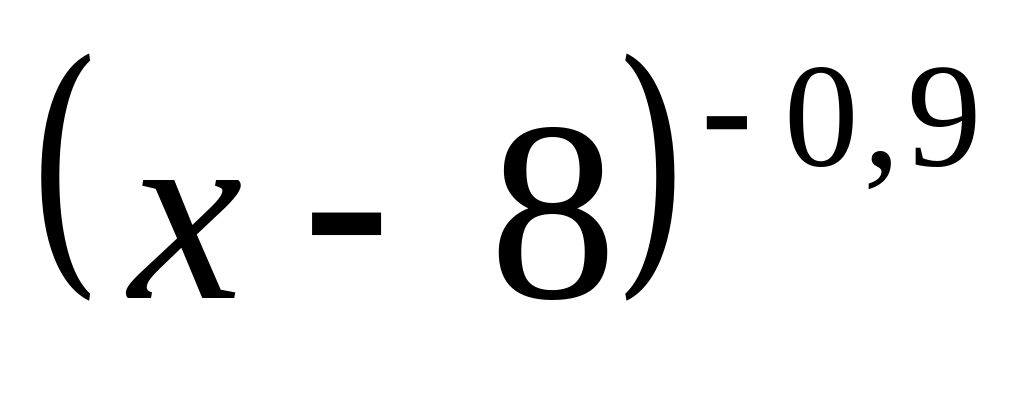А. х – любое число;
Б. х
;
В. х>8; Г. х<8.
2. Вычислите
.
А.1; Б.3
;
В.3; Г.3
.
3. Решите уравнение
4
.
А.
;
Б.
;
В.
;
Г.
.
4. Сравните числа
.
А.
;
Б.
;
В.
;
Г. нельзя сравнить.
5. Запишите числа
27
;
;
81
в порядке возрастания.
А. ; 81 ; 27 .
Б.81
;
27
;
.
В.27 ; 81 ; .
Г. ; 27 ; 81 .
Ответ: В А В В А.
III. Решение заданий.
Используя свойства степени с рациональным показателем выполнять следующие задания на доске по очереди:
№61(1,3,5), №77, №80(1,3), №82(1).
Ответы: №61(1) а
;
(3) b
;
(5) х
.
№77(1)
;
(2) а
.
№80(1) а
;
(3)
.
№82(1)
.
Дифференцированное задание.
Уровень I (более слабый): №63, 64, 65.
Уровень II: №66, 67.
Уровень III: №78, 81.
Уровень IV: №87(1, 3), 89.
Учащиеся работают самостоятельно. Решение всех заданий демонстрируется на доске (с №63 до №89).
IV. Домашнее задание: №1-5 “Проверь себя» на с.37. Подготовиться к зачету по главе I. Выполнить тренажер №1 (см. Приложение).
Итог урока. Результаты теста. Анализ ошибок.
У р о к
Цель: проверить знания, умения и навыки учащихся по теме «Действительные числа».