Организационный момент.
Актуализация опорных знаний.
Вычислить (устно):
8
;
(-1)
;
-2
;
;
5
;
(-5)
;
0
;
(-3)
;
(0,3)
;
(0,2)
;
7
;
7
;
10
;
.
Решить уравнение:
А) х -4=0; б) х =8; в) х - 81=0.
Теоретическая часть.
Арифметическим
корнем натуральной степени n
2
из неотрицательного числа а
называется неотрицательное число, n-я
степень которого равна а.
=в
в
=а,
где а
,
в
.
Свойства арифметического корня n-й степени:
1)
=
;
3)
=
;
2)
=
;
4)
=
,
где а
,
в>0, m
2,
n
2,
m
N,
n
N.
5)
=
,
k
N;
6)
=
.
Практическая часть.
№27 – устно по очереди.
Ответ: 1)1; 0; 4; 0,9;
13;
.
2)1; 0; 5;
;
0,3; 0,4.
3) 0; 1; 2;
;
;
0,2.
№28, 29 – устно по очереди, используя свойство 6).
Ответ: №28: 1)6; 2)2;
3)
;
4)15.
Ответ №29: 1)100; 2)81;
3)
;
4)
.
№32 (1; 3; 5) – на доске по очереди.
Ответ: 1)-4
;
3)4; 5)
.
Выполняем №33-36 (1, 3) под диктовку по очереди, применяя различные свойства арифметического корня.
Ответ: №33 1)3,5; 3)20;
№34 1)35; 3)1,6;
№35 1)10; 3)6;
№36 1)72; 3)3.
№42, 43 (1, 3) – самостоятельно. Во время выполнения задания учитель проходит по классу, отмечает различные способы решения. Затем просит нескольких учащихся записать свое решение на доске.
Например: №42 (1):
=
=7
или
=
=7.
Ответ: 1)2
;
2)6; 3)3; 4)
;
5)4; 6)4.
Домашнее задание. №32(2, 4, 6). №42 (2, 4), №43 (2, 4), №50.
Итог урока. Вопросы по теории:
Что такое арифметический корень натуральной степени?
Какие свойства корня вы знаете?
Дополнительное задание. №53.
(Дается индивидуально.)
Решение.
1)
-
=2
-
=2
-
=2
-
=2
1+ - +1=2
2=2 верно
2)
+
=3
+
=3
Возведем в куб
сумму 3+
:
=27+27
+45+5
=72+32
=8(9+4
).
+
=3
+
=3
+
=3;
+
=3;
3=3 верно.
У р о к
Организационный момент.
Проверка знаний (5-7 мин).
П Р О В Е Р О Ч Н А Я Р А Б О ТА
Вариант I
Найдите значение выражения:
а)
;
б)
;
в)
.
2. Вычислите:
а)
;
б)
.
3. Вычислите:
.
Вариант II.
Найдите значение выражения:
а)
;
б)
;
в)
.
2. Вычислите:
а)
;
б)
.
3. Вычислите:
.
Ответ: В-I: 1)а)78; б)20; в)2,16; 2) а)2; б) 36; 3)3.
В-II: 1) а)54; б)18; в)2,16; 2) а)2; б) 72; 3)3.
Решение задач.
Перечислить свойства арифметического корня натуральной степени (опросить несколько учащихся).
По очереди на доске выполняются номера: №38(1, 3), №41(1, 3), №44(1, 3, 4, 5).
Ответы: №38 (1) 2ав; (3) а;
№41 (1) ав;
(3)
;
№44 (1) х
;
(3) а
в
;
(4) а
в
;
(5) а
в.
Вспомнить область допустимых значений выражения.
Выражение имеет смысл при любых значениях переменной, кроме следующих случаев:
- если имеется рациональная дробь (в этом случае знаменатель не равен нулю);
- если имеется арифметический корень четной степени (в этом случае покоренное выражение неотрицательно);
- если имеется тангенс или котангенс;
- если имеется логарифм.
Последние два случая мы рассмотрим позднее.
Выполнить №45 (3, 4).
При решении №45(3) вспомнить метод параболы, №45(4) – метод интервалов.
Ответ: 3)х
-
;
х
;
4)
х
2.
№49 (1) – учитель показывает решение на доске:
+
=
+
=а
+
=а
+а
=2а
.
№49 (3) – по диктовку.
№49 (4) – за доской.
Ответ: 1) 2а ; 3) 0; 4) а-1.
Разобрать задачу 6 в тексте параграфа, затем выполнить №51 (2, 3,4) самостоятельно по вариантам. Класс делится на три варианта; проверка выполняется устно.
Ответ: 2) (3-х) при х 3, (х-3) при х>3; 3) 9; 4)-3х-5.
Домашнее задание: №38(4); №41(2); №44(6); №48(1); №49(2).
Итог урока.
Дополнительное задание. №54.
Выполняется в группах.
Решение:
1.
=
-
=
.
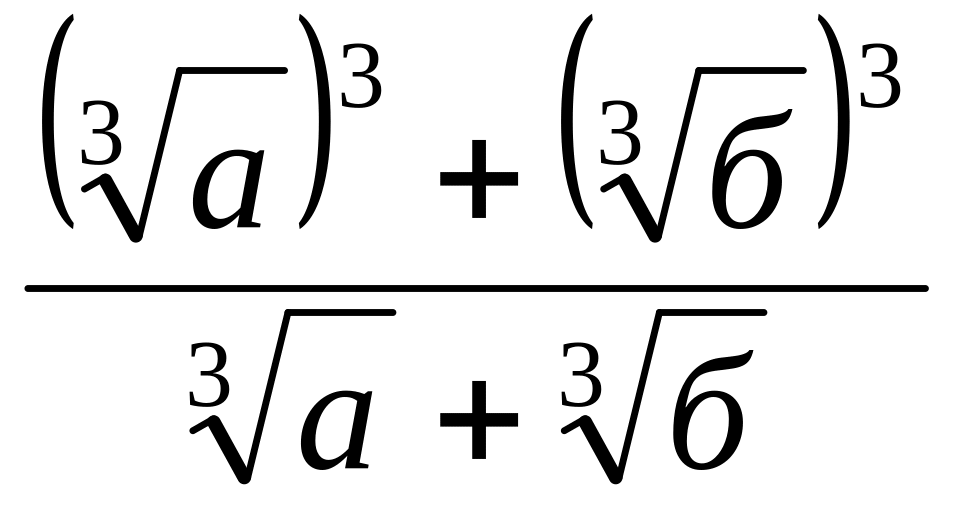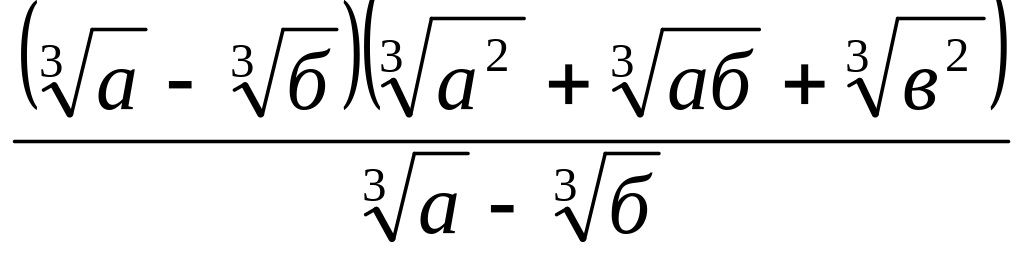2.
-
=
-
=
-
=
=2
.
3.
=
=
=
.
СТЕПЕНЬ С РАЦИАОНАЛЬНЫМ И
ДЕЙСТВИТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
ЗНАНИЯ И НАВЫКИ УЧАЩИХСЯ.
Знать определение степени с рациональным показателем, свойства этой степени; определение степени с действительным показателем, теорему и три следствия из нее; уметь выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем.