Целые и рациональные числа

Знания и навыки учащихся

Знать, что такое натуральное, целое, рациональное число, периодическая дробь; уметь записывать бесконечную десятичную дробь в виде обыкновенной, уметь выполнять действия с десятичными и обыкновенными дробями.

1. Организационный момент.

2. Теоретическая часть.

1. Первоначально под числом понимали лишь натуральные числа, которых достаточно для счета отдельных предметов. Множество N= 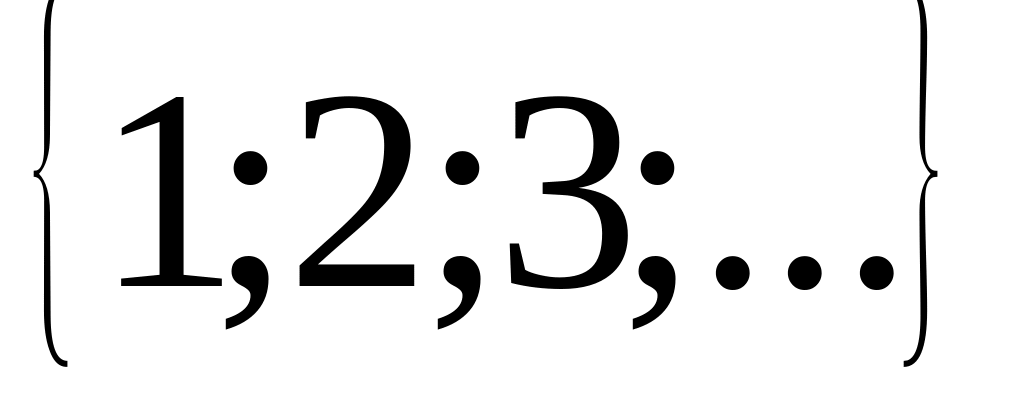натуральных чисел замкнуто относительно операций сложения и умножения. Это значит, что сумма и произведение натуральных чисел являются числами натуральными.

2. Однако разность двух натуральных чисел уже не всегда является натуральным числом. Приведите примеры. (5-5=0; 5-7=-2, числа 0 и -2 не являются натуральными). Так результат вычитания двух одинаковых натуральных чисел приводит к понятию нуля и введению множества целых неотрицательных чисел Z 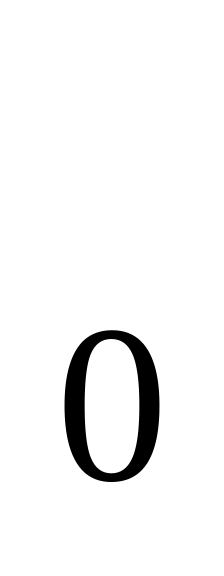= 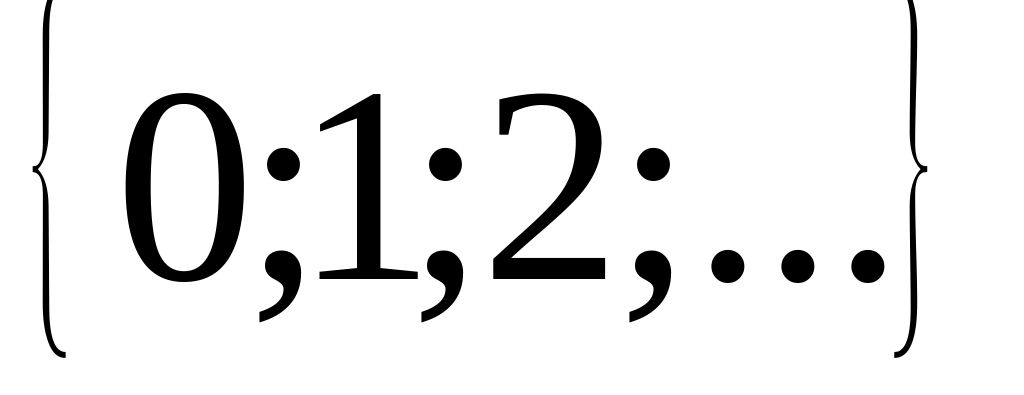. Чтобы сделать выполнимой операцию вычитания, вводят отрицательные целые числа, то есть числа, противоположные натуральным. Таким образом получают множество целых чисел. Z= .

3. Чтобы сделать выполнимой операцию деления на любое число, не равное нулю, необходимо к множеству всех целых чисел присоединить множество всех положительных и отрицательных дробей. В результате получается множество рациональных чисел. Q= 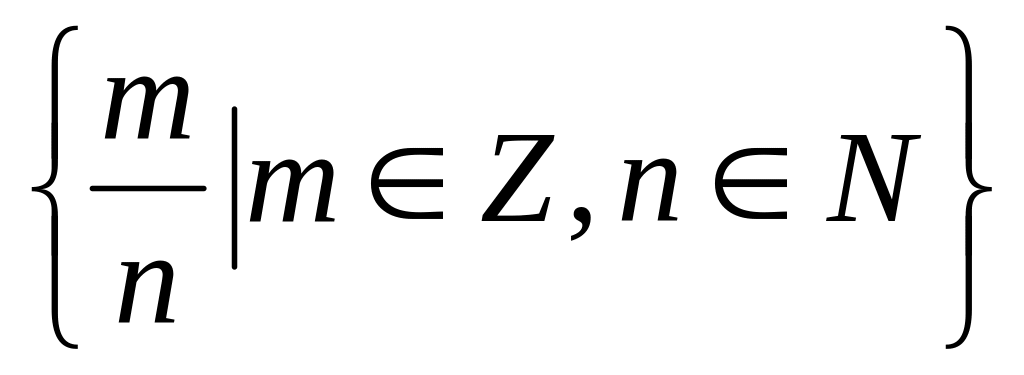. При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.

4. Каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби. Вспомним, что такое периодическая дробь. Это бесконечная десятичная дробь , у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби. Например, 0,3333….=0,(3) 1,057373…=1,05(73). Читаются эти дроби так: «0 целых и 3 в периоде», «1 целая, 5 сотых и 73 в периоде». Запишем рациональные числа в виде бесконечной периодической десятичной дроби: натуральное число 25 = 25,00…= 25,(0); целое число -7=-7,00…=-7,(0); обыкновенная дробь - 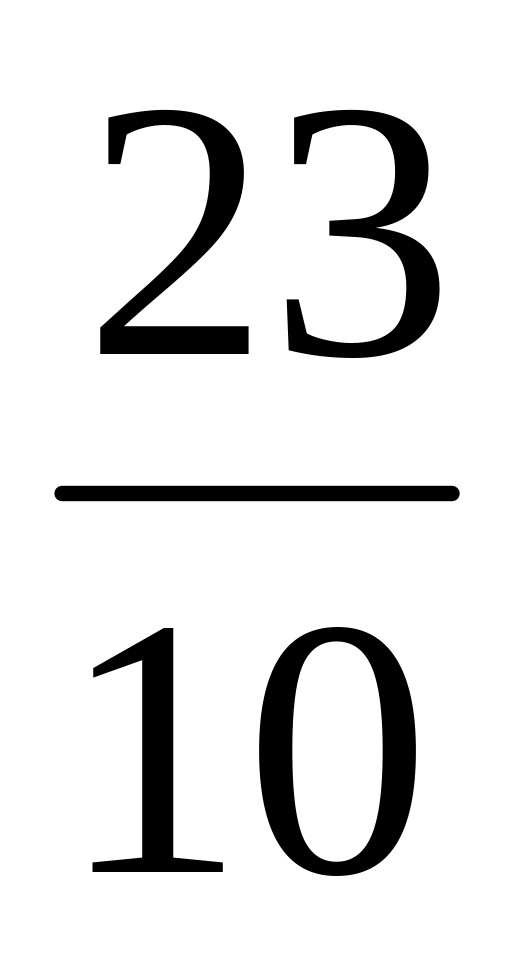=-2,300…=-2,3(0); =1,533…=1,5(3). Воспользуемся алгоритмом деления уголком.

5. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби , где m – целое число, n – натуральное число. Рассмотрим в качестве примера задачу 2 из параграфа учебника и составим алгоритм.

1) Пусть х=0,2(18) Умножая Нужно умножить дробь на 10 , где

на 10, получаем 10х=2,1818… n- количество десятичных знаков,

содержащихся в записи этой дроби

до периода: х .

2) Умножая обе части послед- Умножаем на 10 , где k- количество

него равенства на 100, находим цифр в периоде.

1000х=218,1818… х = х .

3) Вычитая из равенства (2) Отнимем от равенства (2) равенство

равенство (1), получаем 990х (1), решим полученное уравнение.

=216.

Отсюда х= .

3. Практическая часть.

№1(1) – на доске.

№1(3) – под диктовку. (Все учащиеся выполняют задание в тетрадях, один ученик проговаривает вслух решение.)

№1(5) – самостоятельно. (Учащиеся выполняют задания в тетрадях. Выполнив задание ученик поднимает руку. Дождавшись, когда весь класс или его большая часть справится с заданием, проверяем решение. Либо учитель опрашивает несколько учеников, либо один ученик сообщает ответ и выясняем, нет ли другого ответа, либо учитель сам сообщает верный ответ. Желательно использовать сигнальные карточки – карточки с одной стороны зеленого цвета, с другой – красного. Каждый ученик имеет такую карточку, если он согласен с прозвучавшим ответом, то показывает учителю зеленую сторону карточки, если не согласен – красную.)

Ответ: 1) 0,(6); №3 0,6; 5)-8,(285714).

№2(1) – на доске.

№2(3) – за доской.(Учащиеся выполняют задание в тетрадях. Один ученик записывает решение а откидной доске или «за доской», затем открывает доску и комментирует свое решение.)

№2(5) – под диктовку.

Ответ: 1)0,(29); 3)1,58(3); 5)0,225.

№3(6) – учитель показывает на доске решение, опираясь на алгоритм.

Х=-2,3(82)=-2,3828282…

10х=-23,828282…

1000х=-2382,8282…

1000х-10х=-2382,8282…-(-23,828282…)

990х=-2359

Х=- .

№3 (1,3,5) – на доске по очереди. (Учащиеся выходят к доске по очереди, начиная с ученика, сидящего на первом варианте первой парты у окна. Обычно учащиеся запоминают, кто отвечал у доски последним и кто должен пойти к доске после него при выполнении следующего задания с такой формой работы.)

Ответ: 1) ; 3) ; 5)-3 .

№4 - самостоятельно по вариантам. (Учащиеся, сидящие на первом варианте, выполняют первый пример, на втором варианте – второй. Справившись с заданием, ученик поднимает руку. Затем работаем с сигнальными карточками – см. №1(5).)

Ответ: 1)4; 2)4,75.

№5(1) – на отметку. (Ориентируясь на уровень подготовки класса, учитель либо вызывает одного ученика к доске и затем ставит ему отметку за решение, либо учащиеся самостоятельно выполняют задание и отметку получает ученик, первым правильно решивший пример.)

Ответ: 8,5.

4. Домашнее задание: №1(2,4,6,0, №2(2,4,6), №3(2,4), №5(2).

5. Итог урока: по вопросам.

1. Множество каких чисел вы знаете? (Натуральные, целые, рациональные). Приведите примеры.

2. Что такое периодическая дробь? Как записать ее в виде обыкновенной?

Действительные числа

Знания и навыки учащихся

Иметь понятие об иррациональных числах, множестве действительных чисел, одуле действительного числа; уметь выполнять с иррациональными выражениями, сравнивать числовые значения иррациональных выражений.

1. Организационный момент.

В организационный момент включается проверка домашнего задания, если это не будет оговорено особо. В классе выбираются или назначаются три консультанта (по одному с каждого ряда), которые проверяют наличие домашней работы и в начале урока сообщают результаты проверки работы учителю. Затем учитель выясняет, какие задания вызвали затруднения, какие вопросы возникли и учеников. Если затруднения испытали один-два ученика, то подключаются к работе консультанты (во внеурочное время). Если большинство учащихся класса не справились с каким-либо заданием, то это задание следует разобрать в классе.