
|
ЛАБОРАТОРНАЯ РАБОТА. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО МАЯТНИКОВ |
|
Цель работы.
И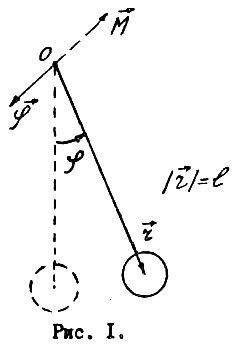 зучение
колебательных движений маятников.
Измерение ускорения свободного падения.
зучение
колебательных движений маятников.
Измерение ускорения свободного падения.
Оборудование.
Универсальный маятник fpm-04
Темы для изучения.
В лабораторной работе рассмотрены основные понятия и законы, на которых основан принцип действия математического и оборотного маятников, получена рабочая формула для определения ускорения силы тяжести при помощи математического и оборотного маятников, проведено описание экспериментальной установки и порядка работы на ней.
Лабораторная работа предназначена для студентов, выполняющих общий физический практикум в лаборатории механики кафедры экспериментальной физики ТГУ.
Краткая теория.
У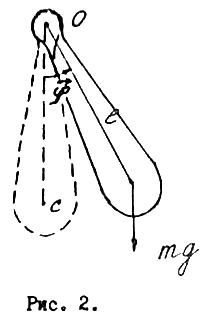 скорение
свободного падения относительно Земли
в разных точках земного шара различно.
Это обусловлено неинерциальностью
системы отсчета, связанной с Землей, и
изменением силы гравитационного
взаимодействия рассматриваемого
тела с Землей в различных ее точках.
скорение
свободного падения относительно Земли
в разных точках земного шара различно.
Это обусловлено неинерциальностью
системы отсчета, связанной с Землей, и
изменением силы гравитационного
взаимодействия рассматриваемого
тела с Землей в различных ее точках.
Поэтому измерение ускорения свободного падения в различных точках Земли с одной стороны дает указания о форме Земли, а с другой стороны позволяет обнаруживать различные местные неоднородности в строении земного шара.
Одним из методов достаточно точного определения ускорения свободного падения является исследование колебательного движения маятников.
В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебательное движение относительно неподвижной оси. Различают математический и физический маятники.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити (рис.1).
Физическим маятником называют твердое тело, закрепленное на горизонтальной оси, проходящей через точку О расположенную выше его центра тяжести С (рис. 2).
Рассмотрим динамику движения этих маятников.
При отклонении маятников
на угол ![]() из
из
положения равновесия
возникает вращательный момент ![]() относительно точки О.
В данном случае на тело действуют
только моменты силы тяжести, так как
момент силы реакции оси равен нулю.
Известно, что сумма моментов сил тяжести
равна моменту равнодействующей силы
относительно точки О.
В данном случае на тело действуют
только моменты силы тяжести, так как
момент силы реакции оси равен нулю.
Известно, что сумма моментов сил тяжести
равна моменту равнодействующей силы
![]() ,
при условии, что она приложена к
центру тяжести, В однородном поле центр
тяжести совпадает с центром масс
тела.
,
при условии, что она приложена к
центру тяжести, В однородном поле центр
тяжести совпадает с центром масс
тела.
По определению момент
силы ![]() относительно
точки O:
относительно
точки O:
![]() ,
где
,
где ![]() - радиус-вектор точки приложены силы
относительно точки О.
- радиус-вектор точки приложены силы
относительно точки О.
Уравнением движения тела, закрепленного на неподвижной оси, является основное уравнение динамики вращательного движения, имеющее вид:
![]() (1)
(1)
где ℐ
- момент инерции тела
относительно оси; ![]() - угловое ускорение. .
- угловое ускорение. .
Под вектором угла
понимается вектор, по модулю равный
![]() и направленный вдоль оси вращения таким
образом, чтобы с его начала
и направленный вдоль оси вращения таким
образом, чтобы с его начала
|
ЛАБОРАТОРНАЯ РАБОТА. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ ПОМОЩИ МАТЕМАТИЧЕСКОГО И ОБОРОТНОГО МАЯТНИКОВ |
|
поворот наблюдался происходящим по часовой стрелке.
По определению векторного произведения момент силы тяжести будет в данном случае направлен противоположно направлению .
Для решения дифференциального
уравнения (1) перейдем от векторной
формы к скалярной. Рассмотрим проекции
векторов
и
на ось координат,
совпадающую с осью вращения и направленную
по ![]()
Составляющая момента силы
![]() относительно
точки О
вдоль оси, проходящей
через эту точку, называется моментом
силы относительно оси.
относительно
точки О
вдоль оси, проходящей
через эту точку, называется моментом
силы относительно оси.
Вектор![]() можно
записать следующим образом:
можно
записать следующим образом:
![]() ,
где
,
где![]() -
единичный вектор, направленный вдоль
,
а
-
единичный вектор, направленный вдоль
,
а ![]() ,
тогда угловое ускорение
,
тогда угловое ускорение ![]() ,
так как направление вектора
не меняется со временем.
,
так как направление вектора
не меняется со временем.
Таким образом, уравнение (1) в проекции на выбранную координатную ось запишется:
![]() (2)
(2)
Поскольку ![]() ,
где
,
где ![]() .
Знак
(-), как
уже говорилось, учитывает то обстоятельство,
что
направлен противоположно
. •
.
Знак
(-), как
уже говорилось, учитывает то обстоятельство,
что
направлен противоположно
. •
Если ограничиться случаем
малых отклонений из положения равновесия,
то можно считать ![]() .
.
Уравнение (2) при этом переходит в уравнение:
![]() (3)
(3)
и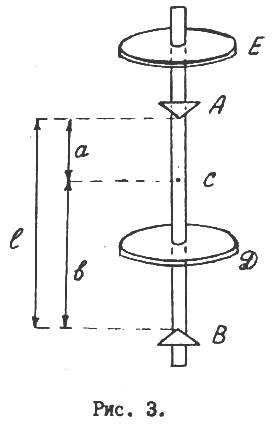 ли
ли
![]() (4)
(4)
Поделив обе части уравнения (4) на ℐ, подучим уравнение, описывающее гармонические колебания:
![]() (5)
(5)
Общим решением уравнения (5) будет функция вида:
![]() (6) (б)
(6) (б)
где A и ∝ - произвольные постоянные, определяемые на начальных условий, a
![]() -
циклическая частота колебаний.
-
циклическая частота колебаний.
Поскольку период колебаний
и циклическая частота связаны
соотношением ![]() можем определить период рассматриваемых
гармонических колебаний:
можем определить период рассматриваемых
гармонических колебаний:
![]() (7)
(7)
Из (7) получаем непосредственно выражение для ускорения свободного падения
![]() (8)
(8)
Таким образом, зная период
колебаний маятника и его момент инерции»
можно определить ускорение свободного
падения. Для математического маятника
момент инерции ![]() .
.
Следовательно, ускорение свободного падения при помощи колебаний математического маятника можно определить по формуле:
![]() (9)
(9)
Формула (9) является формулой для расчета ускорения свободного падения при колебаниях математического маятника.
Для физического маятника появляются трудности с определением момента инерции ℐ, который трудно вычислить с большой степенью точности. Поэтому для измерения g описанным способом используются маятники особой конструкции, которые позволяют либо легко вычислять момент инерция, либо исключить его из рассмотрения.
В данной работе используется так называемый оборотный маятник, конструкция которого позволяет исключить момент инерции на рассмотрения.

