4. Результаты работы

1.

2.

dy(x,C1) =

y(x,C1,C2) =

3. Характеристическое уравнение:

Корни характеристического уравнения: k₁ = k₂ =

Общее решение уравнения:

Поверка правильности решения: (запись с экрана)

4.

v(t,C1) =

C1 =

S(t,C1,C2) =

C2 =

S(t,C1,C2) =

5.

given

___________________ = ________________

y( ) = ____

y := odesolve (x,___ , _____)

x:= ____ , ______ .. ____

x = y(x)=

6.

y:=

F(x,y):=

y1:=rkfixced(y,___ , ____ , ____, F

y1=

7.

given

___________________ = ________________

y( ) = ____

y := odesolve (x,___ , _____)

x:= ____ , ______ .. ____

x = y(x)=

h(x):=

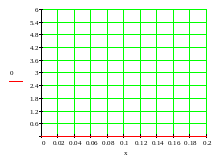
5. Вывод

В ходе выполнения данной работы _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ПРАКТИЧЕСКАЯ РАБОТА 9

Числовые и степенные ряды.

1. Цель работы

1.1 Научиться вычислять члены числового ряда и исследовать числовые ряды на сходимость

1. Научиться раскладывать функции в ряды Тейлора и Маклорена

2. Ход работы:

2.1 Вариант

1. Найдите первые три члена ряда : .

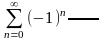2. Определить сходится или расходится данный геометрический ряд :

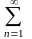
3. Определить сходится или расходится данный гармонический ряд :

4. Выполняется ли необходимый признак сходимости у ряда :

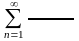
5. С помощью предельного признака исследовать ряд :

6. С помощью признака Даламбера исследовать сходимость ряда : .

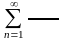7. С помощью признака Коши исследовать сходимость ряда :

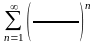
8. Исследовать на сходимость знакочередующийся ряд. Если ряд сходятся, то определить, сходятся он абсолютно или условно.

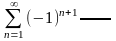
9. Разложите многочлен по степеням .

10. Написать первые три, отличные от нуля, члена разложения по степеням х функции

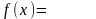
11. Разложите функции в степенной ряд используя разложение элементарных функций и определите интервал сходимости:

1.