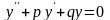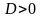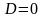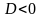- •Действия над матрицами. Определители. Решение систем линейных уравнений
- •Практическая работа 2 Выполнение действий над матрицами и решение систем линейных уравнений с помощью пакета Mathcad
- •Действия с комплексными числами.
- •Цель работы
- •Ход работы
- •Вариант
- •2. 2 Допуск к работе
- •Практическая работа 4 Выполнение действий над комплексными числами с помощью MathCad.
- •Допуск к работе
- •Практическая работа 5 Решение прикладных задач с помощью определённого интеграла в Mathcad.
- •3.2. Вариант
- •Решение дифференциальных уравнений первого и второго порядка
- •Цель работы
- •Ход работы
- •2.1 Вариант
- •Допуск к работе
- •Применение дифференциальных уравнений для решения прикладных задач
- •Практическая работа 8 Решение дифференциальных уравнений в Mathcad
- •3.2. Допуск к работе
- •4. Результаты работы
- •Числовые и степенные ряды.
- •Цель работы
- •2. Ход работы:
- •2.1 Вариант
- •2.2 Допуск к работе
- •Практическая работа 8 Обработка выборки в ms Excel
- •2.Оборудование:
- •4. Результаты работы.
- •4.8. Гистограмма.
- •5. Вывод
- •Точечные и интервальные оценки неизвестных параметров распределения
- •1. Цель работы
- •2.Оборудование:
- •3. Ход работы
- •5. Вывод
Ход работы
2.1 Вариант
Решите уравнение:
1) ____________________________________________________________________________________
2) ____________________________________________________________________________________
3) ____________________________________________________________________________________
4) ___________________________________________________________________________________
5) ____________________________________________________________________________________
6)____________________________________________________________________________________
7)____________________________________________________________________________________
8)____________________________________________________________________________________
9)____________________________________________________________________________________
10)___________________________________________________________________________________
______________________________________________________________________________________
______________________________________________________________________________________
Допуск к работе
2.2.1
Разделите переменные в уравнении:
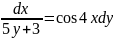
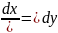
2.2.2
Вычислите
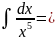
2.2.3
Решите уравнение
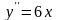
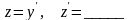
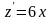
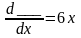
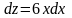
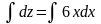





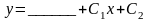
2.2.4 Продолжите равенства: a) ln 5 + ln 4 = ln 5∙4 = ln _____
б) ln(x+3) + lnC = _____________________
в) ln 12 = b ↔ 12 = e b
г) ln
z
= 5x
+ 8 ↔ z
=

д)
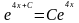
е)
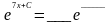
2.2.5
Известно общее решение дифференциального
уравнения
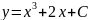 ,
найдите частное
решение, удовлетворяющее условию y
(-2)
=5
,
найдите частное
решение, удовлетворяющее условию y
(-2)
=5
______________________________________________________________________________________
2.2.4 Заполните таблицу:
Дифференциаль- ное уравнение |
|
||
Характеристичес- кое уравнение |
|
||
Дискриминант
|
|
|
|
Корни характеристичес-кого уравнения |
|
|
|
Общее решение дифференциаль- ного уравнения
|
|
|
|
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 7