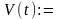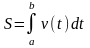3.2. Вариант

1. Скорость движения тела задаётся формулой 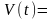. Найти путь пройденный телом за сек.

2. Вычислить силу давления на прямоугольную пластину с основанием

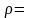
см и высотой см, погружённую вертикально в жидкость плотностью 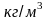так, что верхнее основание находиться на см ниже поверхности жидкости.

3. Силой 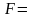Н пружина растягивается на см. Первоначальная длина пружины равна см. Какую работу надо совершить, чтобы растянуть пружину до см?

4. Найти объём тела, полученного при вращении кривой вокруг оси Ох, если

5. Найти площадь поверхности, полученной при вращении кривой вокруг оси Ох, если

6. Найти длину кривой между точками

7. Пластина в виде треугольника с основанием см и высотой см погружена в жидкость, плотности . Найти силу давления на пластину, если её вершина лежит на поверхности, а основание параллельно поверхности жидкости.

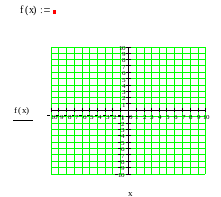
8. Найти площадь фигуры, ограниченной линиями:

, если

4. Результаты работы

1. 

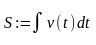
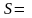
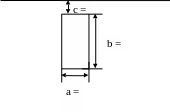
Основание (ширина пластинки f(x)) а= см = м

высота b= см = м

глубина погружения c= см = м

Нижний предел (с) -

Верхний предел (с+b) -

Р=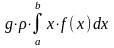

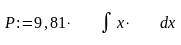
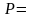
Cилой F= Н пружина растягивается на ∆x см = м

Коэффициент жёсткости пружины

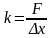
Пружина растягивается на b = см = м

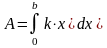
k : =

k =

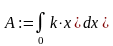
A=

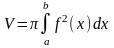
4.4

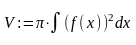
V=

4.5

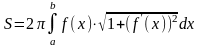
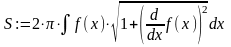
S=

4.6

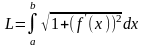
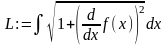
L =

4.7

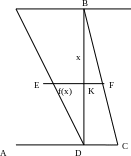
Основание AC = см = м

Высота BD = см = м

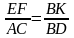
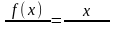
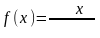
Р=

4.8

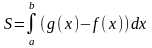
S=

5. Вывод

В ходе выполнения данной работы ________________________________________________________________________________________________________________________________________________________________________________________________________________________

ПРАКТИЧЕСКАЯ РАБОТА 6

Решение дифференциальных уравнений первого и второго порядка

1. Цель работы

1. Научиться решать дифференциальные уравнения первого порядка, с разделяющимися переменными.

2. Научиться решать дифференциальные уравнения второго порядка, допускающие понижение порядка

3. Научиться решать линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

4. Научиться применять дифференциальные уравнения для решения физических задач