1. Описание установки Судовой поршневой водяной насос

Электроприводные поршневые насосы устанавливаются на судах морского флота и предназначаются для перекачки жидкости и обслуживания системы пожаротушения.

Тип насоса - поршневой крейцкопфный электроприводной двухцилиндровый вертикальный трехскоростной. Кривошип 1 приводится во вращение асинхронным электродвигателем через редуктор и зубчатую передачу внешнего зацепления. Преобразование вращательного движения кривошипа в возвратно-поступательное движение поршней осуществляется двумя кривошипно-ползунными механизмами с общими стойками и коленчатым валом (кривошипом), двумя шатунами 2 и 4 и двумя поршнями3 и 5. Угол между коленами кривошипа составляет 180°. Вращательное движение кривошипа АОС преобразуется в возвратно-поступательное движение поршней 3 и 5.

Всасывание жидкости в цилиндры происходит во время хода поршня вверх через впускные клапаны, которые открываются автоматически при достижении в цилиндрах разрежения 0,05 МПа.

Открытие этих клапанов происходит в момент, соответствующий отходу кривошипов от верхней мертвой точки (ВМТ) на угол равный 15°. При достижении поршнем нижней мертвой точки (НМТ) впускной клапан закрывается и жидкость, поступившая в цилиндр, начинает сжиматься до Р_max. Когда кривошип АОС отойдет от нижней мертвой точки на 15°, толкатель кулачкового механизма открывает выпускной клапан и жидкость под давлением Р_max будет вытекать из цилиндра.

Кулачек закреплен на распределительном валу, который вращается с частотой вращения кривошипа АОС.

2. Синтез механизмов ц елью синтеза механизма является определение длин звеньев механизма

B` P

F

Н 3

V_ср

S`

B`` A`

2

1

n

A``

3

B

2

A

1

O

К подвижнымзвеньямотносят

1-кривошип

2-шатун

3-поршень

Найдём время 1-го оборота :

Где :

φ-угол поворота

ω-угловая скорость

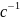
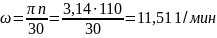
Вычисляем ход поршня :

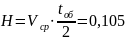м

Где 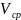- средняя скорость поршня

Длина кривошипа:

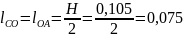м

Вычисляемдлину шатуна :

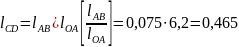м

где 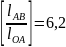- отношение длины шатуна к длине кривошипа

Вычисляем расстояние до центра тяжести :

м

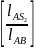где -отношение положения центра тяжести к длине шатуна.

3. Структурный анализ механизма

3

В

5 2

А

1

А

4 1

О

С

3

B

B_x

2

D

D_X

4

1

Данный механизм состоит из 5 подвижных звеньев и 1 неподвижной станины

К подвижным звеньям относятся :

1 -кривошип,

2;4 -шатуны,

3;5 -поршни.

В состав механизма входит 7 кинематических пар :

A(1;2),

B(2;3),

C(1;4),

D(4;5), Все кинематическиепары 5 класса

O(0;1),

Bx(3;0),

Dx(5;0).

Вычисляем степень подвижности механизма:

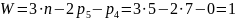
W=1 говорит о том, что в данном механизме одно ведущее звено.

Механизм компрессора состоит из: исходного механизма 1го класса и 2х структурных групп 2 класса 2-3;4-5.

B 3

5 Структурная группа 2-3;

с труктурная группа 4-5; 2го класса 2го вида

2го класса 2го вида А 2

4

Исходный механизм

1го класса

4.КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА НЕФТЯНОГО НАСОСА

Целью кинематического анализа является:

- определение положений звеньев;

- линейных и угловых скоростей звеньев;

- линейных и угловых ускорений звеньев.

1. .Построение плана положений механизма

Определим масштаб плана положений в соответствии ГОСТ 2302-68: масштабы уменьшения - µ_l=2∙10^-3 м/мм (М 1:2),

Реальные размеры звеньев механизма должны быть пересчитаны с учетом выбранного масштаба чертежа µ_l, т.е. определяются отрезки, изображающие на чертеже реальные длины звеньев

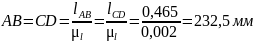
где l_OAи l_OC, l_ABи l_CD – реальные размеры кривошипа и шатунов, м.

4.2.Определение скоростей звеньев и шарниров механизма

Угловые и линейные скорости звеньев механизма и шарниров механизма определяем графоаналитическим методом, который называется методом планов. Метод планов основан на решении векторных уравнений для линейных скоростей (или ускорений), которые составляются для конкретной структурной группы механизма. Составление и решение векторных уравнений основано на методе Л. Эйлера.

Звенья, движущегося механизма, имеют различный характер движения - вращательное, параллельное и плоскопараллельное движение. Так движение кривошипа 1 - вращательное, поршней 3 и 5 - поступательное, а шатунов 2 и 4 - плоскопараллельное.

Рассмотрим движение исходного механизма, кривошип 1 совершает вращательное движение. Величина скорости т. А определяется по выражению

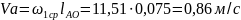
где 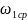-средняя угловая скорость кривошипа, ;

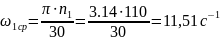
– длина кривошипа, м

n₁ – частота вращения.

Величина вектора скорости при вращательном движении направлена перпен­дикулярно звену АО в сторону вращения.

Определим масштаб плана скоростей ,

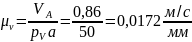где 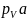- отрезок, который на плане скоростей изображает скорость точкиА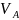 , мм. Это от­резок принимается равным =50 мм,

Определим скорости структурной группы 2-3. В нее входит шатун и поршень. Поскольку шатун 2 соверша­ет сложное плоскопараллельное движение, то для определения скорости т. В (кото­рая принадлежит и шатуну 2 и поршню 3) применяется уравнение Эйлера

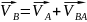
где - скорость переносной среды - скорость т. А (м/с), является известной по ве­личине и по направлению - перпендикулярна кривошипу ОА и направлена в сторо­ну вращения кривошипа;

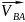~ относительная скорость т. В вокруг т. А, является неизвестной по величине и известной по направлению - скорость 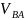перпендикулярна шатуну ВА

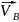- абсолютная скорость, скорость т. В относительно неподвижной опоры т. О, выступает неизвестной по величине и известной по направлению - вектор этой ско­рости параллелен оси цилиндра х-х.

Векторное уравнение содержит два неизвестных фактора - величины скоро­стей и , поэтому в данном виде решить его невозможно. Для его решения необходимо составить еще одно уравнение скорости т. В как принадлежащей посту­пательно движущемуся звену 3

где 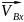-переносная скорость =0, т.к. ось цилиндра не перемещается. Здесь т. Вx - это точка, которая принадлежит оси цилиндра х-х, и временно совпадает с т. В, принадлежащей поршню;

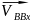- относительная скорость т. В относительно т. Вх, является неизвестной по ве­личине и известной по направлению - она параллельна оси цилиндра х-х.

В данном уравнении присутствует также два неизвестных. Для этого вектор­ные уравнения следует представить в виде системы уравнений

Из построенного плана скоростей получим искомые скорости

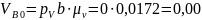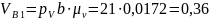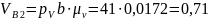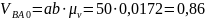м/с,

м/с,

м/с,

м/с,

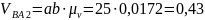м/с,

м/с,

где 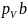, 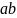- отрезки плана скоростей,которые определяются измерением. Скорость центра тяжести 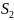шатуна АВ определяют следующим образом.

Из теоремы подобия отрезков следует

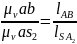
Из равенства необходимо сделать вывод: чтобы определить отрезок плана скоро­стей, который изображает относительную скорость необходимо отрезок bа плана скоростей, разделить в том же соотношении, в каком точка делит звено АВ. Полученный отрезок откладываем на плане скоростей и соединяем полученнуюточку с полюсом плана . Отрезок представляет собой скорость точки ее величина равна

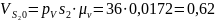м/с,

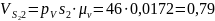м/с,

м/с.

По относительной скорости вычисляют угловую скорость шатуна 2, которая равна

;

;

;

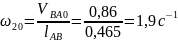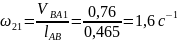Направление угловой скорости определяется по направлению скорости .

Определение скоростей структурной группы 4-5. Кривошип ОС смещен на 180°

от­носительно кривошипа АО исходного механизма АОС, который вращается с извест­ной угловой скоростью . Линейная скорость точки С кривошипа равна.

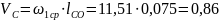м/с.

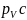Скорость перпендикулярна кривошипу ОС и направлена в сторону его враще­ния. Из полюса плана скоростей откладывают отрезок , который изображаетна плане скоростей скорость точки С. Длина этого отрезка определяется по зависи­мости

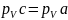
К исходному механизму АОС и неподвижной стойке при помощи кинемати­ческих пар присоединяется структурная группа 4-5. Для определения скорости шар­нира D воспользуется по аналогии со структурной группой 2-3 уравнениями Эйлера

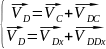
где 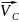- скорость переносной среды - скорость точкиС (м/с), является известной по величине и по направлению - перпендикулярна кривошипу ОС;

~ относительная скорость т. I) вокруг т. С, является неизвестной по величине и известной по направлению - скорость 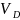перпендикулярна шатуну DС;

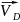-абсолютная скорость, скорость т. D относительно неподвижной опоры т.0,

выступает неизвестной по величине и известной по направлению - вектор этой ско­рости параллелен оси цилиндра х-х;

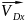- переносная скорость = 0, т.к. ось цилиндра не перемещается. Здесь т. Dх

-это точка, которая принадлежит оси цилиндра х-х, и временно совпадает с т. D принадлежащей поршню;

~относительная скорость т. D относительно т. Dх, является неизвестной по

величине и известной по направлению - она параллельна оси цилиндра х-х.

Из графического решения системы уравнений Эйлера - план скоростей, опре­деляют искомые скорости

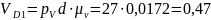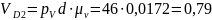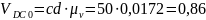м/с,

м/с,

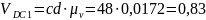м/с,

м/с,

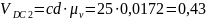м/с,

м/с,

где 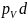, cd - отрезки плана скоростей, которые определяются измерением.

Из теоремы подобия отрезков следует

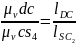
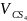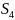Из равенства необходимо сделать вывод: чтобы определить отрезок плана скоро­стей, который изображает относительную скорость , необходимо отрезок cd плана скоростей, разделить в том же соотношении, в каком точка делит звено СD. Далее полученный отрезок 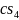откладываем на плане скоростей и соединяем полученную точку S₄ с полюсом плана . Отрезок представляет собой скорость точки ее величина равна

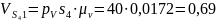м/с,

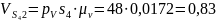м/с,

м/с.

По относительной скорости вычисляют угловую скорость шатуна 2, которая равна

;

;

;

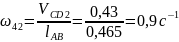Результаты вы­числений скоростей структурных групп для других положений кривошипа пред­ставлены в виде таблицы 4.1.