3.2. Організація рішення системи звичайних диференціальних рівнянь

Варто враховувати, що деякі різницеві схеми при певних кроках часу мають нестійкість (наприклад схема трапецій). У цих випадках необхідно проводити вибір кроку  з умови забезпечення стійкого рахунку.

П рийоми організації ітераційного рішення системи рівнянь (3.7) при лінійній постановці задачі відображені на рис.3.2.

Ітераційний процес здійснюється на кожному кроці часу. Для прискорення збіжності ітераційного процесу, в алгоритмах використовується попередня оцінка значень F, Y, Z для наступного моменту часу (прогноз). Для простоти використовуються значення, отримані на попередньому моменті часу.

Завершення ітераційного процесу відбувається при виконанні умов (3.8). Для здійснення цього вводяться робочі змінні YY, FF, ZZ. Крім того, уводиться робоча змінна G, значення якої є ознакою виконання умов (3.8). Спочатку кожної ітерації змінної G привласнюється значення 0. При невиконанні хоча б однієї з умов (3.8), значення G збільшується на 1. Ітераційний процес завершується, коли G наприкінці чергової ітерації залишається рівним 0.

О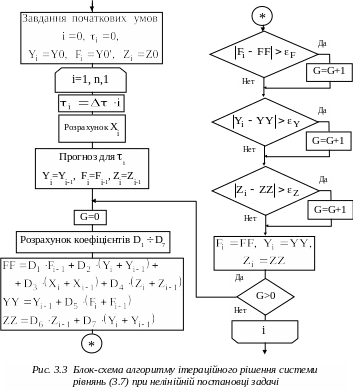 рганізація ітераційного рішення системи рівнянь (3.7) при нелінійній постановці задачі відображені на рис.3.3.

Систему алгебраїчних рівнянь (3.7), що відображає систему диференціальних рівнянь математичної моделі об'єкта (3.1), (3.2) зручніше вирішувати прямими методами. У цьому випадку не потрібно призначати абсолютні ітераційні допуски й не потрібно вести тривалі ітераційні процедури.

Однак виконання умов стійкості деяких використовуваних різницевих схем залишається в силі, що накладає обмеження на кроки часу .

Якщо використовуються прямі методи рішення задачі в лінійній постановці (рис.3.5), то попередньо формується незмінна матриця коефіцієнтів A. Вектор правої частини B уточнюється на кожному кроці часу .

Рис. 3.4 Блок-схема алгоритму прямого методу чисельного рішення системи рівнянь (3.4) (лінійна постановка задачі)

При рішенні задачі в нелінійній постановці (дивись рис. 3.3) значення коефіцієнтів матриці A і елементів вектора правої частини B уточнюються ітераційне на кожному кроці рішення.

Це необхідно, оскільки при рішенні нелінійної задачі значення коефіцієнтів рівнянь математичної моделі є функціями рішення. Тому, як наслідок, значення D1D7, а отже й значення коефіцієнтів матриці A й елементів вектора правої частини B так само є функціями рішення.

4. Рішення звичайних диференціальних рівнянь та їх систем в середовіщі excel

4.1. Організація рішення звичайних диференціальних рівнянь першого порядку

Розглядається рішення рівняння (4.1):

; , (4.1)

де - час,

X() - вплив на об'єкт,

У() - реакція об'єкту.

Вплив на об'єкт описується рівнянням (4.2)

. (4.2)

Для рішення (4.1) використовується різницева схема трапецій:

, (4.3)

де .

П риклад організації таблиці для рішення рівняння (4.1) наведений на рис. 4.1.

П 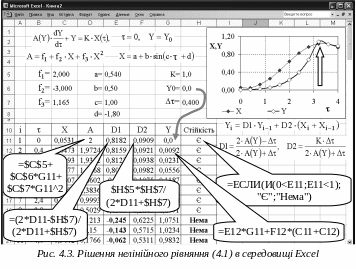риклад рішення рівняння (4.1), коли коефіцієнти рівняння є функціями рішення, наведений на рис. 4.3.

В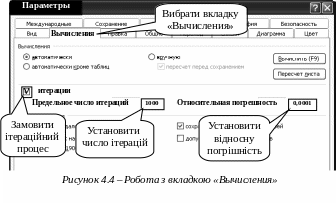 арто звернути увагу на використання ітераційного процесу для уточнення значень коефіцієнта A(Y) і потім уточнення рішення Y.

Для забезпечення виконання ітерацій необхідно звернутися до активного пункту меню " Сервис", потім до команди меню " Параметры" і працювати із вкладкою " Вычисления" як наведено на рис. 4.4.

З появою нестійкого рішення необхідно зменшити крок часу або використовувати іншу різницеву схему.