3. Рішення систем звичайних диференціальних рівнянь

3.1. Загальні положення

Якщо система звичайних диференціальних рівнянь містить рівняння, порядок яких вище першого, то попередньо виконується перетворення рівнянь порядку вище першого в систему звичайних диференціальних рівнянь першого порядку.

Потім вибирається один з різницевих методів і проводиться різницева апроксимація вихідних диференціальних рівнянь із використанням різницевих операторів. Тобто замість системи диференціальних рівнянь рішенню підлягає система лінійних алгебраїчних рівнянь

Алгоритм рішення отриманої системи алгебраїчних рівнянь розробляється залежно від типу різницевої схеми. Як правило, використання різницевих схем (крім явної різницевої схеми) вимагає організації ітераційного узгодження рішень окремих рівнянь. Для завершення ітераційних процесів використовуються умови, які потребують завдання значень абсолютних ітераційних допусків по кожної шуканій змінній. Цього можна уникнути, якщо використовувати прямі методи рішення отриманої системи лінійних алгебраїчних рівнянь.

Однак, при рішенні нелінійних задач, коли властивості системи (коефіцієнти в рівняннях математичних моделей) є функціями рішення, застосування ітераційних процесів необхідно.

Я к приклад, розглянемо динамічну систему, що складається із двох елементів (рис.3.1).

Математична модель системи:

; (3.1)

; (3.2)

Етап 1 Приведення математичної моделі об'єкта до системи звичайних диференціальних рівнянь 1- го порядку.

Уводиться нова змінна

. (3.3)

У результаті одержуємо систему рівнянь:

(3.4)

Етап 2 Запис кінцево-різницевих аналогів диференціальних рівнянь.

Використовується різницева схема трапецій.

,

(3.5)

Провівши формальні перетворення (3.5) одержимо:

(3.6)

У компактному записі:

,

, (3.7)

,

де

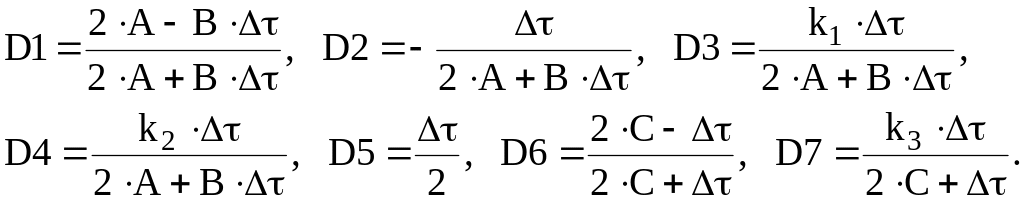
Етап 3. Рішення алгебраїчної системи рівнянь (3.7)

Р ішення (3.7) можна проводити ітераційне (наприклад методом Зейделя), але можна використовувати прямі методи (наприклад метод Гауса із провідним елементом). В останньому випадку формується матриця коефіцієнтів і вектор правих частин:

Fi	Yi	Zi
1	-D2	-D4
-D5	1	0
0	-D7	1

Якщо для рішення системи рівнянь (3.7) використовується ітераційний процес (наприклад метод Зейделя), то умовою закінчення ітераційного процесу на кожному кроці інтегрування буде одночасне виконання умов (3.8):

, , , (3.8)

де m - індекс ітерації,

F, Y, Z - абсолютні ітераційні допуски для змінних F, Y, Z.

Розглянуті підходи справедливі для будь-яких різницевих схем. Відмінність полягає тільки у вигляді розрахункових формул, використовуваних для визначення величини коефіцієнтів D.