5. Метод эквивалентного источника.

В основе метода эквивалентного источника лежит теорема об активном двухполюснике. Сущность метода заключается в том, что по отношению к выделенной ветви всю остальную часть схемы рассматривают как активный двухполюсник и она может быть заменена эквивалентным источником, т.е. расчет тока в выделенной ветви сведен к расчету тока по одной из схем рис.4 а, б.

R_H

E_H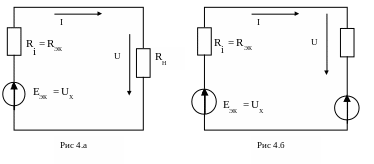

Eэк Ux

I = = схема рис 4.а

R_i + R_H Rэк + R_H

Eэк – E_H Ux- E_H

I = = схема рис 4.б

R_i+ R_H Rэк + R_H

Для исследования зависимости мощности нагрузки от сопротивления нагрузки воспользуемся теоремой об активном двухполюснике. Пусть произвольный активный двухполюсник подключен к сопротивлению R_H. Тогда в соответствии с теоремой об активном двухполюснике исходная схема может быть заменена эквивалентной ей схемой рис 4.а. Мощность сопротивления нагрузки определяется выражением

2

Eэк

P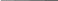 = I² · R_H = · R_H

R_i + R_H

Исследования этого выражения на экстремум в зависимости от R_H показывает, что значение мощности нагрузки будет иметь максимальное значение при условии R_H = R_I. В этом случае

E²_ЭК U²x

P _MAX = =

4R_i 4Rэк

U = 0,5 · Ux; I = 0,5 · I_K

Задача №1.

В схеме (рис.5) рассчитать значение тока I₃ методом наложения, считая параметры схемы (R, E, J) известными.

I₃

R₃

R₁

R₂ R₄

J₅

E₁

Рис.5

Решение

В соответствии с принципом наложения искомый ток

I₃=I_3(E)+I_3(J) , где

I_3(E) – ток в третьей ветви при действии в схеме источника E₁, а J₅=0

I_3(J) – ток в третьей ветви при действии в схеме источника J₅, а E₁=0

а) Расчет I_3(J)

Положим в исходной схеме J₅=0, тогда расчетная схема примет вид (рис.6а)

и определим в этой схеме I_3(E)

I_3(E) I_1(E)

I_1(E)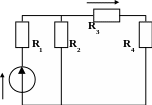

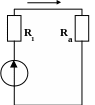
а) б)

Рис.6

Расчетная схема содержит один источник. В схеме с одним источником, как правило, рациональнее с точки зрения трудоемкости определять токи, упрощая схему путем эквивалентных преобразований пассивных ветвей.

В схеме (рис.6а) сопротивление R₂ включено параллельно с ветвью, состоящей из последовательно соединенных сопротивлений R₃ и R₄ .

Заменим сопротивления R₂, R₃, R₄ одним эквивалентным.

R₂(R₃+R₄)

Ra =

R₂+R₃+R₄

В результате получим схему (рис.6б). В этой схеме легко определить I_1(E) по закону Кирхгофа напряжений

I_1(E)R₁+I_1(E)Ra=E₁

или

E₁ E₁

I₁ = =

R₁+Ra R₂(R₃+R₄)

R₁ +

R₂+R₃+R₄

Для расчета тока I_3(E) вернемся к схеме рис.6а.

Ток I_3(E) определим по формуле деления тока на двух параллельных ветвях

R₂

I _3(E)= I_1(E)

R₂+R₃+R₄

Учитывая выражения для I_1(E), получим

E₁ R₂

I _3(E) = .

R₂(R₃+R₄) R₂+R₃+R₄

R₁ +

R₂+R₃+R₄

Величина

I_3(E) 1 R₂

G ₃₁= = . - передаточная проводимость между

E₁ R₂(R₃+R₄) R₂+R₃+R₄

R₁+

R₂+R₃+R₄

третьей и первой ветвями

б) Расчет I_3(J)

Положим в исходной схеме Е₁=0, тогда расчетная схема примет вид (рис.7а)

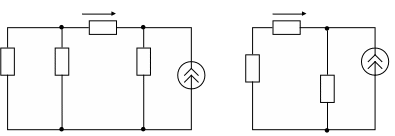
I_3(J) I_3(J)

R₃ R₃

R₁ R₂ R₄ R_b J₅

J₅

R₄

а) б)

Рис.7

Упростим схему, заменив параллельно соединенные сопротивления R₁ и R₂ одним эквивалентным R_b (рис.7б)

R₁R₂

R _b =

R₁+R₂

По формуле деления тока на двух параллельных ветвях

R₄

I _3(J)= - J₅

R_b+R₃+R₄

R₄

I _3(J)= - J₅

R₁R₂

+ R₃+R₄

R₁+R₂

Величина

I_3(J) R₄

T ₃₅= = - - коэффициент передачи по току между

J₅ R₁R₂

+ R₃+R₄

R₁+R₂

третьей и пятой ветвями.

Выражение для искомого тока I₃ в исходной схеме получим, если в выражение

I₃=I_3(E)+I_3(J)

подставить найденные значения I_3(E) и I_3(J)

Ток I₃ c использованием передаточных коэффициентов имеет вид

I₃=G₃₁E₁+T₃₅J₅

Задача №2.

В схеме рис.8 определить коэффициент передачи по напряжению H₇₁ и передаточные сопротивления по току R₉₅ и R₉₆ . Значение параметров схемы R,E,J – известны.

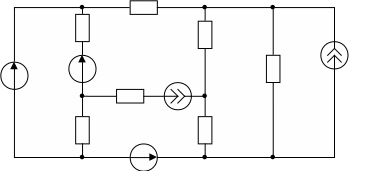
R₄

R₂ R₇

J₅

E₂ R₉

E₁ R₆

J₆

R₃ E₁₀ R₈

Рис.8

Решение.

а) Расчет коэффициента передачи по напряжению H₇₁

По определению

U₉

H₇₁ =

E₁

при условии, что все источники эдс, кроме E₁ и все источники тока равны нулю.

Где U₉ – напряжение на сопротивление R₉

Отразим эти условия на схеме (рис.9)

R₄

R₂ R₇

E₁ R₆ R₉

R₃ R₈

Рис.9.

После упрощения схемы получим (рис.10а,б)

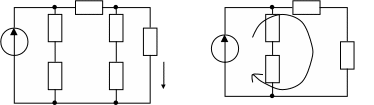R₄ R₄ I₄

R₇

R₂ R₂

E₁ R₉ E₁ Ra

R₃

R₃ R₈ I₉

1. б)

Рис.10

(R₇+R₈)R₉

Г де Rа=

R₇+R₈+R₉

По закону Кирхгофа напряжений (схема рис.10.б)

I₄(Rа+R₄)=E₁

E₁

I ₄=

Rа+R₄

Значение тока I₉ определим по правилу деления токов на двух параллельных ветвях (рис.10.а)

R₉+R₇

I ₉= I₄

R₇+R₈+R₉

Тогда U₉=I₉R₉ , или

E₁ (R₇+R₈)R₉

U ₉ = .

Ra+R₄ R₇+R₈+R₉

Окончательно

(R₇+R₈)R₉

H ₉₁=

(Ra+R₄)(R₇+R₈+R₉)

б) Расчет передаточного сопротивления R₉₅

По определению

R₉₅=U₉/J₅ , при условии, что все источники эдс и все источники тока, кроме J₅, равны нулю.

U₉=I₉R₉ – напряжение на сопротивлении R₉ при указанном выше условии.

Расчетная схема имеет вид (рис.11)

Рис.11

Так как последовательно соединенные сопротивления R₂, R₃ закорочены, то получаем схему (рис.12).

Рис.12

Параллельно источнику тока J₅ подключены три ветви R₄, (R₇+R₈) и R₉. Ток I₉ определим по формуле деления тока на n (n=3) параллельно соединенных сопротивлениях

1

R₉

I ₉= J₅

1 1 1

+ +

R₄ R₇+R₈ R₉

Тогда напряжение U₉=I₉R₉

1

U ₉= J₅

1 1 1

+ +

R₄ R₇+R₈ R₉

Либо напряжение U₉ определим по формуле

U₉=J₅Rэкв

1

Г де Rэкв = - эквивалентное сопротивление трех

1 1 1

+ +

R₄ R₇+R₈ R₉

параллельных ветвей относительно зажимов источника тока J₅

Окончательно

U₉ 1

R ₉₅= =

J₅ 1 1 1

+ +

R₄ R₇+R₈ R₉

в) Расчет передаточного сопротивления R₉₆

По определению R₉₆=U₉/J₆ при условии равенства нулю всех источников, кроме J₆

Расчетная схема представлена на рис.13.

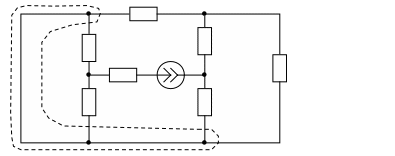
R₄

R₂ R₇

R₆ J₆ R₉

R₃ R₈

Рис.13.

Уже отмечалось, что, если схема содержит один источник, то, как правило, при расчете искомых токов схему упрощают, применяя эквивалентные преобразования пассивных ветвей. Отметим, что для расчета напряжения U₉ методом узловых потенциалов необходимо решить систему из двух уравнений

(К_МУП=У-1-В_е=4-1-0=2),

а методом контурных токов – из трех уравнений (К_МКТ=В-(У-1)-В_j=7-(4-1)-1=3)

Здесь B_e – количество ветвей, состоящих только из источников ЭДС.

В_i – количество ветвей с источниками тока.

Однако, как упростить схему (рис.13) не очевидно. Перерисуем эту схему, объединив в один узел (точку) узлы, обведенные пунктирной линией, в итоге получим (рис.14).

I₉

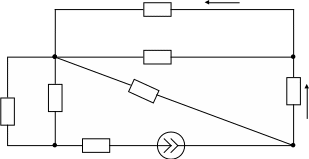
R₉

R₄

R₃ R₈ R₇ I₇

R₂

R₆ J₆

Рис.14

Выполнив эквивалентные преобразования, перейдем к схеме (рис.15)

I₇

Рис.15

R₉R₄ R₂R₃

Г де R_b = , R_C =

R₉+R₄ R₂+R₃

R₈

Т огда I₇ = J₆

R₇+R_b+R₆

и

R₈+R_b

U ₉= I₇R₆ = J₆

R₇+R₈+R_b

Искомое передаточное сопротивление

U₉ R₈+R_b

R ₉₆= =

J₆ R₇+R₈+R_b

Задача №3

Определить при каком значении сопротивления R_H (рис.16) на нем максимальная мощность и значение этой мощности. Параметры схемы (значение R, E, J) известны.

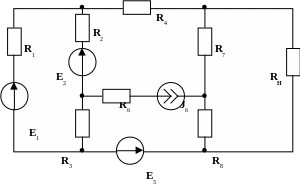
Рис.16

Решение.

Рассмотрим схему относительно зажимов сопротивления R_H как активный двухполюсник (схема рис.17).

R₄

a

R₂ R₇

R₁

E₂ U_x

R₆

I₇ IV

E₁

R₃ E₅ R₈ I₈

b

Рис.17

В соответствии с теоремой об активном двухполюснике, заменим активный двухполюсник на эквивалентный генератор напряжения и перейдем к эквивалентной схеме (рис.18)

а

R_i

R_H

I_H

E_эк

b

Рис.18

В этой схеме

E_эк

I _H=

R_i + R_H

E_эк

P _H= I²_H R_H=( ) ² R_H

R_i + R_H

Максимальное значение мощности на сопротивлении R_H будет при условии

R_H=R_i

и следовательно

E_эк E²_эк

P _HMAX =( )²R_i =

R_i + R_i 4R_i

Таким образом, для ответа на поставленные в задаче вопросы достаточно рассчитать параметры эквивалентного генератора R_i и E_эк.

а) Расчет E_эк

Значение эдс E_эк=U_x , где напряжение U_x – напряжение на разомкнутых зажимах активного двухполюсника (рис.17). Запишем уравнение по ЗКН для контура IV

U_x -I₇R₇ -I₈R₈=0, или

U_x= I₇R₇+I₈R₈

Определим токи I₇ и I₈ в двухполюснике при его разомкнутых зажимах. Нетрудно

показать, что расчет токов I₇ и I₈ (схема рис.19) рациональнее произвести методом контурных токов (количество совместно решаемых уравнений по МКТ

К_МКТ=В-(У-1)-В_i=6-(4-1)-1=2 , а по методу узловых потенциалов –

К_МУП=У – 1 – B_e=4 – 1 =3 )

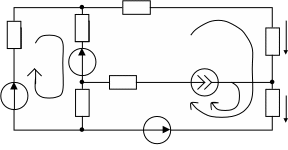
R₄

R₁ R₂ I_2k R₇ I₇

E₂

R₆ J₆

I_1k

R₃ I_3k R₈ I₈

E₁ E₅

Рис.19

I_1k(R₁+R₂+R₃) – I_2k(R₂+R₃) – I_3kR₃= E₁ – E₃

-I_1k(R₂+R₃)+I_2k(R₂+R₄+R₇+R₈+R₃)+I_3k(R₈+R₃)=E₂+E₅

I_1k=J₆

По этим уравнениям рассчитываем контурные токи I_1k и I_2k

Токи ветвей

I₇=I_2k

I₈=I_2k+I_3k

Таким образом, определили U_x

б) Расчет R_i

Сопротивление R_i=R_эк , где R_эк – эквивалентное сопротивление, рассчитанное относительно зажимов двухполюсника при условии, что все эдс источников напряжения и токи источников тока равны нулю. Схема для расчета R_эк представлена на рис.20.

R₄ a

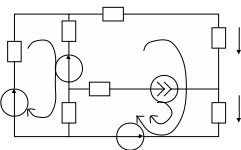R₁ R₂ R₇

R₃ R₈

b

Рис.20

Последовательность эквивалентных преобразований и соответствующие выражения представлены ниже.

a

R₄

R₇

Ra

R₈

b

Рис.21

R₁(R₂+R₃) (Ra+R₄)(R₇+R₈)

R a = R_экв=

R₁+R₂+R₃ Ra+R₄+R₇+R₈