
Клеточные матрицы
Рассмотрим некоторую матрицу А и разобьем ее на матрицы более низкого порядка:
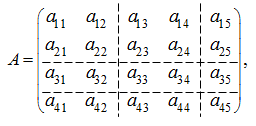
которые называются клетками или блоками.
Здесь клетками (блоками) являются матрицы:
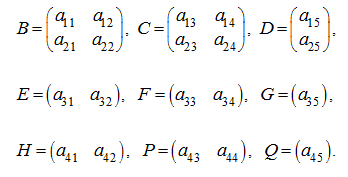
Теперь матрицу А можно рассматривать как клеточную или блочную:
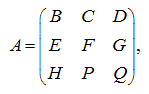
элементами которой являются клетки (блоки).
Очевидно, что разбиение произвольной матрицы на клетки (блоки) может быть выполнено различными способами. В частном случае клеточная матрица может оказаться квазидиагональной:
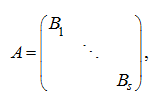
где
клетки ![]() –
квадратные матрицы (вообще говоря,
разных порядков), а вне клеток стоят
нули.
–
квадратные матрицы (вообще говоря,
разных порядков), а вне клеток стоят
нули.
Отметим,
что ![]()
Клеточные матрицы одной и той же размерности и с одинаковым разбиением называются конформными.
Действия над клеточными матрицами осуществляются по тем же правилам, что и над обычными матрицами.
1. Сложение и вычитание клеточных матриц
Пусть имеются две конформные клеточные матрицы:
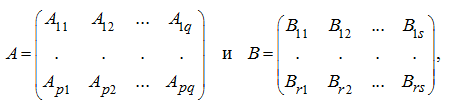
где p = r, q = s и
клетки ![]() одинаковой
размерности. Тогда
одинаковой
размерности. Тогда
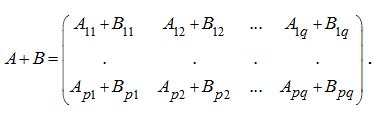
Аналогично выполняется вычитание клеточных матриц.
2. Умножение клеточных матриц
Умножение клеточной матрицы на число (скаляр)
Пусть А – клеточная матрица и h – число, тогда имеем:
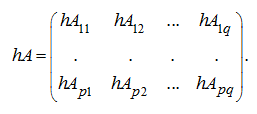
Умножение клеточных матриц
Рассмотрим две конформные клеточные матрицы:
причем q = r .
Пусть
все клетки ![]() такие,
что число столбцов клетки
такие,
что число столбцов клетки ![]() равно
числу строк клетки
равно
числу строк клетки ![]() (Например,
очевидно, что это имеет место в частном
случае, когда все клетки
–
квадратные матрицы и имеют одинаковый
порядок). Тогда легко показать, что
произведение матриц А и В –
тоже клеточная матрица:
(Например,
очевидно, что это имеет место в частном
случае, когда все клетки
–
квадратные матрицы и имеют одинаковый
порядок). Тогда легко показать, что
произведение матриц А и В –
тоже клеточная матрица:
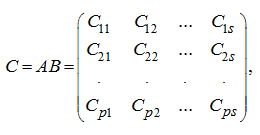
где ![]() то
есть умножение клеточных
матриц аналогично
умножению числовых [2].
то
есть умножение клеточных
матриц аналогично
умножению числовых [2].
П р и м е р . Перемножить клеточные матрицы

Р е ш е н и е .
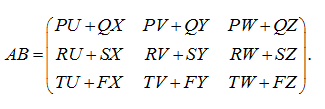
Треугольные матрицы
Квадратная матрица называется треугольной, если ее элементы, стоящие выше (ниже) главной диагонали, равны нулю. Например, матрица
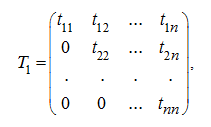
где ![]() является верхней
треугольной матрицей,
а матрица
является верхней
треугольной матрицей,
а матрица
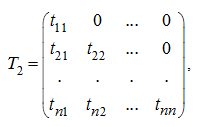
где![]() является нижней
треугольной матрицей.
Диагональная
матрица является частным случаем
треугольной матрицы (как верхней, так
и нижней). Очевидно, что определитель
треугольной матрицы равен произведению
ее диагональных элементов,
то есть в наших примерах:
является нижней
треугольной матрицей.
Диагональная
матрица является частным случаем
треугольной матрицы (как верхней, так
и нижней). Очевидно, что определитель
треугольной матрицы равен произведению
ее диагональных элементов,
то есть в наших примерах:
![]()
Поэтому треугольная матрица является невырожденной тогда и только тогда, когда все ее диагональные элементы отличны от нуля.
Сумма и произведение треугольных матриц одной и той же размерности и одинаковой структуры (то есть, обе – верхние, или обе – нижние) являются также треугольными матрицами той же размерности и структуры.
Обратная матрица невырожденной треугольной матрицы – также треугольная матрица той же размерности и структуры. Исходя из этого, обращение треугольной матрицы не вызывает никаких затруднений.
Элементарные преобразования матриц
Элементарные преобразования матрицы находят широкое применение в различных математических задачах. Например, они составляют основу известного метода Гаусса (метода исключения неизвестных) для решения системы линейных уравнений [1].
К элементарным преобразованиям относятся:
1) перестановка двух строк (столбцов);
2) умножение всех элементов строки (столбца) матрицы на некоторое число, не равное нулю;
3) сложение двух строк (столбцов) матрицы, умноженных на одно и то же число, отличное от нуля.
Две матрицы называются эквивалентными, если одна из них может быть получена из другой после конечного числа элементарных преобразований. В общем случае эквивалентные матрицы равными не являются, но имеют один и тот же ранг.
Вычисление определителей с помощью элементарных преобразований
С помощью элементарных преобразований легко вычислить определитель матрицы. Например, требуется вычислить определитель матрицы:

где ![]() ≠
0.
≠
0.
Тогда можно вынести множитель :
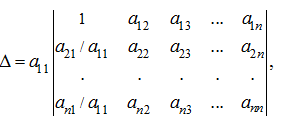
теперь,
вычитая из элементов j-го
столбца![]() соответствующие
элементы первого столбца, умноженные
на
соответствующие
элементы первого столбца, умноженные
на![]() ,
получим определитель:
,
получим определитель:
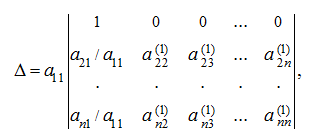
который
равен: ![]() где
где

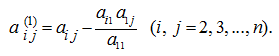
Затем
повторяем те же действия для ![]() и,
если все элементы
и,
если все элементы ![]() то
тогда окончательно получим:
то
тогда окончательно получим:
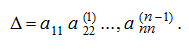
Если
для какого-нибудь промежуточного
определителя ![]() окажется,
что его левый верхний элемент
окажется,
что его левый верхний элемент![]() ,
то необходимо переставить строки или
столбцы в
так,
чтобы новый левый верхний элемент был
не равен нулю. Если Δ ≠ 0, то это всегда
можно сделать. При этом следует учитывать,
что знак определителя меняется в
зависимости от того, какой элемент
,
то необходимо переставить строки или
столбцы в
так,
чтобы новый левый верхний элемент был
не равен нулю. Если Δ ≠ 0, то это всегда
можно сделать. При этом следует учитывать,
что знак определителя меняется в
зависимости от того, какой элемент![]() является
главным (то есть, когда матрица
преобразована так, что
является
главным (то есть, когда матрица
преобразована так, что![]() ).
Тогда знак соответствующего определителя
равен
).
Тогда знак соответствующего определителя
равен![]() .
.
П р и м е р . С помощью элементарных преобразований привести матрицу
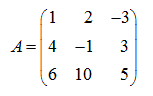
к треугольному виду.
Р е ш е н и е . Сначала умножим первую строку матрицы на 4, а вторую на (–1) и прибавим первую строку ко второй:
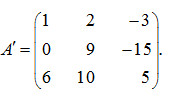
Теперь умножим первую строку на 6, а третью на (–1) и прибавим первую строку к третьей:
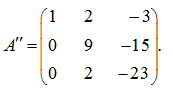
Наконец, умножим 2-ю строку на 2, а 3-ю на (–9) и прибавим вторую строку к третьей:
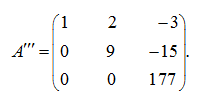
В
результате получена верхняя треугольная
матрица ![]()
Пример. Решить систему линейных уравнений, используя матричный аппарат:
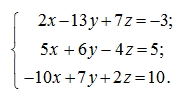
Р е ш е н и е. Запишем данную систему линейных уравнений в матричной форме:
![]()
где

Решение данной системы линейных уравнений в матричной форме имеет вид:
![]()
где ![]() –
матрица, обратная к матрице А.
–
матрица, обратная к матрице А.
Определитель матрицы коэффициентов А равен:
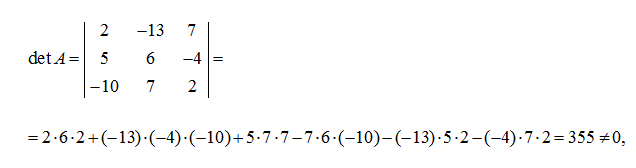
следовательно, матрица А имеет обратную матрицу .
Сначала найдем присоединенную матрицу Ã, которая в данном примере имеет вид:
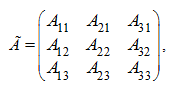
где![]() –
алгебраические дополнения соответствующих
элементов
–
алгебраические дополнения соответствующих
элементов![]() матрицы А.
матрицы А.
В нашем случае получим:
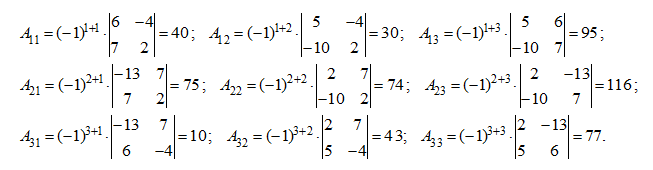
Таким образом,
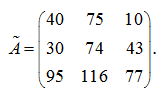
Тогда обратная матрица равна:
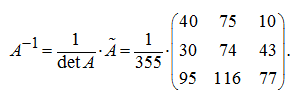
Теперь найдем решение заданной системы уравнений. Так как, то
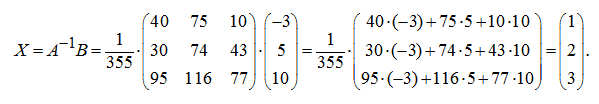
Таким
образом, решение данной системы
уравнений: ![]()
