Матричная алгебра. Введение

Матричная алгебра или матричное исчисление – раздел математики, посвященный работе с матрицами – одним из самых важных, употребительных и содержательных понятий в математике.

Матрицы – это, образно говоря, кирпичи и строительные блоки для построения и использования различных алгоритмов и математических моделей. С помощью матричного аппарата легко и удобно производить различные действия при решении задач линейной алгебры, системного анализа, динамики и прочности машин и механизмов, теории управления, экономики, статистики и других областей науки и знания, в том числе, решая системы линейных уравнений, производя векторные и линейные преобразования, используя теорию операторов и т.д. Сейчас даже трудно себе представить области, где бы не применялись матричные методы при решении различных задач.

В данном разделе в краткой форме изложены основные свойства, действия и методы работы с числовыми матрицами.

Основные определения

Система из mn чисел (действительных, комплексных), или функций, или других объектов, записанная в виде прямоугольной таблицы, состоящей из m строк и n столбцов:

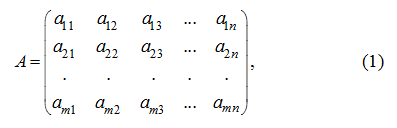
называется матрицей.

Числа (функции, другие объекты)  , составляющие матрицу (1), называются элементами матрицы. Здесь первый индекс  i  обозначает номер строки, а второй  j  – номер столбца, на пересечении которых расположен данный элемент матрицы.

Для матрицы (1) существует сокращенная запись:

или просто . В этом случае говорят, что матрица А имеет размерность m×n. Если m = n, то матрица называется квадратной порядка n. Если то матрица называется прямоугольной.

Матрица размерности 1×n называется вектором-строкой, а матрица размерности m×1– вектором-столбцом. Обычное число (скаляр) можно считать матрицей размерности 1×1.

Если квадратная матрица имеет вид:

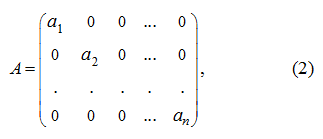
то она называется диагональной.

Если в диагональной матрице (2) все диагональные элементы равны 1, то матрица называется единичной и обозначается:

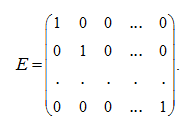
Используя символ Кронекера:

можно записать 

Матрица, у которой все элементы равны 0, называется нулевой и обозначается 0.

Элементы квадратной матрицы  n-го порядка образуют так называемую главную диагональ матрицы.Сумма элементов главной диагонали называется cледом (Trace, Spur) матрицы:

С квадратной числовой матрицей связано понятие определитель (детерминант):

Матрица и ее определитель разные (хотя и связанные) понятия. Числовая матрица А – это упорядоченная система чисел, записанная в виде прямоугольной таблицы, а ее определитель  det A – это число, равное:

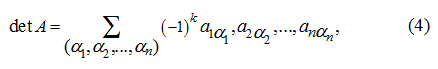
где сумма (4) распространяется на возможные перестановки элементов  1, 2,.., n и, следовательно, содержит n! слагаемых, причем k = 0, если перестановка четная и  k = 1, если перестановка нечетная.

П р и м е р .  Вычислить определитель матрицы

Р е ш е н и е .  Согласно (3) имеем:

Транспонированная матрица

Замена в матрице размерности  m×n

строк соответственно столбцами, дает так называемую транспонированную матрицу размерности  n×m :

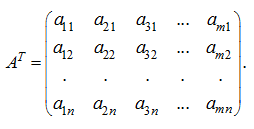
В частности, для вектора-строки транспонированной матрицей является вектор-столбец

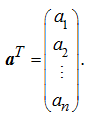
Основные свойства транспонированной матрицы:

1) дважды транспонированная матрица совпадает с исходной:

2) транспонированная матрица суммы матриц равна сумме транспонированных матриц слагаемых, то есть 

3) транспонированная матрица произведения матриц равна произведению транспонированных матриц сомножителей, взятому в обратном порядке:

Для квадратной матрицы имеет место очевидное равенство:

Если матрица совпадает со своей транспонированной

то она называется симметрической. Из последнего равенства следует, что симметрическая матрица является квадратной, и ее элементы, симметричные относительно главной диагонали, равны между собой: 

Очевидно, что произведение  является симметрической матрицей, так как, используя свойство 3, получим:

П р и м е р .  Даны матрица А и транспонированная матрица   :

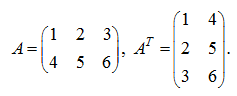
Вычислить произведения

Р е ш е н и е .

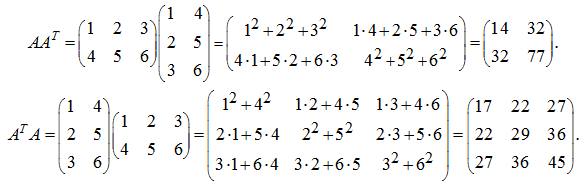
Как и следовало ожидать, получены симметрические матрицы.