
- •Электростатика Введение
- •§ 2. Поле объемных зарядов
- •3. Связь между потенциалом и напряженностью
- •§ 4. Потенциальные диаграммы
- •§ 5. Проводники в электростатическом поле
- •§ 6. Плотность заряда на поверхности проводника
- •§ 7. Электростатическая экранировка. Заземление
- •§ 8. Заряд и поле Земли
- •§ 9. Электростатический генератор, Линейные ускорители
- •§ 10. Электростатика(лазерные принтеры)
- •§ 11. Электростатика(Электрофильтры)
- •§ 12. Электростатика(Электрофорез)
- •§ 13. Электростатика(Коронный разряд)
- •§ 14. Электростатика(Теорема Гаусса)
- •§ 15. Электростатика(Конденсаторы)
- •Особенности построения вентильных преобразователей переменного тока в постоянный на базе полностью управляемых приборов и устройств
§ 2. Поле объемных зарядов
Напряженность поля, создаваемого объемными зарядами, обладает интересной особенностью: она возрастает при удалении от “центра тяжести” облака объемного заряда. Рассмотрим такое заряженное “облако”, имеющее форму шара (рис. 1). Общий заряд его обозначим д, объемная плотность заряда р предполагается постоянной.
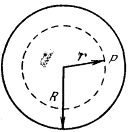 рис.
1
рис.
1
Найдем поле в точке Р внутри шара. Разобьем весь объемный заряд на две части: сферу радиуса г и остальную часть шара. Внешняя часть не создает никакого поля в точке Р. Это ясно из того, что ее можно представить себе состоящей из вложенных друг в друга концентрических заряженных сфер, а каждая из них, как мы доказали в предыдущем параграфе, не создает никакого поля в своей внутренней области. Поэтому остается только поле сферы радиуса r, которое равно Е=q/r2, где q - ее заряд, равный произведению плотности заряда р на объем: q=4/3pPir3. Следовательно, поле в точке Р равно Е=pr/3E0. Напряженность растет линейно с удалением от центра сферы. Как видно из вывода, этот рост объясняется тем, что при удалении от центра действующий заряд растет как г3, в то время как его поле убывает как 1/r2. Как только мы переходим в область r>R, т. е. выходим за пределы шара, заряд, создающий поле, перестает возрастать и поле убывает обратно пропорционально r2.
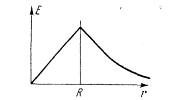 рис.
2
рис.
2
Рассмотрим теперь, как меняется с расстоянием напряженность поля, создаваемого бесконечным плоским объемно заряженным слоем.
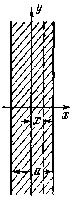 рис.
3
рис.
3
Его можно мысленно разбить на ряд тонких параллельных плоскостей. Поле плоскости равно 2л и не зависит от расстояния до нее, поэтому поля отдельных плоскостей будут просто складываться. Это значит, что будут складываться заряды, приходящиеся на единицу площади. Общий заряд, приходящийся на единицу площади слева от пунктирной плоскости, будет равен (a/2+x) • 1 • p, а справа (a/2 - x) • 1 • p. Значит, поле, создаваемое зарядом, находящимся слева от пунктирной плоскости, равно 2p Pi(a/2+x), а поле заряда, находящегося справа, 2Pip(a/2-x). Направлены эти поля в противоположные стороны, поэтому результирующее поле будет равно их разности 4pPix. Итак, внутри слоя
E=px/E0
На границе слоя х = а/2 и Е=2pPiа. Это последнее значение
совпадает с 2л@, (@-сигма)так как на
единицу площади слоя приходится заряд,
равный a • 1 • p.Получается зависимость
Е от x, представленная
на рисунке 4.
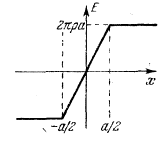 рис.
4
рис.
4
Конец формы
3. Связь между потенциалом и напряженностью
Из формулы A12=q(1-2) нетрудно получить связь между потенциалом и напряженностью поля. Пусть точки 1 и 2 соединяет малый вектор (delta)l.Работу поля над зарядом q на участке можно вы-числить двумя способами. Во-первых, ввиду малости вектора (delta)l мы . можем считать силу qE на всем его протяжении постоянной по величине и направлению и вычислять работу как FS cos, т. е. в данном случае qE(delta)lcos. С другой стороны, эта же работа равна, как мы по-казали в предыдущем параграфе, q(1-2)= -q(delta), где (delta)= 2-1 есть разность меж-ду конечным и начальным значениями потенциала. При-равнивая два выражения для работы, получим (delta) = -E(delta)lcos.
Эта формула определяет разность потенциалов между двумя близкими точками, соединенными малым векто-ром (delta)l, составляющимоуголе?ястнапряженностьюнполяоЕ.
Используя введенное в § 13 понятие скалярного про-изведения векторов, запишем (27.1) в более компактном виде:
(delta) = -E(delta)l.
Если поле однородное, можно в качестве (delta)l взять лю-бую, не обязательно малую, длину. Например, разность потенциалов между двумя точками внутри плоского конденсатора (рис. 5) равна ф2-ф1 =-El cos а. Если отрезок I соединяет пластины и направлен нормально к ним, т. е. вдоль линий напряженности поля, то (ф2- ф1 = -El, ИЛИ
E=(ф1-ф2)/l (27.4)
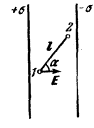 рис.
5
рис.
5
Если соотношения (27.2) или (27.1) выражают
потенциал через напряженность, то (27.3)
выражает напряженность через потенциал
(в частном случае однородного поля).
 рис.
6
рис.
6
Напряженность можно выразить через потенциал и в общем случае любого поля (разумеется, потенциального). Для этого возьмем в формулах (27.1) или (27.2) вектор delta l, параллельный Е. Тогда получим delta ф = -Е • delta1, или
E= -delta ф/delta l (27.4)
Выражение delta ф/delta l , очевидно, имеет смысл падения потенциала, приходящегося на единицу длины.
Формулы (27.3) и (27.4) имеют одинаковый вид в гауссовой системе и в системе СИ. Размерность напряженности в системе СИ, как было уже доказано, в/м. Эта размерность наглядно видна из
формул (27.3) и (27.4).
Эквипотенциальные поверхности.
Точки, в которых потенциал имеет заданное фиксированное значение, располагаются на поверхностях, называемых эквипотенциальными поверхностями (рис. 70). Нетрудно доказать, что линии напряженности перпендикулярны к этим поверхностям. Для этого применим формулу delta ф = -Е delta l cos а к вектору delta l, лежащему в одной из эквипотенциальных поверхностен (см. рис. 6). Естественно, что разность потенциалов delta ф между его началом и концом равна нулю (так как обе точки лежат на одной эквипотенциальной поверхности). Это значит, что cos a = 0, т. е. а = Pi/2 и Е перпендикулярен delta l.
Например, эквипотенциальные поверхности поля точечного заряда представляют собой концентрические сферы, а линии напряженности исходящие из центра лучи (рис. 7, а). Эквипотенциальные поверхности поля плоского конденсатора-плоскости, параллельные пластинам, а линии напряженности - прямые, к ним пер-пендикулярные (рис. 7, 6).
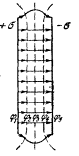 рис.
7(б)
рис.
7(б)
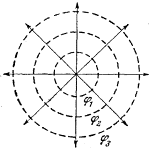 рис.
7(а)
рис.
7(а)
Изменение потенциала при переходе от одной эквипотенциальной поверхности к другой одинаково при перемещении на любой вектор, соединяющий эти поверх-ности. Самым коротким из них является тот, который
нормален к эквипотенциальным поверхностям. По этому направлению потенциал меняется наиболее быстро. Следовательно, наиболее быстро потенциал меняется вдоль линии напряженности.
Формулу Е = - delta ф/deltal читают так: напряженность есть минус градиент потенциала. Градиентом скалярной величины называется вектор, имеющий направление наиболее быстрого возрастания этой величины, а по модулю равный ее изменению на единицу длины.
Типичный метод решения электростатических задач. Введение понятия потенциала чрезвычайно упростило решение электростатических задач. Зная потенциал, можно уже легко найти другие электрические величины - напряженность, емкость и др.
Для определения потенциала любой системы заряженных тел можно написать уравнение, которое непосредственно выражает потенциал через имеющиеся заряды (уравнение Пуассона или его частный случаи • уравнение Лапласа). Это уравнение - не алгебраическое, а дифференциальное уравнение в частных производных, поэтому здесь мы не выписываем его. Точное решение уравнения Лапласа можно получить в редких случаях. Один из них, и весьма важный, - поле заряженного эллипсоида.
Весьма облегчает решение электростатических задач принцип однозначности решения. Каким бы способом, хотя бы и путем догадки, мы ни нашли решение задачи, но если найденный потенциал удовлетворяет уравнению Лапласа и граничным условиям, то решение является правильным и единственным. Значение этого принципа мы проиллюстрируем далее (§ 4) на важном электростатическом методе, называемом методом зеркальных изображений.
