2.1 Вариант

1. Найдите первые три члена ряда : .

2. Определить сходится или расходится данный геометрический ряд :

3. Определить сходится или расходится данный гармонический ряд :

4. Выполняется ли необходимый признак сходимости у ряда :

5. С помощью предельного признака исследовать ряд :

6. С помощью признака Даламбера исследовать сходимость ряда : .

7. С помощью признака Коши исследовать сходимость ряда :

8. Исследовать на сходимость знакочередующийся ряд. Если ряд сходятся, то определить, сходятся он абсолютно или условно.

9. Разложите многочлен по степеням .

10. Написать первые три, отличные от нуля, члена разложения по степеням х функции

11. Разложите функции в степенной ряд используя разложение элементарных функций и определите интервал сходимости:

1. 

2. 

3. 

2.2 Допуск к работе

Заполните пропуски:

2.2.1 Дан ряд пятый член ряда:

2.2.2 Ряд вида называется геометрическим рядом.

Геометрический ряд:

1. ______________________ при ;

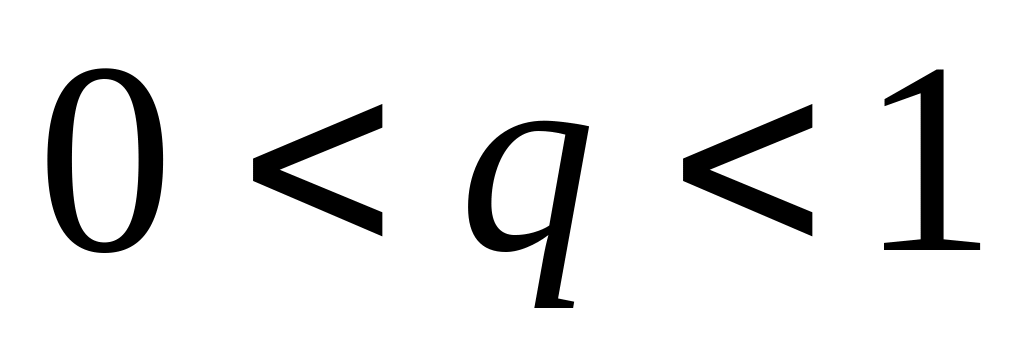2. расходится при .

2.2.3 Ряд вида называется обобщённым гармоническим рядом.

Гармонический ряд:

1. сходится при ;

2. _____________ при .

2.2.4 Если ряд сходится, то его общий член стремится к _________ т.е. .

2.2.5 Вопрос о сходимости рядов вида , где - многочлен от n степени k, a - многочлен от n степени l, полностью исчерпывается сравнением с рядом , где .

2.2.6 Предельный признак сравнения. Если для положительных рядов

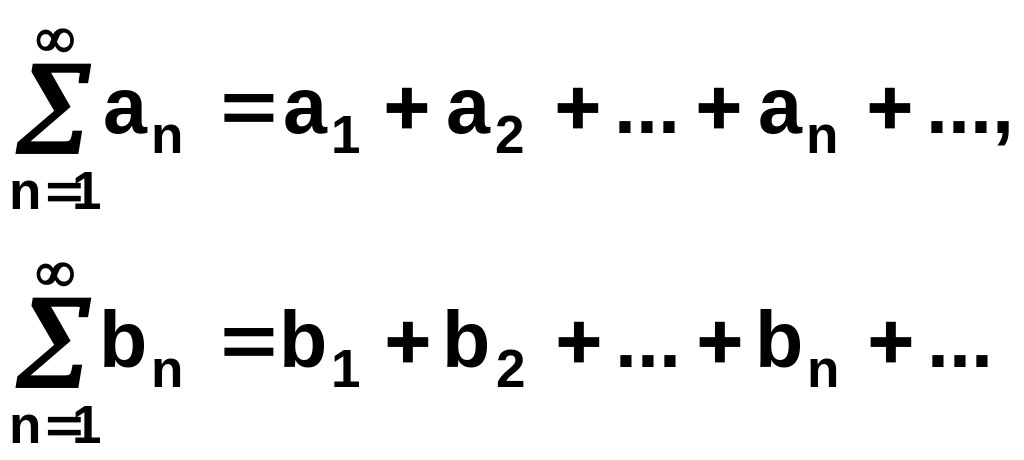
существует конечный

то эти ряды сходятся или расходятся ____________________.

2.2.7 Признак Даламбера. Если члены положительного ряда таковы, что существует предел , то при ряд сходится, а при ряд расходится.

2.2.8 Признак Коши. Если члены положительного ряда таковы, что существует предел , то при ряд _____________ , а при ряд _______________

2.2.9 ПризнакЛейбница . Если члены ряда

,

где , по абсолютной величине монотонно ______________ ,

и их общий член стремится к ________

,

то ряд сходится. При этом его сумма – положительное число, меньше первого члена этого ряда.

2.2.10 Знакочередующийся ряд называется ________________________________ , если сходится ряд, составленный из модулей его членов. Знакочередующийся ряд называется условно сходящимся, если он____________ , а ряд, составленный из модулей его членов, _____________.

2.2.11 Ряд

называется рядом Тейлора функции в точке .

2.2.12 Если в ряде Тейлора положим , то получим частный случай ряда Тейлора, который называют рядом Маклорена:

.

К работе допускается ______________

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 19

Разложение функций в ряды и

исследование рядов на сходимость с помощью Mathcad.

1. Цель работы

1. Научиться исследовать числовые ряды на сходимость с помощью пакета Mathcad;

2. Научиться находить радиус и область сходимости степенного ряда с помощью пакета Mathcad.

3. Научиться раскладывать функцию в ряд Тейлора и Маклорена с помощью пакета Mathcad.

2. Оборудование

Пакет программ MathCAD

3. Ход работы: