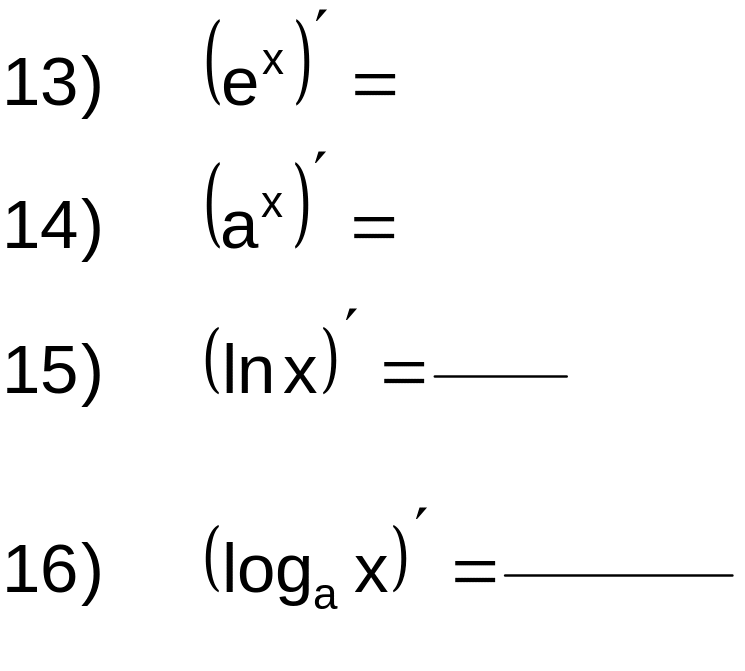- •Содержание
- •2. Найти производную второго порядка
- •2.1 Вариант
- •3.1 Вариант
- •3.1 Вариант
- •Практическая работа 21 Комплексные числа.
- •Цель работы
- •Ход работы
- •Вариант
- •2. 2 Допуск к работе
- •Практическая работа 22 Выполнение действий над комплексными числами с помощью MathCad.
- •Допуск к работе
- •Результаты работы
- •5. Вывод
Бюджетное профессиональное образовательное учреждение
Вологодской области
«Череповецкий металлургический колледж имени академика И.П. Бардина»

Специальность 230115 «Программирование в компьютерных системах»
ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Отчеты
ПР. 230115. 00. 00
Проверил: Масыгина И.А.
преподаватель колледжа
Подпись_____________
Выполнил: ___________
студент группы 2-ПКС
Подпись_____________
2014-2015 уч.год
Содержание

Практическая работа № 1:Действия над матрицами. Определители. Метод Крамера ………. |
|
Практическая работа № 2: Обратная матрица. Решение систем линейных уравнений методом обратной матрицы и методом Гаусса …………………………………………………. |
|
Практическая работа № 3: Выполнение действий над матрицами и решение систем линейных уравнений с помощью Mathcad……............................................................................. |
|
Практическая работа № 4:Решение задач аналитической геометрии с помощью Mathcad …. |
|
Практическая работа № 5: Уравнение прямой на плоскости ………………………………….. |
|
Практическая работа № 6: Составление уравнений кривых второго порядка………............... |
|
Практическая работа № 7: Расчёт параметров кривых второго порядка с помощью Mathcad |
|
Практическая работа № 8: Применение производной ………………………………………….. |
|
Практическая работа № 9: Частные производные ……………………………………………… |
|
Практическая работа № 10: Решение задач дифференциального исчисления с помощью Mathcad …………………………………………………………………………………………….. |
|
Практическая работа № 11: Нахождение неопределённых, определённых и несобственных интегралов………………………………………………………………………………………….. |
|
Практическая работа № 12:Решение прикладных задач с помощью определённого интеграла в Mathcad ……………………………………………………………………………… |
|
Практическая работа № 13:Вычисление двойных интегралов ………………………………… |
|
Практическая работа № 14: Решение дифференциальных уравнений первого порядка…....... |
|
Практическая работа № 15: Решение дифференциальных уравнений второго порядка……… |
|
Практическая работа № 16: Применение дифференциальных уравнений для решения прикладных задач ………………………………………………………………………………… |
|
Практическая работа № 17: Решение дифференциальных уравнений в Mathcad……………. |
|
Практическая работа № 18: Числовые и степенные ряды……………………………………… |
|
Практическая работа № 19: Разложение функций в ряды и исследование рядов на сходимость с помощью Mathcad ………………………………………………………………… |
|
Практическая работа № 20: Приближённые вычисления с помощью рядов с использованием Mathcad и Excel …………………………………………………………………………………… |
|
Практическая работа № 21: Комплексные числа ………………………………………………. |
|
Практическая работа № 22: Выполнение действий над комплексными числами с помощью Mathcad…………………………………………………………………………………………….. |
|
ПРАКТИЧЕСКАЯ РАБОТА 1
Действия над матрицами. Определители. Метод Крамера.
Цель работы
Научиться выполнять сложение матриц, умножение матриц на число,
умножение матриц и вычислять определители.
1.2 Научиться решать системы линейных уравнений методом Крамера.
Ход работы
Вариант
Даны матицы
 ,
,
 ,
,

Найти:
Решить систему линейных уравнений методом Крамера
2.1.5.
2.1.6
Допуск к работе
Для данной матрицы

А) Выпишите элементы главной диагонали: ___________________________________
 Б)
Выпишите элемент третьей строки второго
столбца: __________________________
Б)
Выпишите элемент третьей строки второго
столбца: __________________________
Вычислите:
А)
![]() =
=
Б)
![]()
В)
![]()
Сформулируйте кратко правило нахождения произведения матриц.
________________________________________________________________________________________________________________________________________________
Вычислите произведение матриц
![]() =
=![]() =
=
Как вычислить определитель второго порядка?
![]()
Как вычислить определитель третьего порядка по схеме треугольников?


Для данной матрицы
А) Вычислите: М13 = ________________
Б) Вычислите: А13 = _________________
В) Вычислите: А23 = _________________
Как разложить определитель по элементам столбца или строки?
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Запишите формулы Крамера для решения систем линейных уравнений?
![]()
![]()
К работе допускается ______________
ПРАКТИЧЕСКАЯ РАБОТА 2
Обратная матрица. Решение систем линейных уравнений методом обратной матрицы и методом Гаусса
Цель работы
Научиться находить матрицу, обратную данной и решать системы линейных
уравнений в матричной форме и методом Гаусса.
Ход работы
Вариант
Вычислить обратные матрицы для данных:
2.1.1.1.
![]() ;
;
2.1.1.2. .
Решить матричным способом систему уравнений:
2.1.2.1.
![]()
2.1.2.2.
![]()
Решить систему уравнений методом Гаусса:
2.1.3.1.
2.1.3.2.
Допуск к работе
Запишите единичную матрицу третьего порядка.

Какая матрица называется обратной по отношению к данной?
________________________________________________________________________________________________________________________________________________________________________________________________________________________
Транспонируйте матрицу?
А= АТ =
Заполните пропуски:
Для нахождения обратной матрицы используют следующую схему:
Находят ____________________ матрицы А. т. е.
 .
.Находят __________________________________А ij всех элементов аij матрицы А.
Из вычисленных алгебраических дополнений составляем матрицу
 .
.Транспонируем полученную матрицу:
 .
.Вычисляем обратную матрицу А-1, _____________ каждый элемент последней из полученных матриц на
 .
.
Для данной системы линейных уравнений составьте матрицы: А, В, Х
![]()
 ,
,
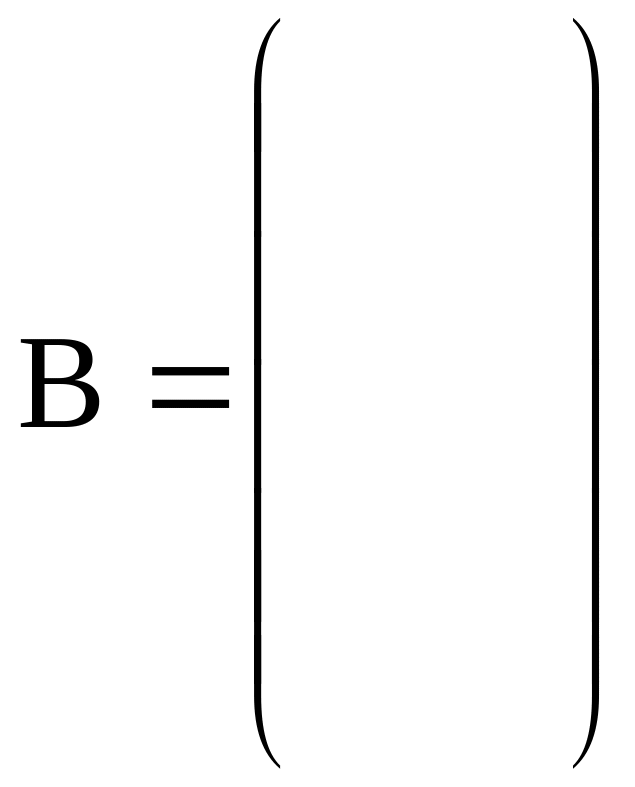 ,
,
 .
.
В каком случае обратная матрица не существует?
________________________________________________________________________________________________________________________________________________
2.2.7 Решите систему
![]()
К работе допускается ______________
ПРАКТИЧЕСКАЯ РАБОТА 3
Выполнение действий над матрицами и решение систем линейных уравнений с помощью пакета MathCAD.
Цель работы
Научиться выполнять действия над матрицами и решать системы линейных уравнений с помощью пакета MathCAD.
Оборудование
Пакет программ MathCAD.
Ход работы
3.1. Вариант
Даны
матрицы:
![]() ;
;
![]() ;
;
![]() .
.
Найти:
3.1.1.
3.1.2.
3.1.3.
Дана матрица:
![]()
 .
.
Найти:
3.1.4.
3.1.5.
3.1.6.
Решите матричное уравнение
 ,
если
,
если
 ,
,
 .
.Решите данную систему уравнений:

 Допуск
к работе
Допуск
к работе
Как вывести на экран панель математических инструментов (Math Palette)?
______________________________________________________________________________________________________________________________________________
Какая кнопка открывает панель простейших вычислений?
______________________________________________________________________________________________________________________________________________
Какая кнопка открывает панель векторных и матричных операций?
______________________________________________________________________________________________________________________________________________
Комбинацией каких клавиш задаётся знак присваивания?
______________________________________________________________________________________________________________________________________________
Как задаётся число строк и столбцов вводимой матрицы?
______________________________________________________________________________________________________________________________________________
Как вводятся элементы матрицы?
______________________________________________________________________________________________________________________________________________
За какой кнопкой на панели векторных и матричных операций закреплена функция вычисления определителя матрицы?
______________________________________________________________________________________________________________________________________________
За какой кнопкой на панели векторных и матричных операций закреплена функция транспонирования матрицы?
_______________________________________________________________________ _______________________________________________________________________
За какой кнопкой на панели векторных и матричных операций закреплена функция, позволяющая вычислить обратную матрицу?
________________________________________________________________________________________________________________________________________________
На какой панели находится кнопка с функцией, позволяющей возвести матрицу в квадрат?
________________________________________________________________________________________________________________________________________________
К работе допускается ____________
Результаты работы
4.8.
5. Вывод
В ходе выполнения данной работы ________________________________________________________________________________________________________________________________________________________________________________________________________________________
ПРАКТИЧЕСКАЯ РАБОТА 4
Решение задач аналитической геометрии с помощью Mathcad
Цель работы
Научиться выполнять действия с векторами в Mathcad.
Научиться решать задачи аналитической геометрии в Mathcad.
Ход работы
Вариант
Даны точки А( ; ; ), В( ; ; ), С( ; ; ), Д( ; ; ) найти
Координаты вектора
 ;
;Координаты вектора
 ;
;Координаты вектора
 ;
;Длину вектора
Длину вектора
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Косинус угла между векторами
Проекцию вектора
Даны точки А( ; ; ), В( ; ; ), С( ; ; ) найти
Периметр треугольника АВС;
Площадь треугольника АВС;
Длину средней линии ║ ;
Длину высоты;
Длину медианы.
Допуск к работе
.
Сформулируйте правило вычисления координат вектора, если известны координаты его начала и конца .
______________________________________________________________________________________________________________________________________________
Пусть известны координаты точек А(ха; уа; za ) и В(хb; уb; zb ). Запишите формулы для вычисления:
А) Координат
вектора
![]() _______________________________________
_______________________________________
Б) Расстояния АВ ______________________________________________
В) Координаты точки С – середины отрезка АВ
![]() ,
,
![]() ,
,
![]()
Пусть известны координаты векторов
 (ах;
ау;
аz
) и
(ах;
ау;
аz
) и
 (bx;
by;
bz
),
(bx;
by;
bz
),
![]() (сx;
сy;
сz
). Запишите формулы для вычисления:
(сx;
сy;
сz
). Запишите формулы для вычисления:
A)
Координат вектора
![]() ___________________________________
___________________________________
Б) Координат
вектора
![]() ___________________________________
___________________________________
В) Скалярного произведения векторов и _______________________
Г) Векторного произведения векторов и _______________________

Д) Векторного произведения
векторов
,
и
![]() __________________
__________________

Д) Проекции вектора на вектор ________________________________
Запишите формулу Герона для вычисления площади треугольника
_____________________________________________________________
Выразите высоту треугольник из формулы площади

_____________________________________________________________
Сформулируйте свойство средней линии треугольника.
______________________________________________________________________________________________________________________________________________
Дайте определение медианы треугольника.
______________________________________________________________________________________________________________________________________________
К работе допускается ______________
ПРАКТИЧЕСКАЯ РАБОТА 5
Уравнение прямой на плоскости
Цель работы
Научиться оставлять уравнения прямых на плоскости
Научиться применять MathCAD для составления уравнения прямых на плоскости
Оборудование
Пакет программ MathCAD.
Ход работы
3. 1. Вариант
Дан треугольник АВС: А( ; ), В( ; ), С( ; )
Найти
Уравнения сторон АВ, АС, ВС
Уравнения медиан AD, CM, BK
Уравнения средних линий
DM параллельной AC
MK параллельной BC
KD параллельной AB
Уравнения высот AN, BH, CE
Допуск к работе
Запишите общее уравнение прямой __________________________________
Выберите верные подписи к рисункам (нормальны вектор, направляющий вектор)

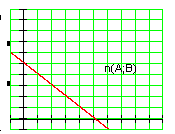

________________________вектор_____ ________________________вектор____
Прямая задана уравнением 5х - 4у + 6 = 0
А) Запишите
координаты нормального вектора
![]() ____________
____________
Б) Запишите
координаты направляющего вектора
![]() __________
__________
Продолжите предложения:
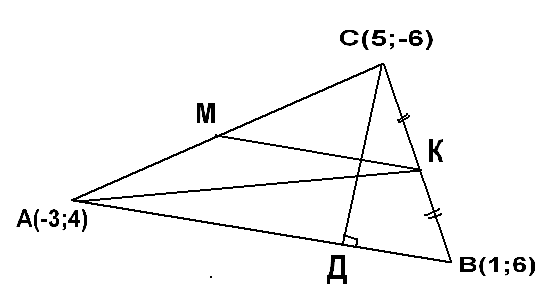
А) Направляющим вектором прямой АВ является вектор __________
Б) Нормальным вектором прямой СД является вектор __________
В) Если МК – средняя линия треугольника АВС, параллельная стороне АВ, то направляющим вектором прямой МК является вектор _______________________
Г) Если АК – медиана треугольника АВС, К – середина стороны ___________
Известно общее уравнение прямой Ах + Ву +23 = 0
А) Направляющим
вектором её является вектор
![]() запишите
уравнение прямой
запишите
уравнение прямой
__________________________________________________________________________
Б) Нормальным
вектором её является вектор
![]() запишите
уравнение прямой
запишите
уравнение прямой
____________________________________________________________________________
Известно, что прямая 5х + 4у + С = 0 проходит через точку Д(-3; 2) найдите С
_______________________________________________________________________
Пусть известны координаты точек А(ха; уа ) и В(хb; уb). Запишите уравнение прямой, проходящей через две точки
![]()
Пусть известны координаты точек А(3; -8 ) и В(4; 5). Запишите уравнение прямой, проходящей через две точки
![]()
_________________________________________________________________
К работе допускается ______________
ПРАКТИЧЕСКАЯ РАБОТА 6
Составление уравнения кривых второго порядка.
Цель работы
Научиться составлять уравнения кривых второго порядка
Ход работы
2.1. Вариант
Составить уравнение окружности, ______________________________________
________________________________________________________________
_______________________________________________________________ . Сделать чертёж.
Составить уравнение окружности, ______________________________________
________________________________________________________________
_______________________________________________________________ Сделать чертёж.
Составить уравнение эллипса ________________________________________
________________________________________________________________
_______________________________________________________________ Сделать чертёж.
Составить уравнение эллипса ________________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
Составить уравнение гиперболы ______________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
Составить уравнение гиперболы______________________________________
________________________________________________________________
_______________________________________________________________.
Сделать чертёж.
Составить уравнение эллипса, ______________________________________
________________________________________________________________
_______________________________________________________________..Сделать чертёж.
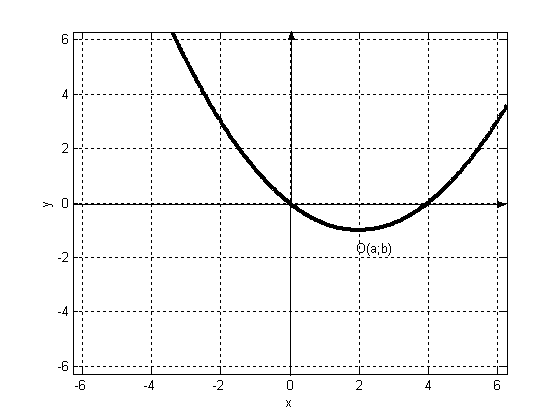
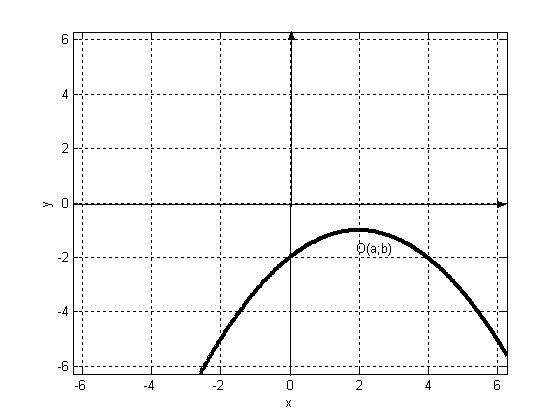
Составить уравнение параболы ______________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
Составить уравнение параболы, ______________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
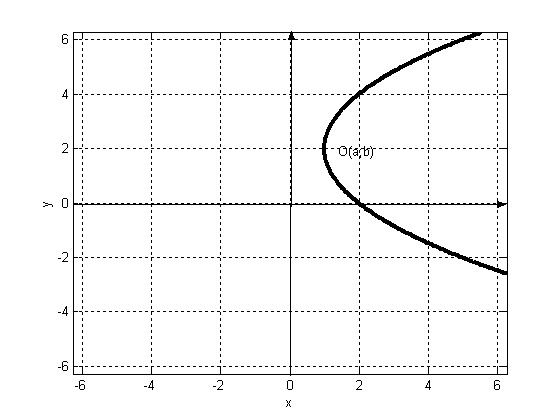
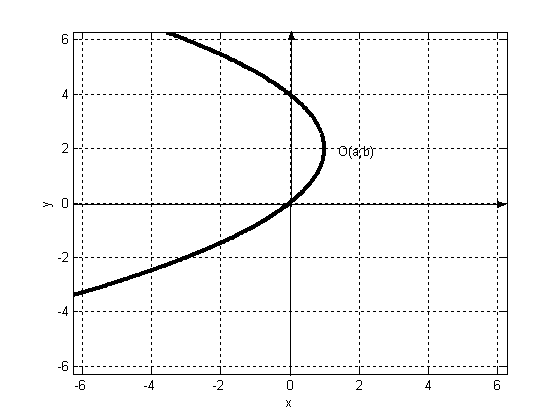
Составить уравнение параболы, ______________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
Допуск к работе
2.2.1 Запишите уравнение эллипса, если его полуоси а = 12, b = 5
__________________________________________________________________________
2.2.2 Запишите уравнение гиперболы , если его полуоси а = 12, b = 5
__________________________________________________________________________
2.2.3 Запишите на какой оси находятся фокусы эллипса, заданного уравнением:
А)
![]() __на оси ______________
__на оси ______________
Б)
![]() __на оси ______________
__на оси ______________
В)
![]() __на оси ______________
__на оси ______________
Г)
![]() __на оси ______________
__на оси ______________
2.2.4 По данному уравнению параболы укажите координаты вершины и параметр
А) (х - 12) 2 = 12(у + 3) _____ вершина О( ___________) , параметр р= _______
Б) (у - 12) 2 = -16(х + 3) _____ вершина О( ___________) , параметр р= _______
2.2.5 Запишите формулы для вычисления с
-
фокусы на оси ОХ
фокусы на оси ОХ
эллипс
гипербола
2.2.6 Запишите
формулы для вычисления
![]()
-
фокусы на оси ОХ
фокусы на оси ОХ
эллипс
гипербола
2.2.7 Запишите уравнение окружности с центром в точке O (-3;2) и радиусом r = 9
__________________________________________________________________________
2.2.8 Укажите координаты центра и радиус окружности, заданной уравнением:
(х - 8)2 + (у + 5)2 = 64 центр О( ___________) , радиус r = _______
К работе допускается ______________
ПРАКТИЧЕСКАЯ РАБОТА 7
Расчёт параметров кривых второго порядка с помощью MathCAD.
Цель работы
Научиться находить с помощью пакета MathCAD параметры кривых второго порядка
Научиться строить с помощью пакета MathCAD кривые второго порядка
Оборудование
Пакет программ MathCAD.
Ход работы
3.1. Вариант
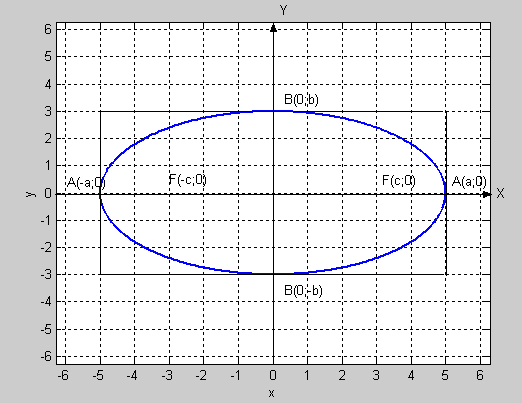
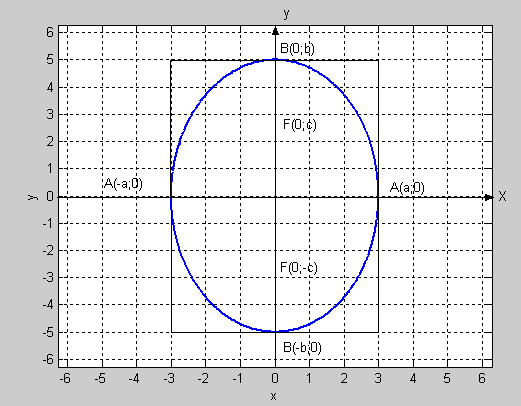
3.1.1 Эллипс задан уравнением
А)
Б)
Найти a, b, c, ε, координаты точек F1, F2, A1, A2, B1,B2. Выполнить чертёж.
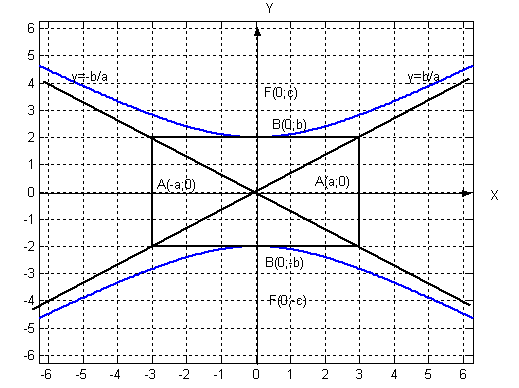
3.1.2 Гипербола задана уравнением
А)
Б)
Найти a, b, c, ε, координаты точек F1, F2, координаты вершин, уравнение асимптот. Выполнить чертёж.
3.1.3 Найти вершину, фокус, параметр и уравнение директрисы параболы Выполнить чертёж.
А)
Б)
Допуск к работе
3.2.1 Заполните пропуски:
Соотношение между а и b |
a □ b |
a □ b |
Расположение эллипса относительно осей координат |
Эллипс вытянут вдоль оси О □ |
Эллипс вытянут вдоль оси О □ |
Рисунок |
эллипс вписан в прямоугольник со сторонами 2а и 2 b |
|
Положение фокусов |
F1, F2 O □ |
F1, F2 O □ |
Координаты фокусов |
F1( □;□), F2( □; □ ) |
F1( □;□), F2( □; □ ) |
Фокусное расстояние |
| F1F2 | = 2с |
| F1F2 | = 2с |
Большая ось |
| А1А2 |=2□ |
| В1В2 |=□ b |
Малая ось |
| В1В2 |=□b |
| А1А2 |=2 □ |
Эксцентриситет |
|
|
Соотношение между а, b и с |
□2= a2 □ b2 |
c2 = b2 □ □2 |
Уравнение |
|
|
3.2.2 Заполните пропуски
Положение фокусов |
F1, F2 O□ |
F1, F2 O□ |
Расположение гиперболы относительно осей координат |
Вершины находятся на оси ОХ. Ветви гиперболы расположены слева и справа от прямоугольника со сторонами 2а и 2 b и постепенно приближаются к продолжением его диагоналей (асимптотам гиперболы) |
Вершины находятся на оси ОУ. Ветви гиперболы расположены слева и справа от прямоугольника со сторонами 2а и 2 b и постепенно приближаются к продолжением его диагоналей (асимптотам гиперболы) |
Рисунок |
|
|
Координаты вершин |
А1( □;□), А2( □; □ ) |
В1( □;□), В2( □; □ ) |
Координаты фокусов |
F1( □;□), F2( □; □ ) |
F1( □;□), F2( □; □ ) |
Фокусное расстояние |
| F1F2 |=2 □ |
| F1F2 |=2 □ |
Действительная ось |
| □ □ | = 2 □ |
| В1В2 |=2□ |
Мнимая ось |
| В1В2 |= □ b |
| А1□ | = □а |
Эксцентриситет |
|
|
Соотношение между а, b и с |
c2 = a2 □ b2 |
c2 = □2 + a2 |
Уравнение асимптот |
|
|
Уравнение |
|
|
3.2.3 Заполните пропуски:
|
Рисунок |
Уравнение |
|
Ветви направлены
__________________ |
|
(x - □)2 = 2p( y - b) |
|
Ветви направлены вниз |
|
(x-a)2 = □ 2p(y-b) |
|
Ветви направлены _________________ |
|
(y-b)2 = 2p(x-□) |
|
Ветви направлены влево |
|
(y-b)2 = -2□ (x-a) |
|
К работе допускается ______________
Результаты работы
4.1
А)
a |
b |
c |
ε |
F1 |
F2 |
A1 |
A2 |
B1 |
B2 |
|
|
|
|
|
|
|
|
|
|
Б)
a |
b |
c |
ε |
F1 |
F2 |
A1 |
A2 |
B1 |
B2 |
|
|
|
|
|
|
|
|
|
|
4.2
А)
a |
b |
c |
ε |
F1 |
F2 |
1 |
2 |
асимптоты |
|
|
|
|
|
|
|
|
|
Б)
a |
b |
c |
ε |
F1 |
F2 |
1 |
2 |
асимптоты |
|
|
|
|
|
|
|
|
|
4.3
А)
-
вершина
фокус
параметр
директриса
Б)
-
вершина
фокус
параметр
директриса
5. Вывод
В ходе выполнения данной работы ________________________________________________________________________________________________________________________________________________________________________________________________________________________
ПРАКТИЧЕСКАЯ РАБОТА 8
Применение производной.
Цель работы
Научиться применять производную для решения физических и геометрических задач .
Ход работы
Вариант
Тело массой кг движется по закону
 (S
в метрах, t
в секундах). Найти силу, действующую на
тело и его кинетическую энергию через
с
от начала движения.
(S
в метрах, t
в секундах). Найти силу, действующую на
тело и его кинетическую энергию через
с
от начала движения.
Найти приближенное значение функции
 при х = .
при х = .
Вычислить приближенное значение:
а) б) в)
Зависимость между количеством х вещества, получаемого в некоторой химической реакции, и временем t выражается уравнением x = A(1 + e - kt) , где А – начальное количество вещества. Определите скорость химической реакции в зависимости от наличия действующего вещества, если
А = , k = , t =
х |
-1,5 |
-1,4 |
-1,3 |
-1,2 |
-1,1 |
-1 |
-0,9 |
-0,8 |
ех |
0,223 |
0,247 |
0,273 |
0,301 |
0,333 |
0,368 |
0,407 |
0,449 |
х |
-0,7 |
-0,6 |
-0,5 |
-0,4 |
-0,3 |
-0,2 |
-0,1 |
ех |
0,497 |
0,549 |
0,607 |
0,67 |
0,741 |
0,819 |
0,905 |
Составьте уравнение касательной и нормали к кривой
 в ее точке с абсциссой х0
= .
в ее точке с абсциссой х0
= .
Найти наибольшее и наименьшее значения функции
y
=
на отрезке
![]()
Исследовать функцию и построить её график

2.2. Допуск к работе
2.2.1 Заполните таблицу производных:
|
|
2.2.2 Заполните пропуски
А) Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке _____________________.
Б) Если производная дифференцированной функции _________________ на промежутке, то функция на этом промежутке убывает.
2.2.3 Дорисуйте схемы
А )
Б)
)
Б)

2.2.4 Заполните пропуски:
Пусть материальная точка движется прямолинейно по закону S=S(t), тогда
Скорость прямолинейного движения материальной точки в момент времени t равно ____________ производной от пути по времени.
![]()
_______________ прямолинейного движения материальной точки в момент времени t равно первой производной от скорости по времени или _____________ производной от пути по времени
![]()
2.2.5 Заполните пропуски:
Алгоритм составления уравнения касательной и нормали
Обозначьте абсциссу точки касания х0.
Вычислите □ .
Найдите
 и
вычислите □ .
и
вычислите □ .
Найденные значения х0, f(х0),
 подставьте в уравнение касательной и
нормали.
подставьте в уравнение касательной и
нормали.
Уравнение касательной к графику функции у=f(х) в точке с абсциссой х0 имеет вид:
_________________________________________________
Уравнение нормали к графику функции у=f(х) в точке с абсциссой х0 имеет вид:
____________________________________________
Выполните упрощение, полученных уравнений
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 9
Частные производные
.
Цель работы
Научиться находить частные производные функции двух переменных
Научиться находить локальные экстремумы функции двух переменных.
Ход работы
Вариант
Найти
частные производные
![]() и
и
![]() функции
функции
![]() .
.
z = ________________________
z = ________________________
Найти полный дифференциал функции z = ______________________;
Вычислить значения частных производных
 для данной функции
для данной функции
 в точке
в точке
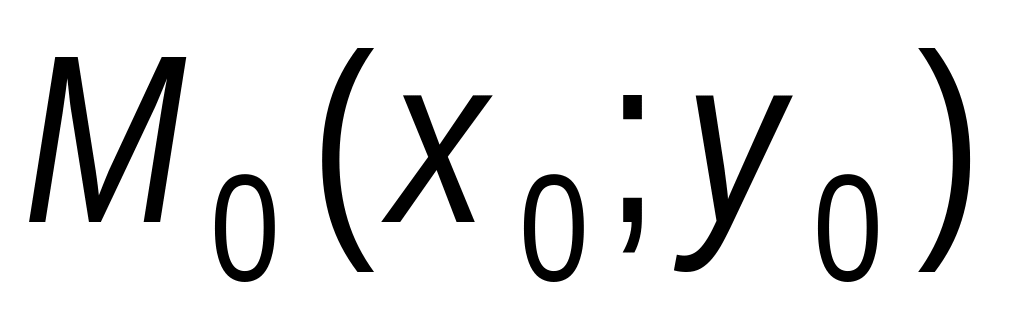 :
:
f (x,y) = ____________________________ , M0( ____ ; ___ );
Найти частные производные
 и
и
 функции
функции
 .
.
z = ________________________
Найти
вторые частные производные
![]() указанной функции. Убедиться в том, что
указанной функции. Убедиться в том, что
![]() .
.
z = ________________________
z = ________________________
Исследовать на экстремум функцию z = ________________________
Проверить, удовлетворяет ли указанному уравнению данная функция U.
____________________________________________________________________
2.2. Допуск к работе
Заполните пропуски:
А) При вычислении z’x , считают, что х – это __________ , а у – постоянная (число).
Б) При вычислении z’у , считают, считают, что х – это постоянная (число),
а у – ____________________
Заполните таблицу
|
|
|
ln( 5x-8y) |
|
|
|
|
|
(2х+3у)соs(4x+12y) Воспользуйтесь правилом вычисления производной произведения (uv)’=u ’ v + u v ’ |
|
|
Воспользуйтесь правилом вычисления производной частного
|
|
|
Вычислить значение функции
 в точке M0(2;-1)
в точке M0(2;-1)
___________________________________________________________
Заполните таблицу:
|
|
|
|
|
|
|
|
Заполните таблицу:
|
|
|
|
|
|
|
8x3y5 |
|
|
|
|
|
|
sin(3x+12y) |
|
|
|
|
|
|
cos(7x-17y) |
|
|
|
|
|
|
e 4x+5y |
|
|
|
|
|
|
Запишите формулу для вычисления полного дифференциала функции двух переменных
_____________________________________________________________________________
Сформулируйте необходимое условие экстремума функции нескольких переменных
____________________________________________________________________________________________________________
Как находят r, s, t, ∆ для проверки достаточного условия экстремума функции двух переменных?
_____________________________________________________________________________
Какими должны быть r и ∆, чтобы точка была точкой минимума?
_____________________________________________________________________________
Каким должно быть ∆, чтобы точка не являлась точкой экстремума?
_____________________________________________________________________________
К работе допускается ______________
3. Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 10
Решение задач дифференциального исчисления
в MathCAD.
Цель работы
Научиться находить с помощью пакета MathCAD производные первого
и второго порядков функций одной и нескольких переменных.
Научиться применять производную для решения геометрических
физических задач с помощью пакета MathCAD.
Оборудование
Пакет программ MathCAD.
Ход работы
3.1 Вариант
1. Найти производную первого порядка

 эллипс
вписан в прямоугольник со сторонами
2а и 2 b
эллипс
вписан в прямоугольник со сторонами
2а и 2 b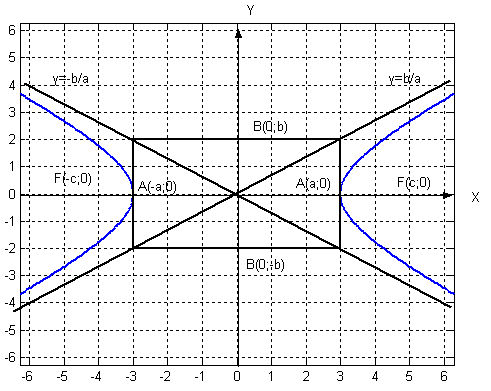
 Направление
ветвей
Направление
ветвей