Министерство образования и науки Российской Федерации

Уральский Федеральный университет

имени первого Президента России Б. Н. Ельцина

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Сборник задач

Екатеринбург

УрФУ

2013

УДК

Составители: Т. И. Кириллова, Л. Ю. Елькина, Л. Ю. Стриганова,

Л. В. Соловьева-Гоголева

Научный редактор доц., канд. техн. наук Н. Х. Понетаева

Выражаем благодарность доц. канд. техн. наук С. В. Арзамасцеву за помощь в подготовке пособия.

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ: метод. пособие / сост. Т. И. Кириллова, Л. Ю. Елькина, Л. Ю. Стриганова, Л. В. Соловьева-Гоголева. Екатеринбург : УрФУ, 2013, 34 с.

Сборник задач по начертательной геометрии является частью учебно-методического комплекса по дисциплине "Инженерная графика" и состоит из 10 тем дисциплины. К каждой теме даются типовые задачи, которые решаются в аудиторное время и студентом самостоятельно. Сборник предназначен, в основном, для студентов обучающихся по направлению 270800.62 − «Строительство», 271101.65 – «Строительство уникальных зданий и сооружений» и может быть использован для других направлений подготовки.

Библиогр. : Рис. 39, назв. 6.

Подготовлено кафедрой «Инженерная графика»

© УрФУ, 2013

СОДЕРЖАНИЕ

Введение ........................................................................................................4
1. Инвариантные свойства ортогонального проецирования ....................5
2. Прямые общего положения. Способ прямоугольного треугольника ..8
3. Плоскость………………..........................................................................10
4. Построение фигур в плоскости, заданной следами. Построение фигур с использованием особых линий плоскости....................................... .12
5. Относительное положение прямой и плоскости, плоскостей ............13 5.1. Пересекающиеся прямая и плоскость, плоскости…………….13 5.2. Параллельные и перпендикулярные прямая и плоскость……15
6. Поверхности. Задание и изображение на ортогональном чертеже.....17
7. Относительное положение поверхности и плоскости .........................18
8. Относительное положение поверхностей.............................................24
9. Способы преобразования проекций…………......................................29 10. Построение проекций поверхностей по заданным условиям……...31

Введение

Сборник задач предназначен для решения задач на практических занятиях по начертательной геометрии и самостоятельной работы студентов, для подготовки к проверочным работам, зачету или экзамену.

При решении задач все построения и надписи выполняют простым мягким карандашом марки М, B, F или HB с применением чертёжных инструментов (линейки, циркуля, транспортира), в тетради в клетку.

Если в условии задачи указан метод решения, то задачу нужно решать указанным методом. Если задача задана рисунком, то условие нужно перечертить в тетрадь в соответствии с указанными размерами.

Задачи раздела 1, 2, 3, 4, 5, 9, 10 решаются в системе двух плоскостей проекций: горизонтальной П₁ и фронтальной П₂. Профильная проекция строится, если это указано в условии задачи.

Задачи раздела 6, 7, 8 решаются, в основном, в системе трех плоскостей проекций. В задачах, где используются поверхности, обязательно определять видимость поверхностей. Невидимые линии вычерчивать штриховой линией (длина штриха 4-5 мм, пробел 1-2 мм). Проекции осей и центровых линий в окружности выполнять штрихпунктирной линией (штрих 10-15 мм, пробел 2 мм, пунктир 1-2 мм, пробел 2 мм).

Все вспомогательные построения выполнять тонкими линиями твёрдым карандашом и не удалять с чертежа.

Все задачи решают графически, без математических вычислений.

1. Инвариантные свойства ортогонального проецирования

Инвариантные свойства – это свойства как данного объекта, так и его ортогональных проекций.

1. Проекция точки есть точка: А → А₁, А → А₂.

2. Проекции точек лежащих на проецирующем луче совпадают: АВ  П₁ => А₁≡ В₁.

3. Точка, принадлежащая прямой, проецируется в точку принадлежащую проекции этой прямой: С  АВ => С₂  А₂В₂.

4. Проекции точек расположенных в плоскостях проекций, совпадают с самой точкой: С є П₁ => С ≡ С₁, D є П₃ => D ≡ D₃.

5. Проекция прямой есть прямая: СD → C₁D₁; СD → C₂D₂, исключение представляют прямые перпендикулярные плоскостям проекций.

6. Проекции параллельных прямых параллельны

a ‖ b => a₁ ‖ b₁ => a₂ ‖ b₂.

7. Отношение длин отрезков прямой или параллельных отрезков равно отношению их проекций.

8. Отрезок прямой, параллельный плоскости проекций, проецируется на нее в натуральную величину АВ II П₂ => А₂В₂ II АВ, IАВI = IА₂В₂I.

9. Проекции пересекающихся прямых имеют одну общую точку, проекции точки пересечения проекций лежат на одной линии связи.

10. Проекция многоугольника есть многоугольник.

11. Прямой угол, у которого одна сторона параллельна плоскости проекций, проецируется на эту плоскость в натуральную величину.

Задача 1.1. Построить три проекции точек заданных координатами и оп-ределить их положение в пространстве.

А (60, 40, 35); В (50, 20, 0); C (40, 0, 25); D (20, 0, 0).

Задача 1.2. Построить фронтальную и горизонтальную проекции прямых AB и СD. Прямая AB││П₁, │AB│= 40 мм, ψ_АВ = 45°, А (60, 10, 25), X_A ˃ X_B; СD││П₂, │CD│= 25 мм, φ_CD = 30°, С (10, 20, 15), Xc ˂ X_D.

Задача 1. 3. Построить проекции точек E и F, принадлежащих отрезку прямой MN. Точка Е удалена на расстояние 35 мм от плоскости проекций П₁, а точка F – на расстояние 15 мм от плоскости проекций П₂.

M (70, 40, 45); N (20, 5, 15).

Задача 1.4. Построить проекции горизонтального и фронтального следов прямой, проходящей через точки A и B. Определить принадлежность точки М заданной прямой АВ. А (50, 25, 10); В (25, 10, 35); М (?, 15, 10).

Задача 1.5. Достроить проекции параллелограмма ABCD (рис. 1).

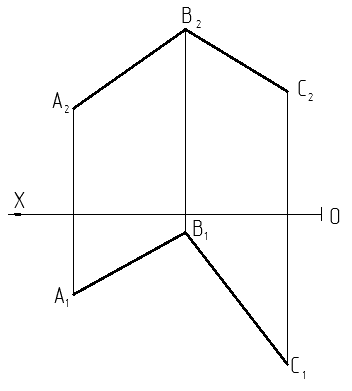
Рис. 1

Задача 1.6. Построить прямой угол ABC, у которого сторона ВС принадлежит прямой MN. │BC│= 15 мм (см. рис. 2).

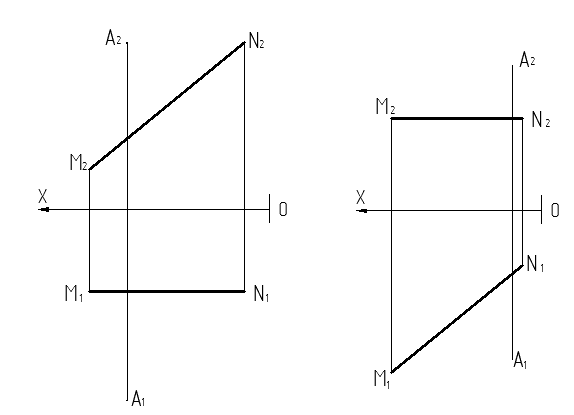
Рис. 2

Задача 1.7. Построить проекции прямой m, пересекающей прямые AB и CD и параллельной оси ОХ. A (45, 50, 10); B (45, 10, 45); C (10, 20, 15); D (35, 35, 35).

Задача 1.8. Построить проекции скрещивающихся прямых l и m, если точки 1 и 3, принадлежат прямой l, а точки 2 и 4 прямой m (рис. 3).

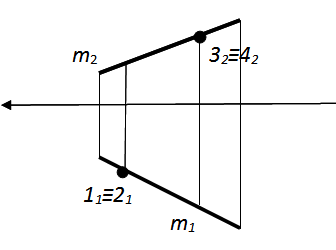
Рис. 3