Раздел 3. Дифференциал функции.

3.1. Общие понятия.

Дифференциал функции выводится из определения производной: . Следовательно, , где β – бесконечно малое число. Отсюда можно найти ∆у: . Последнее слагаемое в этом выражении имеет второй порядок малости, поэтому первое слагаемое главным образом и определяет величину приращения функции и поэтому называется главной линейной частью приращения функции или ее дифференциалом и обозначается dy: .

Таким образом, дифференциал функции – это главная линейная часть приращения функции.

Погрешность этого приближенного равенства тем меньше, чем меньше приращение аргумента. Малое значение приращения аргумента принято обозначать dx и называть дифференциалом аргумента функции dx=∆х. Используя данное обозначение, можно записать формулу нахождения дифференциала функции, зависящего от одного аргумента: .

Свойства дифференциала функции.

1. Дифференциал постоянной величины равен нулю: , где С – постоянная величина.

2. Постоянный множитель (С) можно выносить за знак дифференциала: .

3. Дифференциал суммы (разности) равен сумме (разности) дифференциалов: .

4. Дифференциал произведения равен сумме произведений дифференциала первого сомножителя на второй и дифференциала второго сомножителя на первый: .

5. Дифференциал дроби равен: .

6. Дифференциал сложной функции находится по формуле: .

3.2. Нахождение дифференциала функций одной переменной.

Дифференциал функции одной переменной можно находить двумя способами:

1. Вычислить производную функции , а потом ее умножить на дифференциал аргумента : .

2. Использовать свойства дифференциала.

Пример 1. Найти дифференциал функции

Решение 1 способом:

Надо найти дифференциал от произведения функций и . Сначала находим производную функции:

и, умножая ее на dx, получаем дифференциал

Решение 2 способом:

Используем формулу для дифференциала от произведения функции и .

Пример 2. Найти дифференциал функции

Эта функция является сложной, т.е. , где

Решение 1 способом:

Находим производную

Умножив ее на dx, получим дифференциал

Решение 2 способом:

Используем формулу для дифференциала от сложной функции:

.

3.3. Геометрический смысл дифференциала.

Л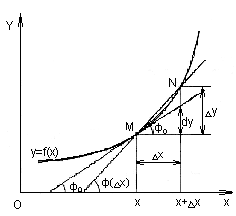 учше всего геометрический смысл дифференциала пояснить, используя рисунок.

Дифференциал функции у=f(x) в точке с абсциссой х равен приращению ординаты касательной, проведенной к графику функции в этой точке, при переходе из данной точки в точку с абсциссой (х+∆х).

Дифференциал может быть как больше, так и меньше приращения функции. Он меньше приращения для вогнутых функций (см. рисунок) и больше для выпуклых функций.

Можно говорить о том, что дифференциал функции имеет и механический смысл. Каков же механический смысл дифференциала?

Если s=f(t) есть путь, пройденный материальной точкой за время t, то, как известно, ds/dt есть скорость движения в момент времени t. Тогда дифференциал пути , то есть приближенно равен пути, пройденному материальной точкой от момента времени t, до момента времени t+∆t, если пренебречь изменением скорости движения на этом промежутке времени.