1.5. Способы задания функции.

1. Табличный способ задания функции.

При этом способе выписываются в определенном порядке значения аргумента и соответствующие значения функции.

х	х1	х2	…	Хn
y	Y1	Y2	…	yn

Примером таких таблиц могут служить таблицы тригонометрических функций, таблицы логарифмов, результаты экспериментов.

2. Графический способ задания функции.

Если в прямоугольной системе координат на плоскости изобразить в виде линии некоторую совокупность точек так, что , где x – абсциссы точек, а y – ординаты, то такая совокупность точек называется графиком функции (рис. 1).

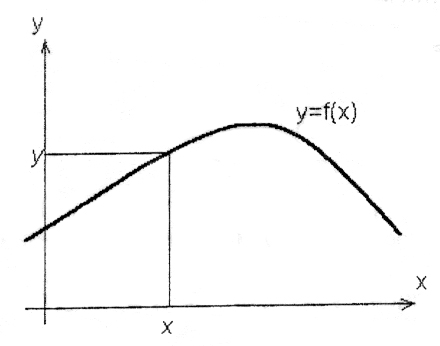
Рис. 1.

Откладывая на оси абсцисс необходимое значение x и восстанавливая перпендикуляр из точки x до пересечения с кривой, а затем, проводя прямую, параллельную оси абсцисс до пересечения ее с осью ординат, получим значение функции в точке x.

3. Аналитический способ задания функции.

При аналитическом способе задания функция представляется аналитическим выражением, то есть через совокупность известных математических операций, которые производятся в определенной последовательности над числами и символами, обозначающими постоянные и переменные величины.

Примером аналитических выражений могут служить: , .

1.6. Элементарные функции. Свойства функций.

К основным элементарным функциям относятся:

1. Степенная функция: , где a – действительное число.

2. Показательная функция: 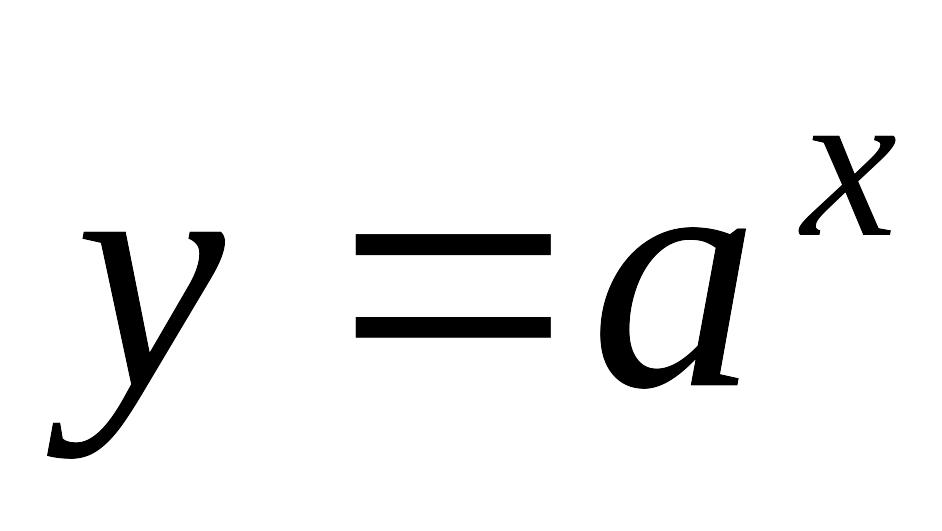, где а – положительное число не равное единице.

3. Логарифмическая функция: 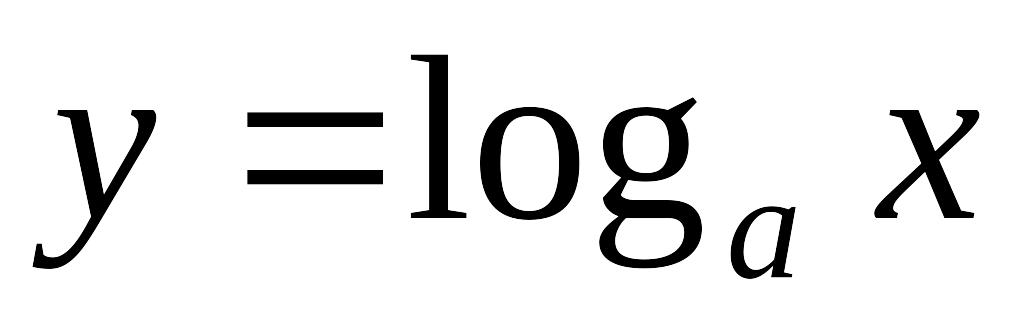, где а – основание логарифма – положительное число, не равное единице.

4. Тригонометрические функции: , , , .

5. Обратные тригонометрические функции: , , , .

Кроме основных элементарных функций к элементарным относятся функции, полученные из последних путем конечного числа операций сложения, вычитания, умножения и деления функции на функцию, а также взятия функции от функции (или сложные функции): .

Вспомним область определения и графики основных элементарных функций:

Степенная функция. .

а) а – целое положительное число. Область определения (-∞, ∞).

Примерный вид функции на рис.2 и рис.3.

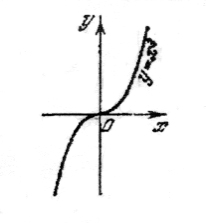
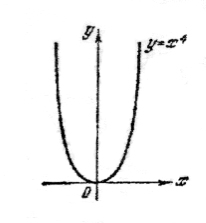
Рис.2. Рис.3.

б) а – целое отрицательное число. Функция определена для всех х за исключением т. х=0. Примерный вид функции показан на рис.4 и рис.5.

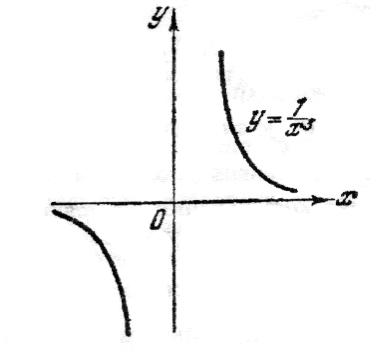
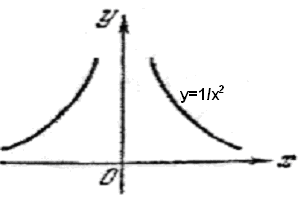
Рис.4. Рис.5.

Приведем также примеры степенных функций при дробно-рациональных значениях а (рис. 6,7,8).

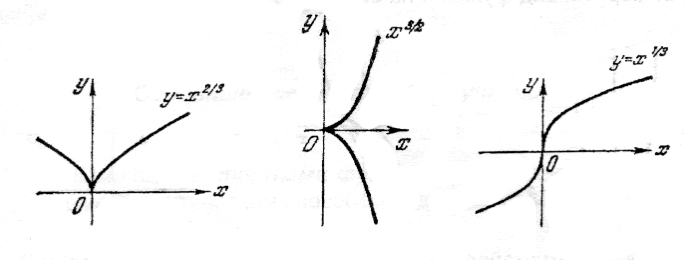
Рис.6. Рис.7. Рис.8.

Показательная функция: ; а>0 и а ≠ 1.

Она определена при всех значениях х. Пример функции показан на рис.9.

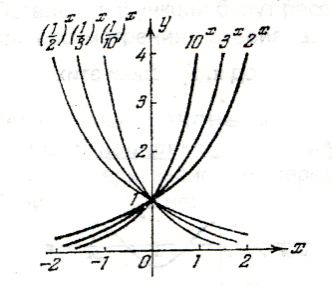
Рис.9.

Логарифмическая функция: ; а>0 и а≠1.

Область определения функции (0, ∞). График функции показан на рис.10.

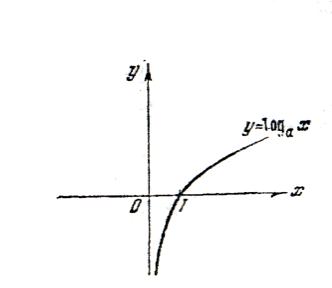
Рис.10.

Тригонометрические функции.

Графики этих функций показаны на рис. 11, 12, 13, 14.

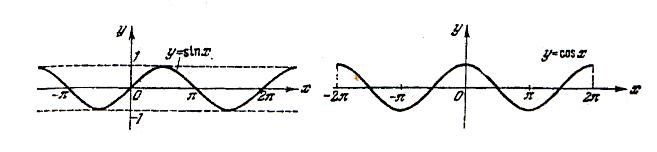
Рис.11. Рис.12.

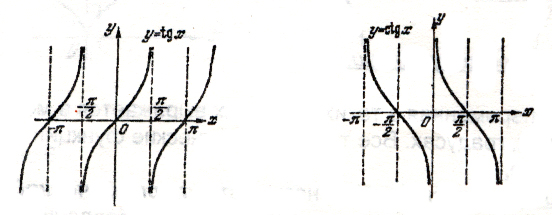
Рис. 13. Рис.14.

Функции и определены для всех х. Функция определена везде, кроме точек , (k=0; ±1; ±2…). Функция также определена везде, кроме точек , (k=0; ±1; ±2…).

Исходя из графиков, мы видим, что функции бывают периодические и непериодические.

Определение: Функция , называется периодической, если существует такое постоянное число Т, при прибавлении или вычитании которого от аргумента значение функции не изменятся, т.е.

, .

Наименьшее такое число Т называется периодом функции.

Все тригонометрические функции – периодические. Непосредственно из определения следует, что функции , – периодические с периодом . Функции и имеют период .

Функции бывают возрастающие и убывающие.

Определение: Функция называется возрастающей в интервале, если большему значению аргумента из этого интервала соответствует большее значение функции, то есть при ∆Х>0 приращение функции ∆У>0.

Функция называется убывающей в интервале, если большему значению аргумента из этого интервала соответствует меньшее значение функции, то есть при ∆Х>0 приращение функции ∆У<0.