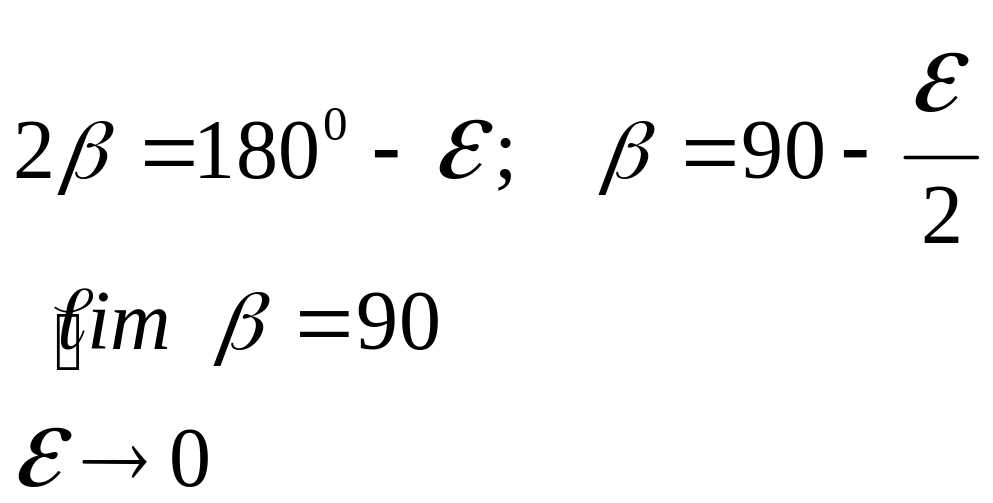3. Определение скорости и ускорения точки при координатном способе задания движения

ТЕОРЕМА: Проекция производной от вектора на какую-нибудь неподвижную ось равна производной от проекции вектора на ту же ось.

.

(1.11)

(1.12)

Если

то (1.13)

Определение скорости точки

Так как, и

но

На основании (1.13), получим

(1.14)

или

Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени.

(1.15)

Система (1.15) определяет модуль и направление вектора скорости точки в пространстве. - углы, которые образует вектор скорости точки с осями координат.

Определение ускорения точки

(1.16)

Следовательно

(1.17)

или

Проекции ускорения на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени.

Модуль и направление ускорения

(1.18)

Где - углы, которые образует вектор полного ускорения точки с осями координат

Движение точки в плоскости

Движение точки по прямой

4. Определение скорости точки при естественном способе задания движения

где

(1.19)

Единичный орт показывает изменение направления вектора скорости точки в случае ее движения по криволинейной траектории

(1.20)

5. Естественные координатные оси

Особенностью данной системы отсчета является то, что начало отсчета всегда находится в точке М и вся система движется вместе с точкой

5. Вектор кривизны кривой в данной точке

(1.21) (1.22) модуль вектора кривизны

(1.23)

Вектор кривизны кривой в данной точке всегда направлен по нормали и модуль вектора обратно пропорционален радиусу кривизны.

6. Определение ускорения точки при естественном способе задания движения

Так как, , то

(1.24)

(1.25)

- нормальное ускорение точки (1.26)

- касательное ускорение точки (1.27)

- полное ускорение точки (1.28)

Частные случаи движения точки

Прямолинейное движение

касательное ускорение характеризует изменение скорости по численной величине

Равномерное криволинейное движение

нормальное ускорение характеризует изменение скорости по направлению

Равнопеременное криволинейное движение

v= v_o + a_ t

Вопросы по теме

КИНЕМАТИКА ТОЧКИ

1. В чем заключается основная задача кинематики?

2. Какие свойства пространства и времени используются в кинематике?

3. Что значит «кинематически задать движение точки»?

4. Перечислите основные способы задания движения точки?

5. В чем заключается векторный способ задания движения точки?

6. В чем заключается координатный способ задания движения точки?

7. В чем заключается векторный способ задания движения точки?

8. Каким уравнением определяется взаимосвязь между векторным и координатным способами задания движения точки?

9. Каким уравнением определяется взаимосвязь между координатным и естественным способами задания движения точки?

10. Как определяется средняя скорость точки при векторном способе задания ее движения? Укажите направление вектора.

11. Как определяется скорость точки в данный момент времени при векторном способе задания ее движения? Укажите направление вектора.

12. Как определяется среднее ускорение точки при векторном способе задания ее движения? Укажите направление вектора.

13. Как определяется ускорение точки в данный момент времени при векторном способе задания ее движения? Укажите направление вектора.

14. Как определяется модуль и направление вектора скорости точки при координатном способе задания ее движения?

15. Как определяется модуль и направление вектора ускорения точки при координатном способе задания ее движения?

16. Запишите выражения для определения вектора скорости точки по модулю и направлению при координатном способе задания ее движения в случае двумерной постановки задачи.

17. Запишите выражения для определения вектора ускорения точки по модулю и направлению при координатном способе задания ее движения в случае двумерной постановки задачи.

18. В чем особенность естественных координатных осей? Как направлены оси естественного трехгранника?

19. Что такое вектор кривизны кривой в данной точке?

20. Как определяется его модуль и направление вектора кривизны кривой в данной точке?

21. Как определяются проекции ускорения точки на естественные координатные оси?

22. Определите физический смысл нормального ускорения точки.

23. Определите физический смысл касательного ускорения точки.

24. Получите закон равнопеременного криволинейного движения в случае, если оно является ускоренным.

25. Получите закон равнопеременного криволинейного движения в случае, если оно является замедленным.

26. Что такое соприкасающаяся плоскость? Какие вектора ускорения точки лежат в этой плоскости?