4.Число вершин і ребер графа

Ступенем вершини в графі (без петель) називається число ребер, інцидентних цій вершині. Наприклад, у графі мал. 4.2 , , , .

Теорема 1. Сума ступенів всіх вершин графа без петель дорівнює подвоєному числу його ребер.

Доведення. Підрахунок числа всіх ребер графа можна вести по вершинах: кількість ребер, інцидентних вершині , дорівнює , вершині – і т.д. При цьому будь-яке ребро враховується двічі (в обох вершинах, яким воно інцидентне).

Теорема 2. Число вершин графа, що мають непарний ступінь, парне.

Доведення. Нехай й – множини всіх вершин графа, що мають парну й, відповідно, непарну ступінь; і – суми ступенів всіх вершин з і з . По теоремі 1, . Тому що числа й парні, то парне. Всі доданки в цій останній сумі непарні, тому їхня кількість повинна бути парною.

Зауваження. Теореми 1 й 2 можна поширити на графи з петлями, якщо при визначенні ступеня вершини кожну інцидентну їй петлю вважати за два ребра.

Визначення. Граф без петель називається однорідним (регулярним) ступеня , якщо всієї його вершини мають ту саму ступінь .

Число ребер такого графа з вершинами дорівнює . Повний граф з вершинами – однорідний ступеня ; число його ребер дорівнює . Нуль-граф - однорідний ступеня 0.

Якщо граф заданий матрицею суміжності або матрицею інциденцій, то ступінь його -й вершини дорівнює сумі елементів його -го рядка. Якщо при цьому граф містить петлі, то залежно від характеру задачі діагональні елементи матриці суміжності повинні входити в суму з коефіцієнтами 1 або 2.

5. Плоскі графи

При зображенні графів на мал. 4.2, 4.4 й ін. ребра графів перетиналися в точках, що не є вершинами графа; щоб виділити вершини, ми зображували їх кружечками.

Визначення. Граф називається правильно укладеним на площині, якщо він зображений на площині так, що його ребра перетинаються тільки в його вершинах.

Визначення. Граф називається плоским (планарным), якщо він ізоморфний деякому графу , правильно укладеному на площині.

Наприклад, граф на мал. 4.4 плоский, тому що він ізоморфний графу на мал. 4.13.

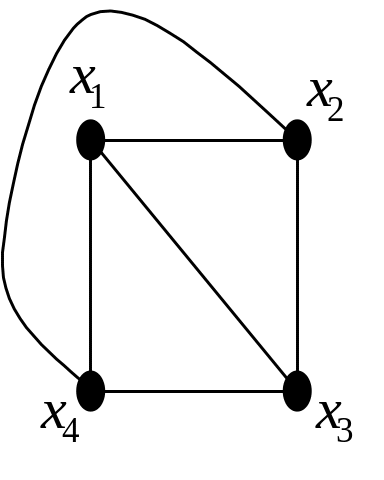
Рис. 4.13

Іншими словами, плоский граф - це граф, який можна правильно укласти на площині.

Задача про можливість правильного укладання графа на площині є досить актуальною у зв'язку з використанням у радіотехніці друкованих схем, які наносяться на основу з ізолятора друкованим способом. Якби при цьому два яких-небудь провідника («ребра» відповідного графа) перетиналися в зайвій точці, не передбаченою схемою (тобто не у вершині графа), то в схемі відбулося б коротке замикання: провідники не ізольовані. Отже, для друкування схем необхідно, щоб її граф був плоским.

У зв'язку із плоскими графами розглянемо наступну задачу. Чи можна побудувати друковану схему, у якій кожний з 3-х полюсів-входів з'єднувався б з кожним з 3-х полюсів-виходів .

В іншій постановці задача виглядає в такий спосіб. Є три міста й три джерела постачання: водонапірна башта , електростанція й станція магістрального газопроводу . Чи можна з'єднати ці міста із джерелами постачання водопроводами, газопроводами й кабелями електропередачі так, щоб траншеї, прориті для цих ліній, не перетиналися?

Ця задача відома як стародавня головоломка про 3-и будинки й 3-и колодязі.

Обидві ці задачі зводяться до побудови плоского графа, ізоморфного графу , показаному на мал. 4.14.

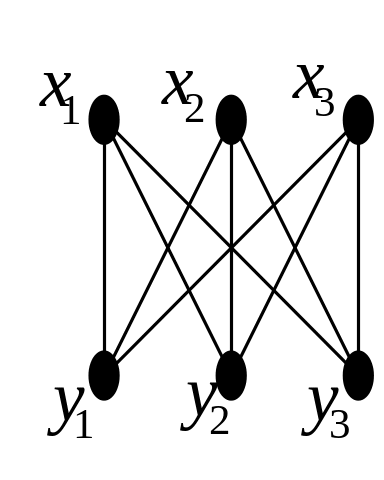
Рис. 4.14

Безпосередні спроби намалювати подібного роду граф приведуть нас до невдачі. Завжди можна намалювати 8 попарно не пересічних ліній, а дев'ята обов'язково перетне одну із цих восьми.

Строгий доказ неможливості такої побудови опирається на теорему, уперше доведену Жорданом.

Теорема.Нехай – безперервна замкнута лінія без само перетинів на площині (див. мал. 4.15).

Рис. 4.15

Вона ділить площину на зовнішню й внутрішню області, що не мають загальних точок. Будь-яка безперервна лінія, що з'єднує дві точки й із внутрішньої й відповідно із зовнішньої області, перетинає .

Доведення. Заміняючи граф (мал. 4.14) йому ізоморфним, приходимо до мал. 4.16.

Рис. 4.16

З'єднання з без перетинання проведених раніше ребер неможливо, тому що точка лежить усередині області, обмеженої кривою , а точка – поза нею.

Точно так само можна показати, що повний граф на мал. 4.17 не є плоским.

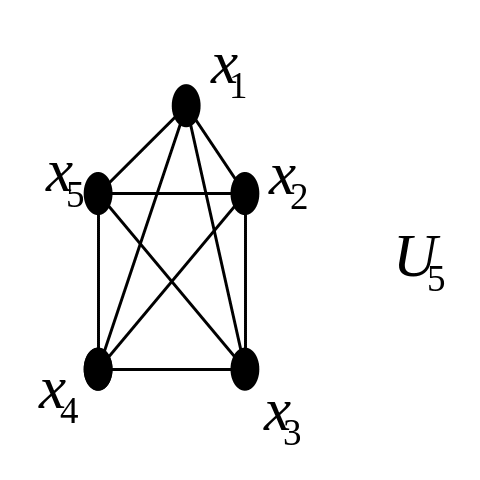
Рис. 4.17

Якщо на ребра графа або помістити довільну кількість додаткових вершин ступеня 2, то, мабуть, знову вийде неплоский граф або відповідно (див. мал. 4.18 й 4.19).

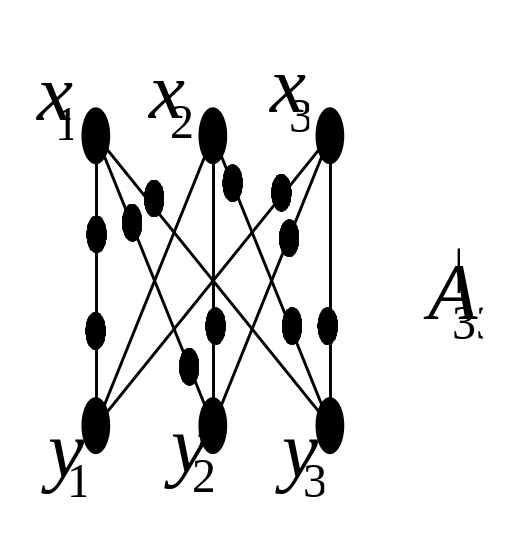
Рис. 4.18 Рис. 4.19

Сформулюємо тепер належний Понтрягину й Куратовскому критерій планарности графів.

Теорема 3. Для того, щоб граф був плоским, необхідно й достатньо, щоб він не містив підграфа, ізоморфного якому-небудь графу й .

Наприклад, граф на мал. 4.12 не плоский, тому що підграф, що залишився після видалення з нього ребер й , ізоморфний графу .

Є й інші критерії планарности, іноді ними користуватися простіше.

170