МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

Лекція 1

Тема: «Основні поняття теорії графів. Ізоморфізм. Матриці суміжності та інцидентності. Плоскі графи.»

Дисципліна: «Дискретна математика»

Викладач: Гусарова І.Г.

Харків 2014

1.Графи. Основні поняття

Дуже часто, бажаючи зрозуміти краще умову задачі, зробити її більше наочної, ми малюємо зазначені в задачі об'єкти у вигляді точок і з'єднуємо ці точки лініями, що означають зв'язки між об'єктами. Такі схеми малюємо в задачах, де мова йде про розподіл води, електроенергії, пари, газу й т.д.. За допомогою подібних схем зображуємо систему зв'язку, розподілу інформації, економічні зв'язки між підприємствами, послідовність виконання операцій і т.д. Коло питань, де використовуються подібні схеми, надзвичайно широка. Тому становить інтерес спеціальне вивчення властивостей таких схем, незалежно від того, у якій конкретно інженерній, економічній, фізичній задачі вони виникли. Цими питаннями займається теорія графів.

Визначення. Графом називається схема, що складається з деякої множини точок, які називаються вершинами, і з'єднуючих їх ліній, які називаються ребрами.

Приклади графів:

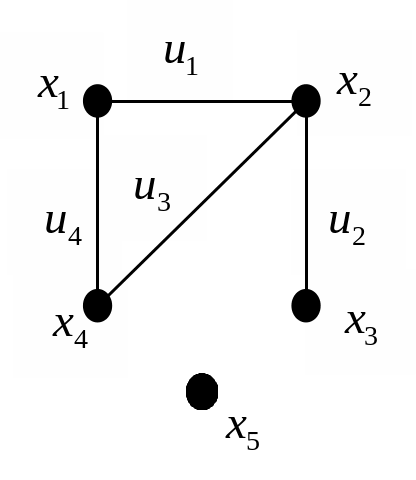
Рис. 4.1 Рис. 4.2

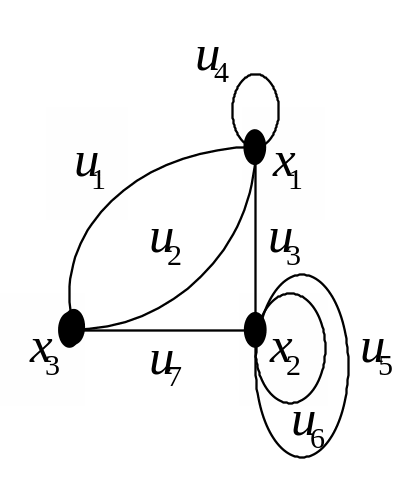
Рис. 4.3

Граф із множиною вершин і множиною ребер часто позначається через . Усюди надалі множини й передбачаються скінченими.

На кресленні ребра графа зображуються відрізками прямих, а якщо або це неможливо або незручно, то лініями простої форми (і у всякому разі без самоперетинів ). Точки перетинання ребер графа не обов'язково є його вершинами. Звичайно вершини графа серед інших точок, утворених перетинанням його ребер, виділяють досить чітко, наприклад, кружечками.

Визначення. Вершина графа називається ізольованої, якщо вона не з'єднана ребром з жодною іншою вершиною графа.

На малюнку 4.1 вершина – ізольована.

Визначення. Граф , що складається з ізольованих вершин (і не утримуючий інших вершин), називається нуль-графом або нульовим графом.

Діаграми Ферре є нуль-графами. Кожна неізольована вершина графа служить кінцем для одного або декількох ребер. Всі ці ребра називаються інцидентними вершині .

Ребро, що з'єднує вершини й , позначається через .

Визначення. Дві вершини, з'єднані ребром, називаються суміжними. Два ребра, що мають загальну вершину, також називаються суміжними.

Визначення. Вершина, яка інцидентна тільки одному ребру, називається кінцевою, інцидентне їй ребро називається кінцевим.

У графі можуть виявитися пари вершин, з'єднані двома або більше ребрами. Такі ребра виявляються кратними.

Визначення. Ребра , інцидентні тільки одній вершині , називаються петлями.

Іноді під терміном «граф» розуміють граф без петель і кратних ребер. Тоді граф, у якому є кратні ребра, називають мультиграфом, кратні ребра й петлі – псевдографом.

Визначення. Граф без петель і кратних ребер називається повним, якщо будь-яка пара його вершин з'єднана ребром. Повний граф з вершинами позначається через . На малюнку 4.4 показаний граф .

Рис. 4.4

Нехай й – дві графи (без петель і кратних ребер) з тим самим множиною вершин .

Визначення. Граф називається доповненням графа , якщо дві вершини в суміжні тоді й тільки тоді, коли вони не суміжні в . Граф на малюнку 4.5 є доповненням до графа на малюнку 4.1.

Рис. 4.5

При цьому граф є, у свою чергу, доповненням графа , тобто .

Якщо – доповнення графа й , то граф – повний. Доповненням нуль-графа є повний граф .

Визначення. Граф називається підграфом графа , якщо кожна вершина й кожне ребро графа є відповідно вершиною й ребром графа .

Визначення. Остовний підграф – це підграф графа , що містить всі його вершини.

Говорять, що підграф графа породжений множиною вершин , якщо він містить всі ребра графа , що з'єднують вершини з .

Приклад. Граф :

Рис. 4.6

є підграфом графів на малюнках 4.1 й 4.4.

Для графа (мал. 4.1) він породжений множиною вершин , для графа (мал. 4.4) – ні.