10.4.Уравнения Максвелла в дифференциальной форме

Уравнения Максвелла можно представить в дифференциальной форме. Для этого левые части уравнений (1, 2) преобразуем по теореме Стокса и получим:

(1а) (2а)

А левые части уравнений (3,4) преобразуем по теореме Остроградского-Гаусса и получим:

(3а) (4а)

В этой форме уравнения показывают, как связаны между собой характеристики электромагнитного поля и плотности электрических зарядов и токов в каждой точке поля.

Уравнения (1а, 3а) говорят о том, что электрическое поле может возникнуть по двум причинам: из-за наличия электрических зарядов (сторонних и связанных) и, кроме того, поле возникает всегда в пространстве при изменении магнитного поля .

Уравнение (2а) показывает, что магнитное поле возникает либо при движении электрических зарядов (электрическими токами), либо переменными электрическими полями, либо и тем и другим одновременно.

Из уравнения (4а) следует, что источников магнитного поля, подобных электрическому заряду для электрического поля, не существует.

Уравнения Максвелла в дифференциальной форме позволяют вычислять поля и . Совместно с уравнением движения заряженных частиц: эти уравнения составляют фундаментальную систему, достаточную для описания всех электромагнитных явлений.

10.5. Электромагнитная волна

Из уравнений Максвелла следует важнейший вывод о существовании принципиально нового физического явления: эл.магн. поле способно существовать самостоятельно – без электрических зарядов и токов! При этом изменение его состояния обязательно носит волновой характер. Поля эти называют эл.магн. волнами.

Выяснилось, что ток смещения , играет при этом первостепенную роль. Его присутствие наряду с величиной и означает возможность появления эл.магн. волн. Всякое изменение во времени магнитного поля возбуждает электрическое поле; в свою очередь, всякое изменение во времени электрического поля возбуждает магнитное поле. За счет непрерывного взаимопревращения (или взаимодействия) они и должны сохраняться – эл.магн. возмущение будет распространяться в пространстве.

Из школьного курса физики известно уравнение плоской волны, распространяющейся вдоль направления x:

, где - волновое число, а - фазовая скорость волны.

Взяв вторые производные по времени и по координате, получим:

; .

Аналогично, можно найти производные по другим координатам для произвольного направления распространения волны. Сложив производные по координатам, получим:

, где - лапласиан.

Выражая из второй производной по времени: и подставляя в последнее уравнение, найдем:

. Это есть общий вид волнового уравнения.

Покажем, что оно вытекает из уравнений Максвелла. Для этого возьмем однородную нейтральную ( ), непроводящую ( ) среду. В проводящей среде волна гасится из-за индукционного тока. Тогда уравнения запишем в виде:

(1) (3)

(2) (4)

Если взять ротор от обеих частей уравнений (1) и (2) то:

и

Раскрыв левые части по формуле , а в правые части подставив (1) и (2), получим: и .

Заменив , где с - электродинамическая постоянная, найдем, что:

(5) и (6)

Эти уравнения похожи на уравнения волны, если коэффициенты при производных равны , где - фазовая скорость волны, равная в среде:

. Для вакуума - скорости света.

Т.о., доказано, что волновое уравнение непосредственно вытекает из уравнений Максвелла.

Из этих уравнений также следует, что эл.магн. волна является поперечной. Анализ плоской эл.магн. волны в нейтральной , непроводящей среде, вдоль оси x, показывает, что векторы и образуют с направлением распространения волны правовинтовую систему.

На рис.10.4 показана “моментальная” фотография такой эл.магн. волны. В фиксированной точке пространства векторы и изменяются со временем синфазно, а их амплитуды

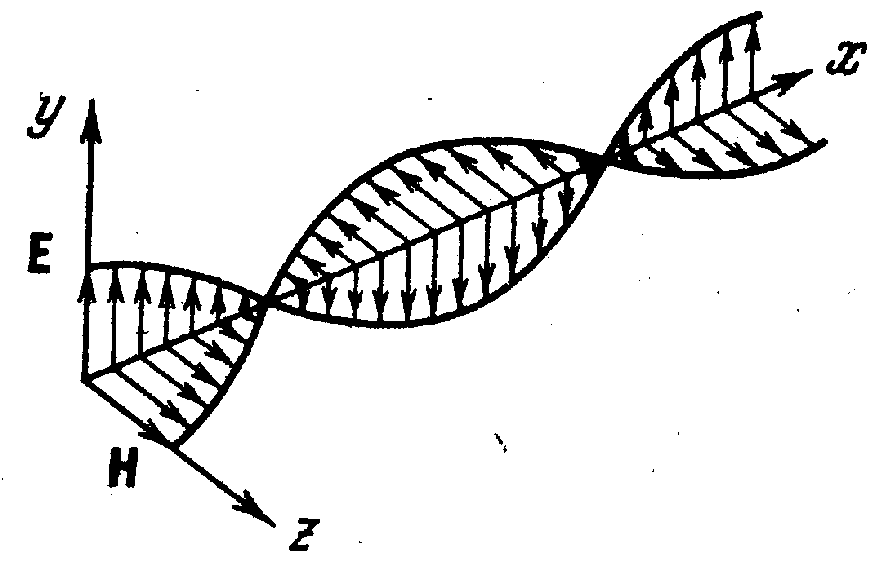
Рис.10.4

связаны соотношением: , в вакууме: 377Ом

Иногда эл.магн. поле представляют в виде сцепленных взаимно-перпендикулярных колец, изображающих силовые линии вихревого электрического и магнитного полей.