13

10. Уравнения Максвелла

10.1 Вихревое электрическое поле

Как известно, в проводящем неподвижном контуре индукционный ток возникает благодаря изменению магнитного потока через этот контур. Наличие тока свидетельствует о появлении в контуре сторонних сил, действующих на носители тока. Эти силы не связаны ни с химическими, ни с тепловыми процессами в проводах. Они не могут быть связаны и с магнитными силами, т.к. магнитные силы работы над зарядами не производят. Остается заключить, что индукционный ток обусловлен электрическим полем, возникающем в проводе. Обозначим это поле , т.к. оно связано с изменением магнитного потока.

Запишем для циркуляции вектора по данному контуру:

.

Подставив э.д.с. из закона Фарадея и поток , получим:

Интеграл берется по произвольной поверхности, опирающейся на контур. Т.к. контур и поверхность неподвижны, то операции дифференцирования по времени и интегрирования по площади можно поменять местами и записать частную производную потока по времени, поскольку в общем случае он зависит и от координат.

или в виде: . (*)

Максвелл предположил, что изменяющееся во времени магнитное поле порождает в пространстве электрическое поле независимо от наличия контура, который позволяет лишь обнаружить это поле.

Поле существенно отличается от электростатического, которое является потенциальным и линии напряженности которого начинаются на положительных и заканчиваются на отрицательных зарядах. Для электростатического поля и в любой точке.

Тот факт, что для электрического поля, возбуждаемого изменяющимся во времени магнитным полем циркуляция и ротор отличны от нуля означает, что это поле не потенциально. Оно, как и магнитное поле является вихревым.

В общем случае, уравнение (*) справедливо, когда присутствуют оба вида поля.

Уравнение (*) является одним из основных в электромагнитной теории Максвелла. Наличие взаимосвязи между электрическим и магнитным полями, выраженное в этом уравнении, является причиной того, что их раздельное рассмотрение имеет лишь относительный смысл. Действительно, электрическое статическое поле создается неподвижными зарядами относительно некоторой инерциальной системы. Однако по отношению к другой инерциальной системе отсчета эти заряды движутся и порождают магнитное поле, которое является вихревым. Неподвижный провод с током создает постоянное магнитное поле в каждой точке пространства. Относительно другой инерциальной системы отсчета этот провод движется и его магнитное поле в конкретной точке пространства меняется и возбуждает вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета является чисто электрическим или чисто магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей, образующих единое электромагнитное поле.

10.2. Ток смещения.

Одной из важнейших новых идей, выдвинутых Максвеллом была идея о симметрии во взаимозависимости электрического и магнитного полей. А именно: если меняющееся во времени магнитное поле создает электрическое поле , то следует ожидать, что изменяющееся во времени электрическое поле создаст магнитное поле. И наиболее существенным шагом на этом пути стало открытие тока смещения.

Понятие тока смещения Максвелл ввел для количественной характеристики “магнитного действия” изменяющегося электрического поля. По теореме Гаусса . Продифференцировав ее по времени получим:

.

Если поверхность S неподвижна и не деформируется, то изменение потока

связано только с изменением вектора D со временем. Значит, полную производную можно заменить на частную и записать:

.

Правая часть имеет размерность тока, а - размерность плотности тока, поэтому Максвелл предложил назвать плотностью тока смещения , тогда величина является током смещения.

Физическую суть тока смещения можно понять, применив теорему о циркуляции вектора к случаю разряда предварительно заряженного конденсатора на некоторое внешнее сопротивление. В качестве контура берем кривую Г, охватывающую провод, рис.10.1. Контур может опираться на разные произвольные поверхности, например S или S. Через поверхность S течет т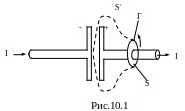 ок разряда , через S, т.е. между обкладками конденсатора, никакого тока нет. Получается, что циркуляция вектора зависит от того, на какую поверхность опирается контур, что явно абсурдно. Для первого случая:

, а для второго - , т.к. ток равен нулю.

Этого можно избежать, если правую часть теоремы несколько изменить. На рис. видно, что поверхность S пронизывает только электрическое поле конденсатора. Для этого поля можно записать теорему Гаусса для замкнутой поверхности, состоящей из S и S. Поток вектора электрического смещения через эту поверхность:

, откуда: .

С другой стороны, из уравнения непрерывности для этой поверхности:

Сложив два последние уравнения, получим:

(**)

По форме это уравнение аналогично уравнению непрерывности для постоянного тока и является условием стационарности. Из него видно, что кроме плотности тока проводимости (в проводах) для выполнения теоремы о циркуляции необходимо еще одно слагаемое - плотность тока смещения. Сумму и называют полным током (плотностью тока): .

Согласно (**) линии полного тока непрерывны в отличие от линий тока проводимости, которые разрываются в конденсаторе. Токи проводимости там замыкаются токами смещения при его заряде и разряде.

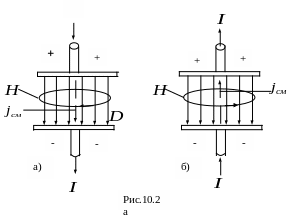
На рис.10.2 а показан конденсатор, который заряжается током проводимости (в проводах). Между обкладками цепь замыкается током смещения , создающим магнитное поле . При заряде конденсатора напряженность поля растет, . При разряде – поле ослабляется, и ток смещения меняет знак (направление).

Введение полного тока устраняет трудность, связанную с зависимостью циркуляции от выбора поверхности, опирающейся на контур Г. Для этого достаточно в правой части уравнения записать полный ток:

.

Это выражение является вторым уравнением Максвелла. Его экспериментальным доказательством служат опыты Эйхенвальда, который изучал магнитное поле токов поляризации.

Ток смещения эквивалентен току проводимости лишь по способности создавать магнитное поле. По существу это есть изменяющееся со временем электрическое поле , а током называется только из-за размерности. Ток смещения не выделяет джоулева тепла.

Поскольку , то видно, что плотность тока смещения складывается из ”истинного” тока смещения в вакууме и тока поляризации , - величины, обусловленной смещением связанных реальных зарядов. В том, что токи поляризации создают магнитное поле нет ничего удивительного, т.к., по своей природе они не отличаются от токов проводимости. Принципиально новое содержится в утверждении, что и другая составляющая тока смещения: , не связанная с движением зарядов, а обусловленная только изменением электрического поля, также создает магнитное поле! Даже в вакууме всякое изменение во времени электрического поля возбуждает в окрестности магнитное поле.

Это открытие Максвелла по своему значению аналогично открытию электромагнитной индукции Фарадея.