Этот материал показывает, насколько «школьная» физика неполна и упрощена по сравнению с более строгой «университетской» физикой.
Часть 2. Элементы термодинамики.
§20. Динамические и термодинамические (статистические) системы.
Рассмотрена механика движения
материальной точки, системы материальных
точек, твердого тела. Динамика этих
систем изучается на основе Второго
закона Ньютона или его обобщений. Было
отмечено, что для решения основной
задачи динамики одной материальной
точки в общем случае надо записать три
уравнения движения (или одно векторное
уравнения, что то же самое) и задать
шесть начальных условий. Обычно указывают
начальные значения координат и скоростей,
.
Если материальных точек
,
надо записать
уравнений движения и
начальных условий. Для двух – трех
частиц основную задачу динамики можно
решить «руками». Для большего числа
частиц возможно численное решение с
использованием компьютера. При этом
исследуются и предсказываются динамические
закономерности движения.
Однако, если рассмотреть некоторый
объем газа, то динамический подход не
пригоден. Действительно, даже в одном
кубическом сантиметре одноатомного
газа при нормальных условиях (некоторые
термины, известные заранее, будут
уточняться позже) содержится так
называемое число Лошмидта, несколько
меньшее, чем
атомов. Очевидно, что невозможно записать
даже уравнения Второго закона для такого
числа материальных точек. А ведь надо
еще указать равнодействующие силы,
действующие на каждую частицу, и указать
в шесть раз большее число начальных
условий. Даже формулировка динамической
задачи в этом случае потребует времени,
сопоставимого с временем существования
Вселенной. А ведь надо еще решить эти
уравнения на ПК, причем с очень малым
шагом по времени (шаг должен быть
значительно меньше, чем время между
последующими соударениями частиц).
В связи со сказанным была развита новая физическая теория движения большого числа частиц. Эта теория принципиально отличается от классической механики. Она состоит из двух «ветвей», термодинамического и статистического методов описания. Принципиальность различия состоит в том, что использование Второго закона Ньютона дает однозначное, предопределенное или детерминированное описание, тогда как термодинамика и статистическая физика рассматривают средние значения физических величин для некоторого числа атомов. Кстати, совокупность этих атомов (или других частиц) называют статистическим ансамблем.
Другое важное отличие связано с характером движения частиц. В классической механике приборами можно отслеживать индивидуальное движение материальных точек. В больших ансамблях (газа, твердого тела, жидкости) происходит скрытое от невооруженного глаза тепловое движение.
§21. Состояние термодинамического ансамбля. Уравнения состояния.
Говоря о материальной точке, мы
отмечали, что её механическое состояние
определяется шестью функциями времени:
.
В термодинамических и статистических
ансамблях тоже используется понятие
состояния. Это так называемые
макроскопические (т.е. характеризующие
всю систему или значительную её часть)
параметры. В простейшем случае это объем
системы
,
давление
и её термодинамическая или абсолютная
температура
.
В системе единиц СИ объем измеряется
в кубических метрах, давление – в
паскалях (
,
нормальное атмосферное давление
составляет
),
температура в кельвинах,
.
Как дополнительный параметр часто
указывают энтропию S,
которую мы определим позже. В некоторых
случаях указывают энтальпию, а также
свободную энергию.
Если удается для какой-то термодинамической модели установить соотношение
,
(как прежде – число частиц в ансамбле), то говорят, что задано уравнение состояния системы.
Единого уравнения состояния не существует. Укажем две модели, лежащие в основе термодинамики.
Модель идеального газа.
Идеальным считается газ из материальных точек, не взаимодействующих друг с другом. Это, например, разреженные одноатомные или молекулярные газы. Это уравнение можно вывести из основных постулатов динамики материальной точки. Оно получило названия «Уравнение состояния идеального газа» или «Уравнение Менделеева – Клайперона»:
или, что то же самое,
.
Здесь
Дж/К – постоянная Больцмана,
Дж/(моль К),
- число молей газа,
1/моль – число частиц в одном моле или
число Авогадро.
Модель газа Ван-дер-Ваальса.
В отличие от идеального газа, модель
Ван-дер-Ваальса лучше соответствует
реальным газам. Она учитывает рассеяние
частиц друг на друге (то есть молекулярные
силы) или внутреннее давление
,
а также собственный объем моля частиц
. Внутреннее давление можно выразить
формулой
,
где
а – константа для данного газа.
Если газ содержит
молей, то уравнение состояния
Ван-дер-Ваальса имеет вид
.
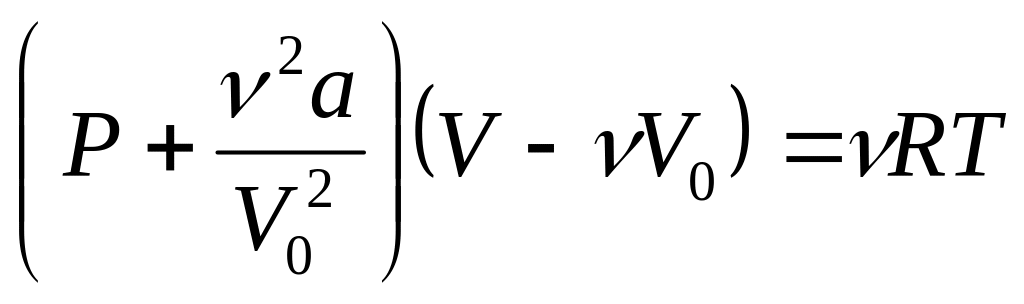Поправки к уравнению идеального газа
должны быть много меньше параметров
.
Указанные примеры относятся к однородным системам, в которых нет переноса массы, импульса и энергии (отсутствие потоков массы, импульса и энергии является условием термодинамического равновесия).
Термодинамическое равновесие – очень интересное состояние системы. Не надо думать, что там вовсе нет потоков энергии, импульса и вещества. Однако эти потоки по всем направлениям одинаковы «как вправо, так и влево», то есть компенсируют друга. Это динамическое равновесие.
Возникновение динамического равновесия является следствием очень давней гипотезы о молекулярном хаосе, согласно которой все направления в пространстве равноправны для термодинамической системы (система изотропна). После небольших преобразований отталкиваясь от идеи молекулярного хаоса можно получить важное соотношение, связывающее температуру ансамбля со средней энергией, приходящейся на одну частицу (атом или материальную точку; для молекул картина несколько сложнее):
.
Отсюда, кстати, следует возможность определения средней скорости частиц:
,
то есть
.
Вектор средней скорости, в силу гипотезы о молекулярном хаосе, равен нулю.
В статистической физике средние значения энергии и скорости получают без гипотезы о молекулярном хаосе.
Если термодинамическое равновесие нарушено и в ансамбле возникли потоки, то говорят, что возникают процессы переноса вещества (диффузия), энергии (теплоперенос, теплопроводность), импульса (внутреннее трение или вязкость). Возможны и другие процессы переноса, в частности, возникновение электрического тока.