Хід заняття

Задача 1. Побудуйте таблиці істинності і доведіть, що наступні формули є тавтологіями:

1. (P®Q) «(ØQ®ØP)

1. (P®Q) ® ((P® (Q® R)) ® (P® R))

Розв’язування.

1) (P®Q) «(ØQ®ØP)

Складемо таблицю істинності даної формули:

Р	Q	PQ	¬Q	¬P	¬Q¬P	(PQ)(¬Q¬P)
0 0 1 1	0 1 0 1	1 1 0 1	1 0 1 0	1 1 0 0	1 1 0 1	1 1 1 1

Таблиця показує, що при всіх можливих розподілах істинносних значень пропозиційних змінних Р і Q, формула завжди набирає значення 1. Тоді, формула – тавтологія.

2) (P®Q) ® ((P® (Q® R)) ® (P® R))

Складемо таблицю істинності даної формули:

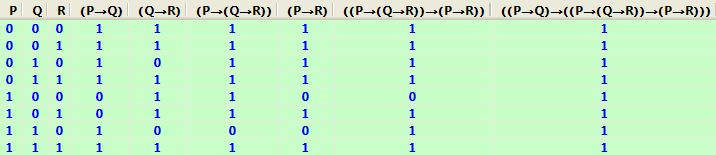
Таблиця показує, що при всіх можливих розподілах істинносних значень пропозиційних змінних Р, Q і R, формула завжди набирає значення 1. Тоді, формула – тавтологія.

Задачі для самостійного розв’язування

2.1 Склавши таблиці істинності, доведіть наступні закони

:

Варіант	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	1,3	2,4	5,21	6,22	7,1	8,10	9,11	12,2	13,11	14,10	15,11	16,21	17,18	19,1	20,22

1. Ø(PÙØP) (закон виключення суперечності)

2. ØØP«P (закон подвійного заперечення)

3. Ø(PÚQ) « (ØPÙØQ) (другий закон де Моргана)

4. Ø(PÙQ) « (ØPÚØQ) (перший закон де Моргана)

5. ((P®Q) Ù (Q®R)) ® (P®R) (правило ланцюгового висновку)

6. ((РÚQ) ÚR) « (PÚ (QÚR)) (комутативність диз’юнкції)

7. ((РÙQ) ÙR) « (PÙ (QÙR)) (асоціативність кон’юнкції)

8. (P Ú (QÙP)) «P (другий закон поглинання)

9. (PÙ (QÚP)) «P (перший закон поглинання)

10. (PÚP) «P (ідемпотентність диз’юнкції )

11. (PÙP) «P (ідемпотентність кон’юнкції)

12. (P«Q) « (ØP«ØQ) (закон протилежності)

13. (P®Q) « (ØPÚQ)

14. (PÚQ) « (ØP®Q)

15. (P«Q) « ((P®Q) Ù (Q®P))

16. (P®Q) « (ØQ®ØP) (закон контрапозиції)

17. (PÚQ) « (QÚP) (комутативність диз’юнкції)

18. (PÙQ) « (QÙP) (комутативність кон’юнкції)

19. (РÚ (QÙR)) « ((PÚQ) Ù (PÚR)) (дистрибутивність диз’юнкції

відносно кон’юнкції)

20. (РÙ (QÚR)) « ((PÙQ) Ú (PÙR)) (дистрибутивність кон’юнкції

відносно диз’юнкції)

21. P®P (закон тотожності)

22. РÚØР (закон виключеного третього)

2.2. Склавши таблиці істинності наступних формул, доведіть, що всі вони є тавтологіями:

1. ((P®Q) Ù (P®ØQ)) ®ØP

2. ((P®Q) ®P) ®P

3. (A® (B® (C® (D® (E® F))))) « ((AÙBÙCÙDÙE) ®F)

4. (A® (B® C)) « ((AÙB) ®C)

5. (P® (Q® R)) ® ((P® Q) ® (P® R))

6. (P® (Q® R)) « (Q® (P® R))

7. (P®Q) ® ((P® (Q® R)) ® (P® R))

8. (P®Q) ® ((P®ØQ) ®ØP)

9. (P®Q) ® ((Q® P) ® (P«Q))

10. (P«Q) ® (P®Q) та (P®Q) Ú (Q®P)

11. ((PÙQ) ® P)® (Q® (PÙQ))

12. (P®R) ® ((PÚQ) ® (RÚQ))

13. (P®R) ®((Q®R) ®((PÚQ) ®R))

14. (Р ® (Q Ù R)) « ((Р® Q) Ù (Р® R))

15. P® (PÚQ) ÙP®(Q® P)

2.3. Виконайте завдання 1.3 з лабораторної 1 за варіантами:

Варіант	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1.3.	6	7	8	9	10	11	12	13	14	15	1	2	3	4	5