Методичні вказівки до виконання контрольної роботи
№1 Для функції, заданої векторно, визначити ДДНФ, ДКНФ, мінімізувати функцію ДДНФ, побудувати КРС по мінімальній формі, записати поліном Жегалкіна (перетворення або метод невизначених коефіціентів)
F={1010 0011}
a |
b |
c |
f |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
ДДНФ:
ДКНФ:
Карта Карно:
bc a |
00 |
01 |
|
10 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
11
1
Результат:
КРС:
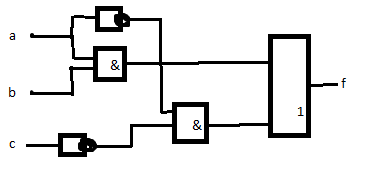
Поліном Жегалкіна:
№2 Перетворити f(X1,X2,X3,X4) використовуючи формули розкладу по сукупності змінних Xn, Xk, представити отримані функції від двох змінних формулами g0,g1,…,g15. Спростити функцію методом Карно
F={1010 1110 0110 0101}, n=1, k=3;
x1 |
x2 |
x3 |
x4 |
f |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
N=1, k=3 x2 |
x4 |
F(0,x2,0,x4) |
F(0,x2,1,x4) |
F(1,x2,0,x4) |
F(1,x2,1,x4) |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
(
Метод Карно:
|
|
|
|
||
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1
1
Результат:
№3 Для булевої функції f, заданої векторно, методом Квайна знайти скорочену ДНФ. Для скороченої ДНФ побудувати матрицю Квайна, указати ядрові імпліканти, знайти мінімальну ДНФ
F={1100 1110 1111 1011}
Index |
|
|
|
|
|
0 |
0000 |
|
|
|
|
1 |
0001 |
0100 |
1000 |
|
|
2 |
0101 |
0110 |
1001 |
1010 |
1100 |
3 |
1011 |
1110 |
|
|
|
4 |
1111 |
|
|
|
|
0-1 |
000* |
0*00 |
*000 |
|
|
|
|
|
1-2 |
0*01 |
*001 |
010* |
01*0 |
*100 |
100* |
10*0 |
1*00 |
2-3 |
*110 |
10*1 |
101* |
11*0 |
|
|
|
|
3-4 |
1*11 |
111* |
|
|
|
|
|
|
0-1-1-2 |
0*0* |
**00 |
|
1-2-2-3 |
*1*0 |
10** |
1**0 |
2-3-3-4 |
1*1* |
|
|
|
0000 |
0001 |
0100 |
1000 |
0101 |
0110 |
1001 |
1010 |
1100 |
1011 |
1110 |
1111 |
0*0* |
x |
x |
x |
|
x |
|
|
|
|
|
|
|
**00 |
x |
|
x |
x |
|
|
|
|
x |
|
|
|
*1*0 |
|
|
x |
|
|
x |
|
|
x |
|
x |
|
10** |
|
|
|
x |
|
|
x |
x |
|
x |
|
|
1**0 |
|
|
|
x |
|
|
|
x |
x |
|
x |
|
1*1* |
|
|
|
|
|
|
|
x |
|
x |
x |
x |
