Хід заняття
Логічне слідування. Методи перевірки логічного слідування даної формули з формул – посилок.
Задача 1. Доведіть, що має місце наступне слідування (виводимість):
F®G, K®ØH,HÚØG |=F®ØK
Розв’язування.
Складемо
для формул F®G,
K®ØH,
HÚØG
і F®ØK
таблиці
істинності.
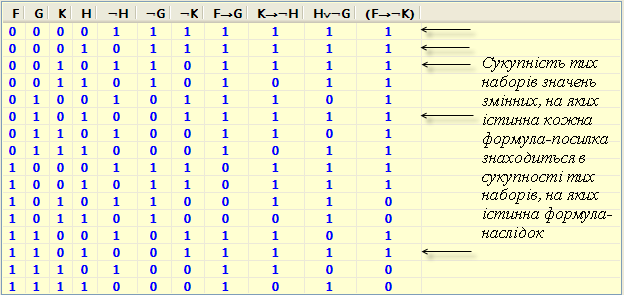
Розглянемо формули F®G, K®ØH, HÚØG і F®ØK. По таблиці істинності цих формул видно, що маємо точно п‘ять рядків, в яких перші три формули приймають значення 1, а саме перший, другий, третій, шостий і чотирнадцятий. В цих рядках четверта формула також приймає значення 1. Отже, за означенням логічного слідування
F®G, K®ØH, HÚØG |= F®ØK.
Звернемо увагу на те, що за означенням досить розглядати тільки ті рядки таблиці істинності, на яких всі посилки одночасно приймають значення 1.
Задача 2. Методом від противного з‘ясуйте, чи вірна наступна виводимість:
F®G, K®ØH, HÚØG |= F®ØK
Розв’язування.
Припустимо, що дана виводимість невірна. Тоді знайдуться такі конкретні висловлення, які перетворюють всі формули-посилки у істинні висловлення, а формулу-наслідок F→¬ К у хибне. Логічне значення формули F→¬ К буде 0 ((F→¬ К)=0), тоді, коли F приймає 1 ((F)=1), а формула ¬К примає 0 ((¬ К)= 0). Значить (К)=1. З (F→G)= 1 і (F)= 1 слідує, що (G)= 1. Далі, з (НÚ¬G)= 1 і (G)= 1 робимо висновок, що (¬Н)= 0. І нарешті, з (К→¬Н)= 1 і (¬Н)= 0 отримуємо, що (К)= 0. Прийшли до протиріччя. Тому, формула F→¬ К не може перетворюватися у хибне висловлення, якщо всі формули F→ G, F→¬ К і НÚ¬G перетворилися у істинні висловлення. Це означає, що розглянута виводимість вірна.
Задача 3. З’ясуйте, чи має місце наступне слідування:
(FÚG)®(HÙK), (KÚL)®M|=F®M
Розв’язування.
(FÚG)®(HÙK),(KÚL)®M|=F®M
По признаку логiчного слiдування, дана виводимiсть буде вiрною, якщо
наступна формула є тавтологiя:
(FÚG®HÙK)Ù(KÚL®M)®(F®M)
Для того, щоб визначити чи являється формула тавтологією можна скористатися методом істинностних таблиць або рівносильними перетвореннями. Так як формула залежить від шести пропозиційних змінних, то таблиця істинності такої формули буде мати 26=64 рядків. Тому ми скористаємося рівносильними перетвореннями:
(FÚG®HÙK)Ù(KÚL®M)®(F®M) =
Вираження iмплiкацiї через диз'юнкцiю та заперечення (21°)
(FÚG®HÙK)Ù(Ø(KÚL)ÚM)®(F®M) =
Вираження iмплiкацiї через диз'юнкцiю та заперечення (21°)
(FÚG®HÙK)Ù(Ø(KÚL)ÚM)®ØFÚM =
Вираження iмплiкацiї через диз'юнкцiю та заперечення (21°)
Ø((FÚG®HÙK)Ù(Ø(KÚL)ÚM))ÚØFÚM =
Закон де Моргана для кон'юнкцiї (9°)
Ø(FÚG®HÙK)ÚØ(Ø(KÚL)ÚM)ÚØFÚM =
Закон де Моргана для диз'юнкцiї (10°)
Ø(FÚG®HÙK)ÚØØ(KÚL)ÙØMÚØFÚM =
Закон подвiйного заперечення (1°)
Ø(FÚG®HÙK)Ú(KÚL)ÙØMÚØFÚM =
Закон комутативностi диз'юнкцiї (3°)
Ø(FÚG®HÙK)Ú(KÚL)ÙØMÚMÚØF =
Закон дистрибутивностi диз'юнкцiiї вiдносно кон'юнкцiї (8°)
Ø(FÚG®HÙK)Ú(KÚLÚM)Ù(ØMÚM)ÚØF =
Вираження одиницi через диз'юнкцiю та заперечення (18°)
Ø(FÚG®HÙK)Ú(KÚLÚM)Ù(1)ÚØF =
Закон одиницi вiдносно кон'юнкцiї (13°)
Ø(FÚG®HÙK)ÚKÚLÚMÚØF =
Вираження iмплiкацiї через диз'юнкцiю та заперечення (21°)
Ø(Ø(FÚG)ÚHÙK)ÚKÚLÚMÚØF =
Закон де Моргана для диз'юнкцiї (10°)
ØØ(FÚG)ÙØ(HÙK)ÚKÚLÚMÚØF =
Закон подвiйного заперечення (1°)
(FÚG)ÙØ(HÙK)ÚKÚLÚØFÚM =
Закон де Моргана для кон'юнкцiї (9°)
(FÚG)Ù(ØHÚØK)ÚKÚLÚØFÚM =
Закон дистрибутивностi диз'юнкцiї вiдносно кон'юнкцiї (8°)
(FÚGÚK)Ù(ØHÚØKÚK)ÚLÚØFÚM =
Вираження одиницi через диз'юнкцiю та заперечення (18°)
(FÚGÚK)Ù(ØHÚ1)ÚLÚØFÚM =
Закон одиницi вiдносно диз'юнкцiї (17°)
(FÚGÚK)Ù(1)ÚLÚØFÚM =
Закон одиницi вiдносно кон'юнкцiї (13°)
FÚØFÚGÚKÚLÚM =
Вираження одиницi через диз'юнкцiю та заперечення (18°)
1Ú(GÚKÚLÚM) =1
Закон одиницi вiдносно диз'юнкцiї (17°)
Це означає, що формула F®M логічно слідує з формул (FÚG)®(HÙK), (KÚL)®M.
Застосування теорії логічного слідування до правильних міркувань
Задача 4. З'ясуйте, чи є логічно правильним наступне міркування.
Студент піде додому (v) або залишиться в університеті (w). Він не залишиться в університеті. Отже, студент піде додому. (Буквами позначені наявні в цьому міркуванні прості висловлення.)
Розв’язування.
Запишемо це міркування символічно за допомогою зазначених у дужках букв: vÚw,Øw, v. Ці висловлення можна розглядати як значення пропозиційних формул PÚQ,ØQ, P. Істинність наслідку буде визначатися істинністю наявних висловлень, якщо PÚQ,ØQ|=P, але формула PÚQÙØQ®P є тавтологія (|=PÚQÙØQ®P). Тому можна вважати, що дане міркування логічно правильне.