
- •1.1. Атомно-молекулярная теория строения вещества
- •1.2. Масса и размеры молекул
- •1.3. Броуновское движение
- •2. Газовые законы. Идеальный и реальный газы
- •2.1. Законы Бойля-Мариотта, Гей-Люссака, Шарля
- •2.2. Уравнение состояния идеального газа
- •2.3. Плотность газов
- •2.4. Основное уравнение молекулярно-кинетической теории газов
- •2.5. Постоянная Больцмана
- •3.1. Длина свободного пробега молекул
- •3.2. Скорость газовых молекул
- •3.3. Распределение Максвелла
- •4.1. Предмет термодинамики. Постулаты термодинамики
- •4.2. Температурные шкалы. Абсолютная температура
- •4.3. Температура в молекулярно-кинетической теории
- •4.3. Температура в молекулярно-кинетической теории
- •4.4. Внутренняя энергия. Работа. Теплота
- •4.5. Первое начало термодинамики.Понятие теплоемкости
- •4.6. Применение первого начала термодинамики к описанию изопроцессов в идеальном газе
- •4.7. Первое начало термодинамики как принцип эквивалентности теплоты и работы
- •4.8. Невозможность вечного двигателя первого рода
- •4.9. Принципы работы тепловых машин
- •4.10. Цикл карно. Кпд тепловых двигателей
- •4.11. Обратимые и необратимые процессы
- •4.12. Второй закон термодинамики
- •4.13. Теорема карно
- •4.14. Энтропия. Неравенство клаузиуса. Математическое выражение второго начала термодинамики
- •4.15. Статистический смысл второго начала термодинамики
- •4.16. Энтропия и термодинамическая вероятность. Формула больцмана
- •4.17. Энтропия и беспорядок
- •4.18. О "тепловой смерти" вселенной
- •5.1. Кристаллическая решетка
- •5.2. Дефекты в кристаллах
- •5.3. Плавление и кристаллизация
- •5.4. Зависимость температуры плавления от давления
- •5.5. Испарение твердых тел (сублимация)
- •5.6. Механические свойства твердых тел
- •6.1. Силы взаимодействия между молекулами. Агрегатные состояния вещества
- •6.2. Особенности строения и теплового движения в жидкостях
- •6.3. Свойства жидкостей
- •6.4. Явления на границе жидкость–пар. Насыщенный пар
- •6.5. Кипение жидкости. Зависимость температуры кипения от давления
- •6.6. Равновесие двухфазного состояния жидкость-пар. Критическая температура
- •6.7. Водяной пар в атмосфере. Влажность
- •6.8. Поверхностное натяжение
- •6.9. Давление Лапласа под искривленной поверхностью жидкости
- •6.10. Капиллярные явления. Формула Жюрена
- •6.11. Смачивание и несмачивание на границе жидкость-жидкость и твердое тело-жидкость
- •6.12. Текучесть жидкости. Сверхтекучесть гелия
6.10. Капиллярные явления. Формула Жюрена
В жизни часто приходится иметь дело с телами, пронизанными множеством мелких каналов (бумага, пряжа, кожа, почва, дерево). Приходя в соприкосновение с водой или другими жидкостями, такие тела очень часто впитывают в себя жидкость. На этом основано действие полотенца, фитиля в лампе, питание растений. Подобные явления можно также наблюдать в очень узких стеклянных трубочках, которые называются капиллярными (от латинского слова "капилля" – волос).
Для капиллярных сосудов характерна прежде всего кривизна поверхности жидкости в них, поэтому в таких сосудах в полной мере проявляются эффекты, обусловленные избыточным давлением Лапласа. К числу таких эффектов относится капиллярный подъем.
|
Под искривленной поверхностью вогнутого мениска давление в жидкости, как это было рассмотрено выше, меньше атмосферного давления Р0 на величину давления Лапласа (рис. 6.17б).
Под действием возникшей разности давлений на уровне поверхности жидкости в широком сосуде и непосредственно под мениском в капиллярной трубочке жидкость начинает подниматься по трубочке, и будет подниматься до тех пор, пока гидростатическое давление поднявшегося столба жидкости не будет равно давлению Лапласа.
Условие равновесия жидкости в капиллярной трубочке определяется равенством
|
(6.23) |
где ρ – плотность жидкости, h – высота ее поднятия в трубочке, g – ускорение силы тяжести.
Из (6.23) следует:
|
(6.24) |
Преобразуем (6.24), выразив радиус кривизны R мениска через радиус капиллярной трубочки r (рис. 6.18).
Из рис. 6.18 следует, что
|
(6.25) |
Подставляя (6.25) в (6.24), получаем:
|
(6.26) |
|
|
|
|
|
В частном случае для жидкости, полностью
смачивающей стенки капилляра
![]() ,
формула Жюрена принимает вид:
,
формула Жюрена принимает вид:
|
(6.27) |
|
|
(6.28) |
В формуле учтено, что давление Лапласа при цилиндрическом мениске равно .
Если жидкость не смачивает капилляр, то в трубочке образуется выпуклый мениск, центр кривизны которого не вне, а внутри жидкости. В этом случае добавочное давление Лапласа направлено вниз. Уровень жидкости в капиллярной трубочке опускается ниже уровня жидкости в широкой части сосуда. Говорят, что имеет место отрицательный капиллярный подъем (рис. 6.20). Отметим еще, что формула Жюрена может быть использована для экспериментального определения коэффициента поверхностного натяжения жидкости. Для этого нужно измерить радиус капиллярной трубочки и высоту поднятия в ней жидкости.
|

 Рис.
6.17
Рис.
6.17 Рис.
6.18
Рис.
6.18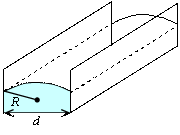 Рис.
6.19
Рис.
6.19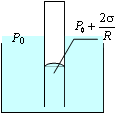 Рис.
6.20
Рис.
6.20