
- •1.1. Атомно-молекулярная теория строения вещества
- •1.2. Масса и размеры молекул
- •1.3. Броуновское движение
- •2. Газовые законы. Идеальный и реальный газы
- •2.1. Законы Бойля-Мариотта, Гей-Люссака, Шарля
- •2.2. Уравнение состояния идеального газа
- •2.3. Плотность газов
- •2.4. Основное уравнение молекулярно-кинетической теории газов
- •2.5. Постоянная Больцмана
- •3.1. Длина свободного пробега молекул
- •3.2. Скорость газовых молекул
- •3.3. Распределение Максвелла
- •4.1. Предмет термодинамики. Постулаты термодинамики
- •4.2. Температурные шкалы. Абсолютная температура
- •4.3. Температура в молекулярно-кинетической теории
- •4.3. Температура в молекулярно-кинетической теории
- •4.4. Внутренняя энергия. Работа. Теплота
- •4.5. Первое начало термодинамики.Понятие теплоемкости
- •4.6. Применение первого начала термодинамики к описанию изопроцессов в идеальном газе
- •4.7. Первое начало термодинамики как принцип эквивалентности теплоты и работы
- •4.8. Невозможность вечного двигателя первого рода
- •4.9. Принципы работы тепловых машин
- •4.10. Цикл карно. Кпд тепловых двигателей
- •4.11. Обратимые и необратимые процессы
- •4.12. Второй закон термодинамики
- •4.13. Теорема карно
- •4.14. Энтропия. Неравенство клаузиуса. Математическое выражение второго начала термодинамики
- •4.15. Статистический смысл второго начала термодинамики
- •4.16. Энтропия и термодинамическая вероятность. Формула больцмана
- •4.17. Энтропия и беспорядок
- •4.18. О "тепловой смерти" вселенной
- •5.1. Кристаллическая решетка
- •5.2. Дефекты в кристаллах
- •5.3. Плавление и кристаллизация
- •5.4. Зависимость температуры плавления от давления
- •5.5. Испарение твердых тел (сублимация)
- •5.6. Механические свойства твердых тел
- •6.1. Силы взаимодействия между молекулами. Агрегатные состояния вещества
- •6.2. Особенности строения и теплового движения в жидкостях
- •6.3. Свойства жидкостей
- •6.4. Явления на границе жидкость–пар. Насыщенный пар
- •6.5. Кипение жидкости. Зависимость температуры кипения от давления
- •6.6. Равновесие двухфазного состояния жидкость-пар. Критическая температура
- •6.7. Водяной пар в атмосфере. Влажность
- •6.8. Поверхностное натяжение
- •6.9. Давление Лапласа под искривленной поверхностью жидкости
- •6.10. Капиллярные явления. Формула Жюрена
- •6.11. Смачивание и несмачивание на границе жидкость-жидкость и твердое тело-жидкость
- •6.12. Текучесть жидкости. Сверхтекучесть гелия
6.9. Давление Лапласа под искривленной поверхностью жидкости
Форма поверхности жидкости, налитой в сосуд, определяется тремя факторами: силами взаимодействия между молекулами жидкости, силами взаимодействия между молекулами жидкости и молекулами, входящими в состав стенок сосуда, и действием силы тяжести.
Если достаточно большое количество жидкости налито в широкий сосуд, то жидкость вследствие преобладающего действия силы тяжести в этом случае имеет плоскую горизонтальную поверхность. Однако непосредственно у стенок сосуда поверхность жидкости несколько искривлена. Если молекулы жидкости, соприкасающиеся со стенкой сосуда, взаимодействуют с молекулами твердого тела сильнее, чем между собой, в этом случае жидкость стремится увеличить площадь соприкосновения с твердым телом. При этом поверхность жидкости изгибается вниз и говорят, что она смачивает стенки сосуда, в котором находится.
Если же молекулы жидкости взаимодействуют между собой сильнее, чем с молекулами стенок сосуда, то жидкость стремится сократить площадь соприкосновения с твердым телом, ее поверхность искривляется вверх, имеет место несмачивание жидкостью стенок сосуда.
|
Наличие сил поверхностного натяжения и кривизны поверхности жидкости в капиллярной трубочке ответственно за дополнительное давление под искривленной поверхностью, называемое давлением Лапласа.
|
|
(6.17) |
|
(6.18) |
Действие этой силы приходится на круговое
сечение мениска площадью
![]() (рис.
6.14). Следовательно, избыточное давление
Лапласа, обусловленное кривизной
поверхности и действием сил поверхностного
натяжения, равно
(рис.
6.14). Следовательно, избыточное давление
Лапласа, обусловленное кривизной
поверхности и действием сил поверхностного
натяжения, равно
|
(6.19) |
Можно обобщить полученную формулу на случай более сложной поверхности. В общем случае давление Лапласа определяется соотношением
|
(6.20) |
где R1 и R2 – радиусы кривизны двух взаимно перпендикулярных сечений мениска.
|
Применяя формулу Лапласа для частного
случая сферической капли
![]() ,
находим:
,
находим:
|
(6.21) |
Если поверхность мениска имеет цилиндрическую форму, то один из радиусов кривизны сечения можно считать равным бесконечности. Для этого частного случая давление Лапласа равно
|
(6.22) |
В случае мыльного пузырька дополнительное
давление, которое испытывает находящийся
внутри него газ, равно
![]() ,
так как у пузырька две поверхности –
наружная и внутренняя, каждая из которых
создает дополнительное давление Лапласа.
,
так как у пузырька две поверхности –
наружная и внутренняя, каждая из которых
создает дополнительное давление Лапласа.
Убедительной иллюстрацией существования лапласовского давления служит описанный ниже опыт.
|

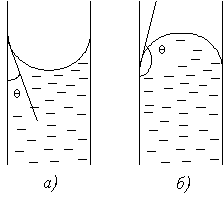 Рис.
6.13
Рис.
6.13 Рис.
6.14
Рис.
6.14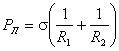 ,
,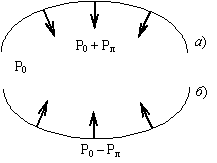 Рис.
6.15
Рис.
6.15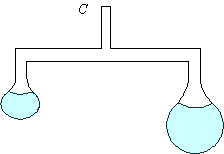 Рис.
6.16
Рис.
6.16