
- •1.1. Атомно-молекулярная теория строения вещества
- •1.2. Масса и размеры молекул
- •1.3. Броуновское движение
- •2. Газовые законы. Идеальный и реальный газы
- •2.1. Законы Бойля-Мариотта, Гей-Люссака, Шарля
- •2.2. Уравнение состояния идеального газа
- •2.3. Плотность газов
- •2.4. Основное уравнение молекулярно-кинетической теории газов
- •2.5. Постоянная Больцмана
- •3.1. Длина свободного пробега молекул
- •3.2. Скорость газовых молекул
- •3.3. Распределение Максвелла
- •4.1. Предмет термодинамики. Постулаты термодинамики
- •4.2. Температурные шкалы. Абсолютная температура
- •4.3. Температура в молекулярно-кинетической теории
- •4.3. Температура в молекулярно-кинетической теории
- •4.4. Внутренняя энергия. Работа. Теплота
- •4.5. Первое начало термодинамики.Понятие теплоемкости
- •4.6. Применение первого начала термодинамики к описанию изопроцессов в идеальном газе
- •4.7. Первое начало термодинамики как принцип эквивалентности теплоты и работы
- •4.8. Невозможность вечного двигателя первого рода
- •4.9. Принципы работы тепловых машин
- •4.10. Цикл карно. Кпд тепловых двигателей
- •4.11. Обратимые и необратимые процессы
- •4.12. Второй закон термодинамики
- •4.13. Теорема карно
- •4.14. Энтропия. Неравенство клаузиуса. Математическое выражение второго начала термодинамики
- •4.15. Статистический смысл второго начала термодинамики
- •4.16. Энтропия и термодинамическая вероятность. Формула больцмана
- •4.17. Энтропия и беспорядок
- •4.18. О "тепловой смерти" вселенной
- •5.1. Кристаллическая решетка
- •5.2. Дефекты в кристаллах
- •5.3. Плавление и кристаллизация
- •5.4. Зависимость температуры плавления от давления
- •5.5. Испарение твердых тел (сублимация)
- •5.6. Механические свойства твердых тел
- •6.1. Силы взаимодействия между молекулами. Агрегатные состояния вещества
- •6.2. Особенности строения и теплового движения в жидкостях
- •6.3. Свойства жидкостей
- •6.4. Явления на границе жидкость–пар. Насыщенный пар
- •6.5. Кипение жидкости. Зависимость температуры кипения от давления
- •6.6. Равновесие двухфазного состояния жидкость-пар. Критическая температура
- •6.7. Водяной пар в атмосфере. Влажность
- •6.8. Поверхностное натяжение
- •6.9. Давление Лапласа под искривленной поверхностью жидкости
- •6.10. Капиллярные явления. Формула Жюрена
- •6.11. Смачивание и несмачивание на границе жидкость-жидкость и твердое тело-жидкость
- •6.12. Текучесть жидкости. Сверхтекучесть гелия
6.8. Поверхностное натяжение
Отличительной особенностью жидкости является наличие у нее свободной поверхности. Молекулы, расположенные на этой поверхности, находятся в особых условиях по сравнению с молекулами остальной массы жидкости. Рассмотрим молекулу А, расположенную внутри некоторого большого объема жидкости (рис. 6.8). Эта молекула взаимодействует с окружающими ее молекулами, попадающими в так называемую сферу молекулярного действия, радиус которой порядка 10-7 см. Поскольку молекулы в жидкости расположены с равномерной плотностью, то равнодействующая всех сил, действующих на рассматриваемую молекулу, равна нулю.
|
Наличие равнодействующей силы, стремящейся втянуть молекулу внутрь жидкости, приводит к тому, что молекула, попадающая в поверхностный слой, должна совершить работу против этой силы. Совершенная при этом работа определяет дополнительный запас потенциальной энергии молекул поверхностного слоя. Очевидно, что чем больше свободная поверхность жидкости, тем большее число ее молекул обладают избыточной потенциальной энергией.
Хорошо известно, что любая система в природе стремится к минимуму потенциальной энергии. Следовательно, в поверхностном слое жидкости должна действовать сила, стремящаяся сократить ее свободную поверхность. Эта сила и есть сила поверхностного натяжения.
|
|
|
(6.15) |
где ΔS – приращение поверхности шейки.
Если бы процесс увеличения площади поверхности шейки протекал адиабатически, то совершенная над жидкостью работа на основании первого начала термодинамики была бы равна изменению внутренней энергии жидкости. Изменение внутренней энергии жидкости складывается из двух составляющих, одна из которых ΔUпов связана с изменением внутренней энергии поверхностного слоя, другая – ΔUоб с изменением объемной составляющей внутренней энергии.
Известно, что увеличение поверхности жидкости сопровождается ее охлаждением (потенциальная энергия молекул поверхностного слоя увеличивается за счет кинетической энергии молекул, находящихся внутри жидкости). Понятно поэтому, что, для того чтобы исключить влияние объемной составляющей внутренней энергии, процесс увеличения поверхности шейки должен протекать в изотермических условиях. Для выполнения этого условия к системе должно быть подведено некоторое количество теплоты Q. Подведенное количество теплоты Q исключает изменение объемной составляющей внутренней энергии, а совершенная работа А определяет изменение внутренней энергии поверхностного слоя жидкости.
Величину А называют свободной энергией поверхности, так как при сокращении поверхности жидкости она, подобно потенциальной энергии, переходит в другие формы энергии или расходуется на работу по перемещению жидкости.
Итак, на основании соотношения (6.15) коэффициент поверхностного натяжения можно определить как работу, которую нужно совершить при изотермическом увеличении поверхностного слоя жидкости на единицу площади. Или иначе эта величина равна свободной энергии единицы площади поверхностного слоя жидкости.
Экспериментальное определение величины σ показывает, что поверхностное натяжение зависит от природы жидкости, ее температуры, присутствия в ее составе поверхностно-активных веществ и свойств среды, с которой она граничит. Однако поверхностное натяжение никак не зависит от того, велика поверхность жидкости или мала, подвергалась ли до этого поверхность жидкости растяжению или нет. Это означает, что работа, которая затрачивается на то, чтобы молекула попала в поверхностный слой, не зависит от площади этого слоя.
В связи с этим стоит заметить, что поверхностный слой жидкости нельзя уподоблять тонкой упругой пленке, например, резиновой. При растяжении резиновой пленки по мере увеличения ее поверхности растягивающая сила становится все больше и больше. И, следовательно, работа по увеличению этой поверхности также возрастает. При увеличении поверхности жидкости, как было отмечено выше, такого эффекта не наблюдается.
Заметим еще, что, исходя из двух возможных подходов к определению коэффициента поверхностного натяжения, можно заключить, что эта величина в системе СИ измеряется либо в Н/м, либо в Дж/м2 (в системе СГС – соответственно в дн/см или эрг/см2).
Ниже в таблице 6.1 приведены значения коэффициентов поверхностного натяжения некоторых жидкостей.
Таблица 6.1
Жидкость |
Т, ºС |
σ, Дж/м2 |
Вода (чистая) |
20 |
0,0725 |
Раствор мыла |
20 |
0,040 |
Спирт |
20 |
0,022 |
Эфир |
25 |
0,017 |
Ртуть |
20 |
0,470 |
Золото расплавленное |
1130 |
1,102 |
Жидкий водород |
-253 |
0,0021 |
Гелий |
-269 |
0,00012 |
Из приведенных данных наглядно видно, что у легко испаряющихся жидкостей (спирт, эфир) коэффициент поверхностного натяжения более чем на порядок отличается от значения для таких жидкостей, как ртуть. Это обстоятельство отражает тот факт, что силы молекулярного взаимодействия в спирте и эфире значительно слабее, чем взаимодействие молекул ртути.
Наибольшее значение силы поверхностного натяжения обнаруживают в расплавленных металлах, наименьшее – у жидкого водорода и, особенно, у жидкого гелия. Установлено, что для разных жидкостей коэффициент поверхностного натяжения может принимать значения в интервале от единицы до двух тысяч.
Экспериментальные исследования показывают, что коэффициент поверхностного натяжения жидкости зависит от температуры. Надежно установлено, что с повышением температуры коэффициент поверхностного натяжения уменьшается. Об этом свидетельствуют результаты опытов, проведенных с жидкостями вблизи критической температуры, когда стирается различие между жидкостью и ее насыщенным паром, исчезает четкая граница раздела сред, а значение коэффициента поверхностного натяжения жидкости стремится к нулю.
Однако установить точный вид зависимости коэффициента поверхностного натяжения жидкости от температуры оказалось невозможно. Ее приблизительный вид, полученный на основании многочисленных экспериментальных данных, выражается равенством
|
(6.16) |
где ρ – плотность жидкости, μ –
молекулярный вес,
![]() .
.
Таблица 6.2
Т, ºС |
σ, Н/М |
0 |
0,0756 |
20 |
0,0725 |
50 |
0,0679 |
100 |
0,0588 |
В таблице 6.2 приведены для примера данные по температурной зависимости коэффициента поверхностного натяжения для воды. Можно считать, что вдали от критической температуры коэффициент поверхностного натяжения уменьшается по линейному закону.
Выше уже отмечалось, что коэффициент поверхностного натяжения жидкости существенно зависит от того, с какой средой граничит жидкость. Естественно ожидать, что коэффициент поверхностного натяжения на границе двух жидкостей должен быть меньше, чем на свободной поверхности жидкости. Это можно объяснить тем, что силы взаимодействия между молекулами граничащих жидкостей и молекулами каждой жидкости между собой направлены в противоположные стороны. В подтверждение отмеченной выше зависимости приводится таблица 6.3 значений коэффициента поверхностного натяжения на границе раздела двух жидких сред.
Таблица 6.3
ВЕЩЕСТВО |
σ, Н/М |
Вода-бензол |
0,0336 |
Вода-эфир |
0,0122 |
Ртуть-вода |
0,427 |
Ртуть-спирт |
0,399 |
Хорошо известно, что снижение поверхностного натяжения достигается введением в жидкость поверхностно-активных веществ, уменьшающих ее свободную поверхностную энергию (мыло, жирные кислоты). Это обусловлено тем, что силы взаимодействия между молекулами примеси и растворителя обычно не равны силам взаимодействия между молекулами чистого растворителя. Если первые из упомянутых сил меньше, чем вторые, то такие вещества называются поверхностно-активными. Так как молекулы примеси притягиваются молекулами растворителя слабее, чем молекулы самого растворителя, то молекулы растворителя из поверхностного слоя втягиваются внутрь жидкости. В результате этого в поверхностном слое увеличивается концентрация молекул примеси, вследствие чего и уменьшается поверхностное натяжение. Поверхностный слой оказывается обедненным молекулами растворителя и обогащенным молекулами примеси. Это явление носит название адсорбции. Им объясняется устойчивость жидких пленок, пены и т.д. Адсорбция является процессом, который сопровождается понижением свободной энергии поверхностного слоя жидкости. Действительно, как показывает эксперимент, коэффициент поверхностного натяжения чистой воды при комнатной температуре равен 0,0725 Дж/м2, тогда как раствор мыла в воде при тех же условиях характеризуется коэффициентом поверхностного натяжения, равным 0,040 Дж/м2.
Существование сил поверхностного натяжения экспериментально убедительно доказывается на основании многочисленных опытов с мыльными пленками.
|
При наблюдении различных явлений природы и в повседневной жизни постоянно приходится сталкиваться с проявлением сил поверхностного натяжения. Хорошо известно, что воплощение детских фантазий при строительстве сказочных дворцов возможно только тогда, когда песок будет достаточно влажным. Сухие песчинки не пристают друг к другу и из них ничего построить нельзя. Силы поверхностного натяжения очень наглядно проявляются и во время купания. Когда человек погружается с головой в воду, его волосы расходятся во все стороны. Но стоит только высунуть голову из воды, волосы сразу же лягут на голове слипшимися слоями, поскольку в этом случае поверхность воды имеет меньшую площадь, чем при раздельном расположении волос. Аналогичный эффект наблюдается при использовании художественной кисти.
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, каплях воды, разбегающихся по раскаленной плите, и мелких каплях воды на пыльной дороге. Во всех этих случаях взаимодействие между молекулами жидкости больше, чем между молекулами жидкости и молекулами тела, на поверхности которого жидкость находится.
|
Хорошо известен классический опыт Плато, описание которого приводится ниже. В сосуд, содержащий раствор спирта в воде, вливают некоторое количество прованского масла, которое в растворе спирта не растворяется. Под действием силы тяжести масло стремится разлиться по поверхности раствора в виде тонкой пленки. Такое поведение масла вполне закономерно, поскольку соответствует минимальной потенциальной энергии в поле силы тяжести.
Если далее с помощью пипетки увеличить концентрацию спирта в растворе, то можно получить раствор, плотность которого равна плотности масла. При этом сила тяжести, действующая на масло, оказывается равной действующей на него силе Архимеда. Таким образом, удается исключить действие силы тяжести. При этом условии силами, определяющими поведение жидкости (масла), становятся силы поверхностного натяжения. В результате действия этих сил вместо пленки, растекающейся по поверхности раствора, масло собирается в каплю, имеющую правильную сферическую форму.
Очень эффектные картины в поведении жидкости наблюдают космонавты во время полетов. В состоянии невесомости силы поверхностного натяжения проявляются в чистом виде, поэтому капельки воды в космическом корабле принимают форму шара.
Это интересно

 Рис.
6.8
Рис.
6.8 Рис.
6.9
Рис.
6.9 Рис.
6.10
Рис.
6.10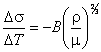 ,
, Рис.
6.11
Рис.
6.11 Рис.
6.12
Рис.
6.12